一. 綜述

真隨機數(shù)發(fā)生器（TRNG）是硬件加密的重要組成部分，它與偽隨機數(shù)生成器（PRNG）不同，是利用抖動等不可控因素作為隨機數(shù)的熵源，所生成的隨機數(shù)具有真正的隨機性。本文講述一種新穎的熵提取方法，用來提高基于抖動的真隨機數(shù)發(fā)生器在FPGA上的吞吐量。即通過利用超高速的進位邏輯基元，提高熵提取的效率，從而提高吞吐量。下面以Spartan-6 FPGA上基于環(huán)形振蕩器的真正隨機數(shù)發(fā)生器為例說明設(shè)計步驟和技術(shù)。這種設(shè)計方法同在FPGA上基于抖動的高效TRNG相比，所需要的熵提取累積時間縮短了3個數(shù)量級，而且僅僅用了67個slice就實現(xiàn)了14.3 Mbps的吞吐量，并且這項研究提供了對安全性的正式評估。

二. 介紹

早期FPGA的TRNG實現(xiàn)不提供熵模型。早期研究出的發(fā)生器通過使用諸如NIST 和DIEHARD 等統(tǒng)計測試進行驗證，但他們?nèi)狈Π踩缘恼皆u估。在FPGA上僅有少數(shù)TRNG設(shè)計提供數(shù)學(xué)模型和熵估計。而我們的新方法從累積的定時抖動中提取高效的熵。不是通過以高能量或面積為代價增加轉(zhuǎn)換數(shù)量來提高吞吐量，而是專注于改善單次轉(zhuǎn)換的熵提取。我們的主要想法是基于TRNG吞吐量與采樣信號的定時分辨率的平方成比例增加的事實。由于這個原因，即使定時分辨率的適度改進也會導(dǎo)致積累時間和比例吞吐量增益的大幅降低。

在Xilinx FPGA上，兩種類型的slices包含一個進位鏈（carrychain）基元，可用于生成分支，加法器或乘法器。該基元由連接到觸發(fā)器的四個延遲級組成，并可配置為抽頭延遲線。可以通過專用路徑連接來自同一列上的相鄰slice的進位鏈，以形成更大的延遲線。這種配置可用于采樣時間精度較高的信號，并已用于實現(xiàn)高分辨率時間數(shù)字轉(zhuǎn)換器。通過利用進位鏈進行熵提取，我們的TRNG實現(xiàn)了更小的占位面積，?更大的吞吐量。并且提供了此TRNG的安全評估。

三. TRNG的實現(xiàn)方案

TRNG評估的早期方法包括收集隨機數(shù)據(jù)并運行一系列統(tǒng)計測試，如NIST和DIEHARD測試。這種黑盒子方法的一個主要缺陷是所有PRNG即使產(chǎn)生完全確定性輸出也可以輕松通過統(tǒng)計測試。即使用TRNG設(shè)計人員驗證自己的設(shè)計，這種方法也是有問題的。例如，設(shè)計師可能認為，隨機性是由熱抖動引起的，而實際上它來自不穩(wěn)定的電源。在這種情況下，如果TRNG與穩(wěn)壓器一起使用，它可能會產(chǎn)生非常弱的抖動。雖然統(tǒng)計測試可用于初始分析或健全性檢查，但它們不能代替正式的安全評估。TRNG的正式安全評估需要TRNG的數(shù)學(xué)模型和熵評估。AIS-31為TRNG的設(shè)計和評估提供了一個框架。AIS-31認證的要求之一是熵源的隨機模型和生成熵的下邊界的估計。

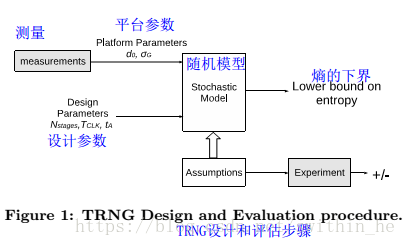
隨機模型用于描述隨時間演變的概率系統(tǒng)。它比物理模型（如晶體管模型）更簡單，因為它只考慮影響隨機性的過程。這種類型的模型用于描述在電路中產(chǎn)生熵的過程，例如抖動累積或從亞穩(wěn)狀態(tài)解析的過程。圖1顯示了TRNG的框圖。隨機模型必須基于明確陳述和實驗可驗證的假設(shè)。該模型的目標是為平臺參數(shù)（例如LUT延遲或噪聲參數(shù)）和設(shè)計參數(shù)（例如環(huán)形振蕩器的數(shù)量或采樣頻率）的不同值提供熵估計。所獲得的隨機模型基于輸入?yún)?shù)（平臺和設(shè)計參數(shù)）來計算最小熵。設(shè)計流程的下一個階段是通過實驗獲取平臺參數(shù)。之后，需要確定最佳設(shè)計參數(shù)。這可以通過使用隨機模型和平臺參數(shù)的測量值來計算設(shè)計參數(shù)的不同值的熵來完成。然后可以調(diào)整設(shè)計參數(shù)直到達到指定的熵界限。統(tǒng)計分析在評估的最后階段完成。

四.實驗架構(gòu)

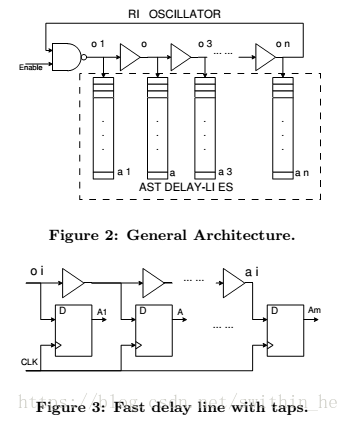
我們的架構(gòu)基于高精度采樣不穩(wěn)定信號的概念，從而比標準方法提取更多的熵。這種方法非常有效，因為吞吐量方面的增益與精度的改進平方成正比。在這個架構(gòu)中，熵源和熵提取器作為為獨立的塊來實現(xiàn)。系統(tǒng)中的所有隨機性由信號邊緣的時間不確定性產(chǎn)生。振蕩器信號首先通過抽頭延遲線傳播，取樣并根據(jù)捕獲的數(shù)據(jù)片段確定信號邊緣的位置。數(shù)字化數(shù)據(jù)被傳播到熵提取器，然后在輸出端產(chǎn)生一個隨機位。

熵源和數(shù)字化模塊如圖2所示。熵源實現(xiàn)為一個自由運行的n級振蕩器，使用一個NAND門和多個緩沖器。數(shù)字化模塊由連接到每個延遲元件輸出的快速抽頭延遲線組成。這些延遲線正在執(zhí)行噪聲信號的時間 - 數(shù)字轉(zhuǎn)換。

圖3顯示了單抽頭延遲線的內(nèi)部結(jié)構(gòu)。該行由m個快速緩沖器和一組連接到其輸出的觸發(fā)器組成。轉(zhuǎn)換的時序分辨率等于分接延遲線單級的延遲。在時鐘上升沿之后，每個緩沖器的輸出數(shù)據(jù)在觸發(fā)器中被捕獲。這些數(shù)據(jù)反映了振蕩器的內(nèi)部狀態(tài)。為了捕捉振蕩器的完整狀態(tài)，必須選擇作為抽頭延遲線的大小的參數(shù)m，抽頭延遲線必須被選擇為使得抽頭線的延遲大于熵源中最慢元素的延遲。否則，信號邊沿可以通過任何線路檢測不到。這也是為了提供魯棒性，因為振蕩器元件的延遲以及轉(zhuǎn)換的時間步長可能因溫度或電壓變化而變化，并且在最壞情況下必須檢測到信號邊緣。由于采樣期間的時序違規(guī)，一些觸發(fā)器可能會被驅(qū)動到亞穩(wěn)狀態(tài)，從而可能產(chǎn)生“氣泡”碼。

延遲線的預(yù)期輸出是連續(xù)運行'1'，然后運行'0'或運行'0'由運行'1'休止。在大多數(shù)情況下，如圖4（a）所示，信號沿只會在一個延遲線中捕獲。熵提取器用于解碼此邊的位置，它必須能夠處理兩種效果：代碼中的多邊和邊界。由于單個抽頭線的延遲大于振蕩器元件的延遲，因此會出現(xiàn)多個邊緣。如果信號邊緣看起來靠近延遲線的末端，則信號可以通過下一個振蕩器元件傳播，這導(dǎo)致在下一行的開始處出現(xiàn)第二個邊緣。熵提取器總是解碼第一個邊緣而忽略第二個邊緣，見圖4（b）。代碼中的“氣泡”（圖4（c））使用優(yōu)先級解碼器進行過濾。

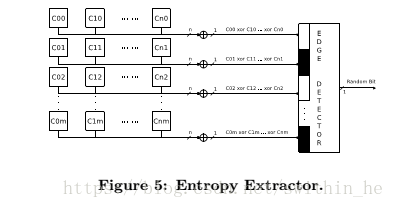
熵提取器的體系結(jié)構(gòu)如圖5所示。抽頭延遲線（由Ci，j表示，其中i是行數(shù)，j是一行中的位數(shù)）分為兩個階段進行處理。首先，所有行均按位進行著色，產(chǎn)生一個m位向量。該矢量被饋送到邊緣檢測器，該邊緣檢測器輸出優(yōu)先級編碼器的LSB，使得奇數(shù)位置被編碼為'0'，甚至位置被編碼為'1'。

所提出的架構(gòu)的設(shè)計參數(shù)是：n環(huán)形振蕩器的級數(shù)，m - 快速延遲線中的級數(shù)和tA-抖動累積時間。

五. 隨機模型

在本節(jié)中，我們提供對擬議設(shè)計的正式安全評估。我們從關(guān)于FPGA平臺的假設(shè)開始，為二元概率計算開發(fā)一個簡單的隨機模型。主要目標是提供每比特熵的下限，以及確定最佳設(shè)計參數(shù)，如階段數(shù)和抖動累積時間。

5.1 假設(shè)

我們通過以下假設(shè)開始初始安全分析：
? 每個LUT的延遲由一個確定性分量d0，LUT和一個隨機分量Δd組成。隨機分量受局部熱噪聲的影響。這個隨機分量可以用正態(tài)分布N（0，σLUT2）來模擬，其中σLUT是標準偏差。
? 除白噪聲之外的噪聲源可能會對可變分量產(chǎn)生影響。這些包括閃爍噪聲，由電源變化引起的全局噪聲和攻擊者的操縱影響（例如通過EM輻射）。這些噪音在我們的模型中沒有量化，因此我們將始終假設(shè)最差情況值。
? 抖動實現(xiàn)的白噪聲分量是相互獨立的。
? 通過快速延遲線傳播的噪聲信號使用等距bin tstep進行采樣。

前三個假設(shè)是眾所周知的并且通過實驗驗證。最后一個需要針對特定的實現(xiàn)平臺進行實驗性調(diào)查。

5.2二進制概率計算

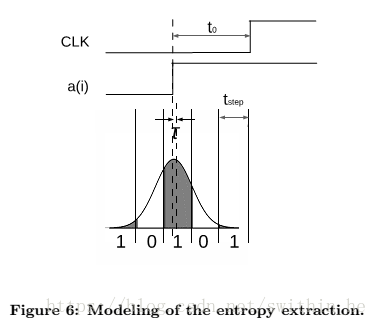
TRNG按以下方式運行。振蕩器運行時間tA，之后采樣信號被激活。在此期間，來自每個延遲元件輸出的信號通過快速延遲線傳播。由于振蕩器是自由運行的，所以抖動隨時間積累。只要延遲線足夠長（m·tstep> d0，LUT），就可以保證在延遲線中至少捕獲一個噪聲信號邊緣。圖6顯示了熵提取模型。描述采樣邊緣和噪聲信號之間的相對熱抖動使用高斯分布。由于抖動實現(xiàn)是獨立的，在時間tA之后積累的熱抖動的標準偏差與轉(zhuǎn)換事件的數(shù)量的平方根成比例：

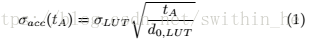
噪聲信號以精確的tstep采樣并且TDC的鄰近狀態(tài)使用不同的比特進行編碼。1和0的概率等于曲線下的面積。

這些概率取決于采樣邊緣和噪聲信號邊緣的最可能位置之間的偏移時間，如圖6所示。我們將τ定義為有噪聲信號邊緣與最接近采樣bin中間的間隔，如圖所示 在圖中：

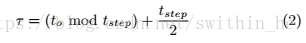
在不失一般性的情況下，我們可以假設(shè)這個bin被解碼為1.然后，二元概率由下式給出：

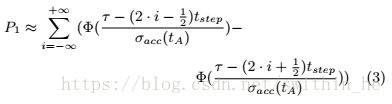
其中Φ是高斯分布的累積概率函數(shù)：

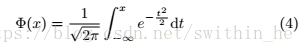
5.3熵下界

二進制概率取決于偏移時間τ。τ的確切值取決于累積時間，序列中樣本的數(shù)量，還取決于低頻噪聲和確定性噪聲。由于這些因素不可預(yù)測也不可控，所以應(yīng)該使用最壞情況值來估計熵的下限。香農(nóng)熵然后由下式給出：

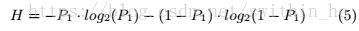
圖7顯示了取決于τ的香農(nóng)熵。當(dāng)τ= 0時達到下限。

5.4模型使用

所提出的隨機模型可用于根據(jù)平臺參數(shù)和設(shè)計參數(shù)來估計熵的下限。該模型由一組方程組成，這些方程組可以作為一個Matlab函數(shù)實現(xiàn)，該函數(shù)根據(jù)平臺和設(shè)計參數(shù)產(chǎn)生熵下限。平臺參數(shù)是實現(xiàn)平臺的物理參數(shù)，它們應(yīng)該通過測量來確定。此設(shè)計的相關(guān)平臺參數(shù)為：d0，LUT - 單個LUT的平均延遲，帶有快速延遲線的tstep-bin以及由單個轉(zhuǎn)換事件生成的熱噪聲σLUT。

一旦平臺參數(shù)已知，該模型用于確定不同設(shè)計參數(shù)值的熵的下限。設(shè)計參數(shù)為：環(huán)形振蕩器中的級數(shù)，快速延遲線中的m級，fCLK系統(tǒng)時鐘頻率，tA - 抖動累積時間（也可以表示為NA - 系統(tǒng)時鐘周期數(shù)）和可選的下采樣因子k。下采樣可用于通過將k個鄰近倉組合成一個倉來提高快速延遲線中的時間 - 數(shù)字轉(zhuǎn)換的線性度。隨機模型用于確定不同設(shè)計參數(shù)值的熵值，從而可以探索不同的設(shè)計折衷。

因此，TRNG的設(shè)計過程由以下四個步驟組成：
步驟1：測量相關(guān)的平臺參數(shù)。
步驟2：基于隨機模型和獲得的平臺參數(shù)確定最優(yōu)設(shè)計參數(shù)。
第3步：FPGA實現(xiàn)。

步驟4：對生成的比特進行統(tǒng)計評估。

5.5 后處理

生成的位可以使用后處理來改進。后處理是一種壓縮技術(shù)，以降低吞吐量為代價提高了每比特熵。Xor后處理是一個簡單的方法，具有緊湊的硬件實現(xiàn)。它由連續(xù)產(chǎn)生的位組成，從而將吞吐量降低np倍。提出的隨機模型可以用來估計生成數(shù)的最大偏差，定義為：

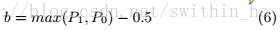
使用壓縮率np的后處理序列的偏差為：

然后可以計算新的熵值。

六.實施

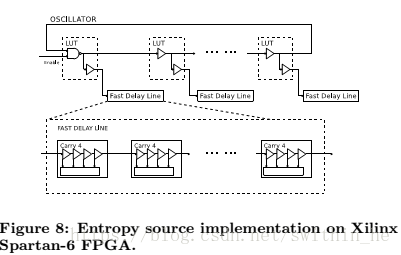
使用Xilinx Spartan-6 FPGA實現(xiàn)。熵源和數(shù)字轉(zhuǎn)換器的實現(xiàn)方法如圖8所示。環(huán)形振蕩器的階段使用LUT實現(xiàn)，快速延遲線使用進位鏈基元實現(xiàn)。在Spartan-6上，一半的片包含這些進位原語。這些切片位于偶數(shù)列中。通過連接來自相同列中相鄰切片的進位基元來形成長進位鏈。振蕩器的延遲級放置在快速延遲線正下方的切片中。這些是我們在實現(xiàn)中使用的唯一布局約束。設(shè)計的其余部分是自動合成和實現(xiàn)的。

6.1平臺參數(shù)

感興趣的平臺參數(shù)是LUT延遲d0，LUT，熱抖動的標準偏差σG，LUT和TDC轉(zhuǎn)換的時間步長tstep，即進位鏈中單個元件的延遲。
??????? LUT延遲是通過實現(xiàn)一個環(huán)形振蕩器并在固定時間內(nèi)計算轉(zhuǎn)換次數(shù)來確定的。發(fā)現(xiàn)d0，LUT = 480ps。
抽頭行延遲步驟通過捕獲長進位鏈中的振蕩器輸出并計數(shù)時鐘周期的級數(shù)來確定。結(jié)果大約是tstep = 17ps。
熱抖動測量必須非常小心地執(zhí)行，因為此參數(shù)非常重要。從歷史上看，有很多論文高估了這個參數(shù)，為了獲得準確的結(jié)果還有幾個挑戰(zhàn)需要克服。進行測量的最可靠的方法是，因為可以在引腳，封裝和示波器上過濾出熱噪聲。根據(jù)文獻[4]給出的電路模型，測量時間需要很短（1μs或更短），否則低頻噪聲占主導(dǎo)地位。測量必須有差別地進行，以便考慮全球噪聲源，例如電源的不穩(wěn)定性。我們提出了一種簡單的方法來確定使用進位鏈邏輯的FPGA上的抖動。兩個相同的環(huán) -?

振蕩器被實現(xiàn)并放置得彼此靠近。振蕩器啟用20ns，并使用基于carry4原語的快速抽頭延遲線捕獲輸出。捕獲的數(shù)據(jù)然后發(fā)送到PC進行分析。通過觀察兩個振蕩器的信號邊沿之間的差異來確定累積抖動。抖動的標準偏差從1000個測量結(jié)果中估算出來。得到的結(jié)果表明σG，LUT≈2ps。

6.2 設(shè)計參數(shù)

環(huán)形振蕩器的級數(shù)n不在熵模型中。為了實現(xiàn)最緊湊的實現(xiàn)，應(yīng)該選擇此參數(shù)的值盡可能小。我們選擇n = 3的值，因為這是最短的環(huán)形振蕩器，我們可以可靠地測量頻率和抖動參數(shù)。
????????快速延遲線m的級數(shù)必須選擇為始終檢測到信號邊沿，這種情況發(fā)生在m> d0，LUT / tstep。對于我們的平臺參數(shù)，這個條件變成m> 29。由于每個carry4原語有4個元素，m必須是4的倍數(shù)。最初，我們嘗試使用8個進位原語（m = 32），但測量結(jié)果表明信號邊緣是沒有在0.8％的案例中被捕獲。這可能是由于d0是平均延遲值，而一些LUT可能較慢。為了提供更好的魯棒性，我們決定使用9個carry4階段（m = 36），測量結(jié)果表明邊緣總是被捕獲。沒有進一步增加米的好處。

要克服的挑戰(zhàn)之一是進位鏈的非線性，即不同的倉具有不同的寬度。在[6]中進行的一項研究表明，這種非線性的主要原因是不平衡的時鐘樹。同樣的文章還建議通過使用跨越一個時鐘區(qū)域的進位鏈來提高線性度。在Spartan-6上，時鐘區(qū)跨越16行。由于我們的設(shè)計僅使用9個carry4階段，因此可以設(shè)置放置約束以確保所有9個階段都處于同一時鐘區(qū)域。時間 - 數(shù)字轉(zhuǎn)換的非線性的另一個原因是carry4原語的內(nèi)部結(jié)構(gòu)以及過程變化的影響。這可以通過使用k = 4的下采樣來改善，這導(dǎo)致了更寬的分箱和更高的tA要求。為了探索設(shè)計空間，我們實現(xiàn)了多種版本的TRNG，使用k = 1和k = 4。積累時間tA必須是10ns的倍數(shù)，因為平臺時鐘頻率是100MHz。我們針對兩種版本的TRNG探索不同tA值的設(shè)計空間。

6.對比

使用隨機模型和獲得的平臺參數(shù)，我們將熵提取方法與基本TRNG在同一平臺上使用的方法進行比較。基本TRNG由一個由系統(tǒng)鎖定采樣的自由振蕩器組成。抖動累積過程與我們的模型中所描述的完全相同，但是熵提取是不同的，因為有噪聲的信號是在定時 - 等于環(huán)形振蕩器的半周期的情況下采樣的。在最好的情況下，環(huán)形振蕩器僅使用一個LUT來實現(xiàn)，這會導(dǎo)致tstep，RO = d0，LUT。

由于吞吐量與采樣精度的平方成比例地進行縮放，因此我們在k = 1時獲得的吞吐量改進是：

這幾乎是3個數(shù)量級。

對于k = 4，改進因子是49.8。

七. 結(jié)果

我們在Xilinx Spartan-6 FPGA上實現(xiàn)了兩種版本的TRNG。兩個版本的參數(shù)值都是n = 3和m = 36。一個版本使用down-sampling（k = 4），另一個版本不使用down-sampling（k = 1）。對于k = 1的TRNG占據(jù)包括熵源和熵提取器的67個slices。TRNG版本k = 4更小，因為它只占用40個slices。
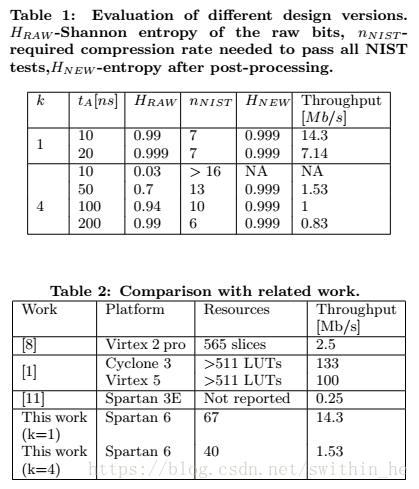
表1顯示了不同設(shè)計參數(shù)的統(tǒng)計評估和吞吐量結(jié)果。生成的數(shù)據(jù)使用異或后處理進行壓縮，nNIST是通過所有統(tǒng)計測試所需的最小壓縮率。根據(jù)模型計算壓縮前后的每比特熵（HRAW和HNEW）。壓縮后的吞吐量報告在最后一列。

表2總結(jié)了與相關(guān)工作的比較。除[1]外，我們的設(shè)計實現(xiàn)了比所有TRNG更高的吞吐量。然而，[1]中的TRNG僅使用了511個LUT用于熵源，在Xilinx平臺上最多為128個slice（本文中未報告確切的利用率結(jié)果）。我們的熵源是一個環(huán)形振蕩器，它只消耗3個slices，完整的設(shè)計消耗40個slices。

在這項工作中，我們提出了一種用于FPGA上高吞吐量，真隨機數(shù)發(fā)生器的新型熵提取技術(shù)。這種技術(shù)依靠進位邏輯原語對累積抖動進行有效采樣。該技術(shù)以Xilinx Spartan-6 FPGA上實現(xiàn)的高吞吐量TRNG為例進行說明。顯示了所有設(shè)計和評估步驟，包括平臺參數(shù)測量，探索設(shè)計空間和運行統(tǒng)計評估。最快的TRNG實施占用67個slices，達到14.3Mb / s的吞吐量。最緊湊的實現(xiàn)消耗40個slices并實現(xiàn)1.53Mb / s的吞吐量。未來的工作將側(cè)重于在不同的實現(xiàn)平臺上應(yīng)用所提出的方法，并開發(fā)嵌入式測試以進行實時評估。

編輯：黃飛

?