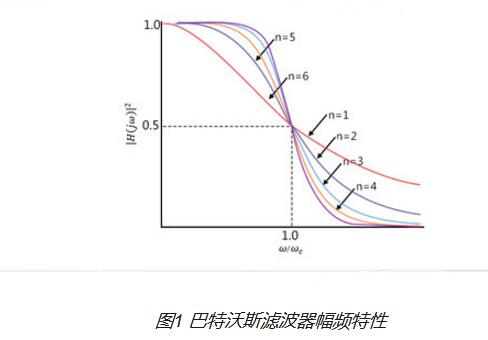
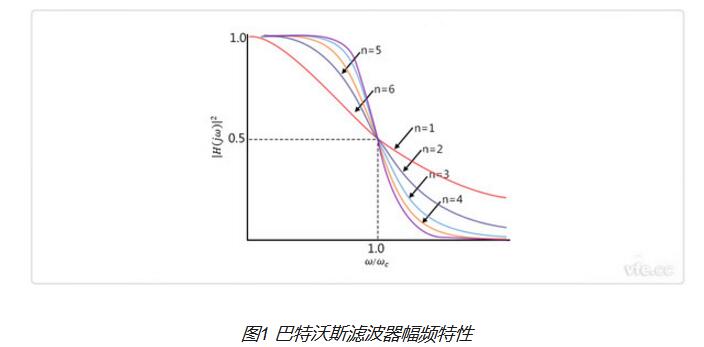
巴特沃斯濾波器是電子濾波器的一種。巴特沃斯濾波器的特點是通頻帶的頻率響應曲線最平滑。這種濾波器最先由英國工程師斯蒂芬·巴特沃斯（Stephen Butterworth）在1930年發(fā)表在英國<無線電工程>期刊的一篇論文中提出的。

巴特沃斯濾波器的次數(shù)

根據(jù)給定的參數(shù)設計模擬濾波器，然后進行變數(shù)變換，求取數(shù)字濾波器的方法，稱為濾波器的間接設計。做為數(shù)字濾波器的設計基礎的模擬濾波器，稱之為原型濾波器。這里，我們首先介紹的是最簡單最基礎的原型濾波器，巴特沃斯低通濾波器。由于IIR濾波器不具有線性相位特性，因此不必考慮相位特性，直接考慮其振幅特性。

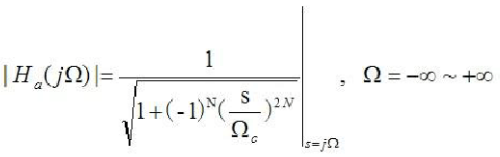
在這里，N是濾波器的次數(shù)，Ωc是截止頻率。從上式的振幅特性可以看出，這個是單調(diào)遞減的函數(shù)，其振幅特性是不存在紋波的。設計的時候，一般需要先計算跟所需要設計參數(shù)相符合的次數(shù)N。首先，就需要先由阻帶頻率，計算出阻帶衰減

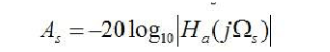
將巴特沃斯低通濾波器的振幅特性，直接帶入上式，則有

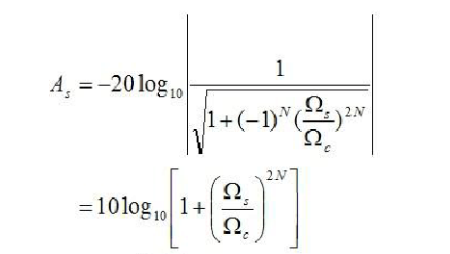
最后，可以解得次數(shù)N為

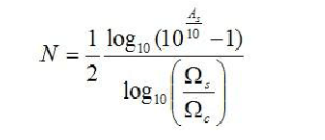
當然，這里的N只能為正數(shù)，因此，若結果為小數(shù)，則舍棄小數(shù)，向上取整。

巴特沃斯濾波器的傳遞函數(shù)

巴特沃斯低通濾波器的傳遞函數(shù)，可由其振幅特性的分母多項式求得。其分母多項式

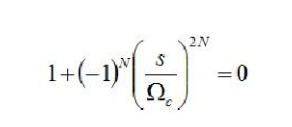
根據(jù)S解開，可以得到極點。這里，為了方便處理，我們分為兩種情況去解這個方程。當N為偶數(shù)的時候，

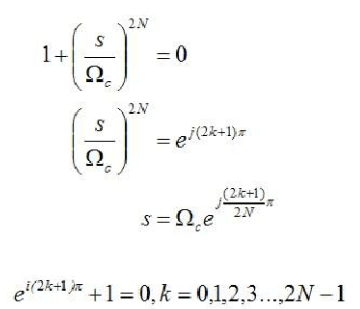
這里，使用了歐拉公式。同樣的，當N為奇數(shù)的時候，

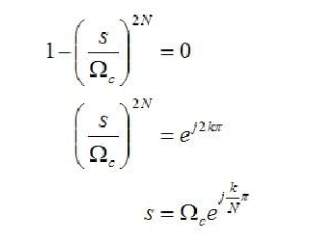
同樣的，這里也使用了歐拉公式。歸納以上，極點的解為

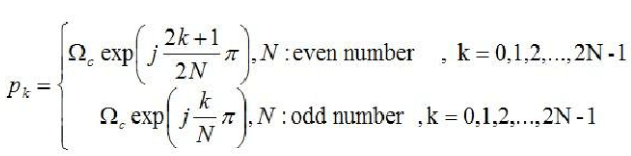
上式所求得的極點，是在s平面內(nèi)，在半徑為Ωc的圓上等間距的點，其數(shù)量為2N個。為了使得其IIR濾波器穩(wěn)定，那么，只能選取極點在S平面左半平面的點。選定了穩(wěn)定的極點之后，其模擬濾波器的傳遞函數(shù)就可由下式求得。

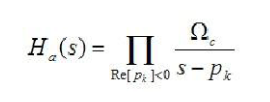
巴特沃斯濾波器的實現(xiàn)（C語言）

首先，是次數(shù)的計算。次數(shù)的計算，我們可以由下式求得。

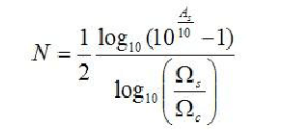
其對應的C語言程序為

N = Ceil（0.5*（ log10 （ pow （10， Stopband_attenuation/10） - 1） /

log10 （Stopband/Cotoff） ））;

然后是極點的選擇，這里由于涉及到復數(shù)的操作，我們就聲明一個復數(shù)結構體就可以了。最重要的是，極點的計算含有自然指數(shù)函數(shù)，這點對于計算機來講，不是太方便，所以，我們將其替換為三角函數(shù)，

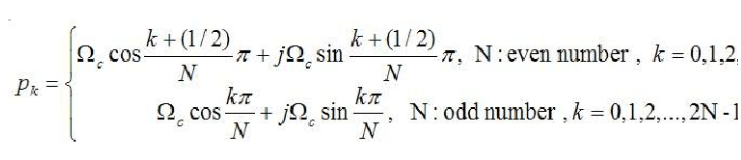
這樣的話，實部與虛部就還可以分開來計算。其代碼實現(xiàn)為

typedef struct

{

double Real_part;

double Imag_Part;

} COMPLEX;

COMPLEX poles［N］;

for（k = 0;k <= （（2*N）-1） k++）

{

if（Cotoff*cos（（k+dk）*（pi/N）） < 0）

{

poles［count］.Real_part = -Cotoff*cos（（k+dk）*（pi/N））;

poles［count］.Imag_Part= -Cotoff*sin（（k+dk）*（pi/N））;

count++;

if （count == N） break;

}

}

計算出穩(wěn)定的極點之后，就可以進行傳遞函數(shù)的計算了。傳遞的函數(shù)的計算，就像下式一樣

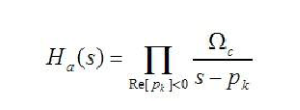
這里，為了得到模擬濾波器的系數(shù)，需要將分母乘開。很顯然，這里的極點不一定是整數(shù)，或者來說，這里的乘開需要做復數(shù)運算。其復數(shù)的乘法代碼如下，

int Complex_Multiple（COMPLEX a，COMPLEX b，

double *Res_Real，double *Res_Imag）

{

*（Res_Real） = （a.Real_part）*（b.Real_part） - （a.Imag_Part）*（b.Imag_Pa

rt）;

*（Res_Imag）= （a.Imag_Part）*（b.Real_part） + （a.Real_part）*（b.Imag_Par

t）;

return （int）1;

}

有了乘法代碼之后，我們現(xiàn)在簡單的情況下，看看其如何計算其濾波器系數(shù)。我們做如下假設

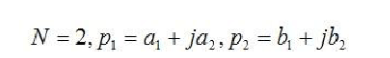
這個時候，其傳遞函數(shù)為

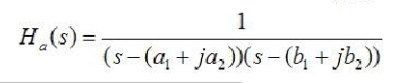
將其乘開，其大致的關系就像下圖所示一樣。

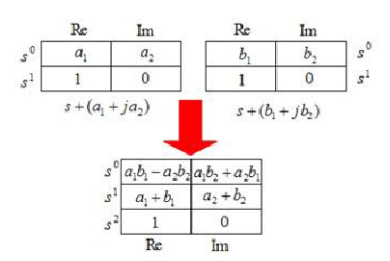
Res［0］.Real_part = poles［0］.Real_part;

Res［0］.Imag_Part= poles［0］.Imag_Part;

Res［1］.Real_part = 1;

Res［1］.Imag_Part= 0; 5.

for（count_1 = 0;count_1 < N-1;count_1++）

{

for（count = 0;count <= count_1 + 2;count++）

{

if（0 == count）

{

Complex_Multiple（Res［count］， poles［count_1+1］，

&（Res_Save［count］.Real_part），

&（Res_Save［count］.Imag_Part））;

}

else if（（count_1 + 2） == count）

{

Res_Save［count］.Real_part += Res［count - 1］.Real_part;

Res_Save［count］.Imag_Part += Res［count - 1］.Imag_Part;

}

else

{

Complex_Multiple（Res［count］， poles［count_1+1］，

&（Res_Save［count］.Real_part），

&（Res_Save［count］.Imag_Part））;

1 Res_Save［count］.Real_part += Res［count - 1］.Real_part;

Res_Save［count］.Imag_Part += Res［count - 1］.Imag_Part;

}

}

*（b+N） = *（a+N）;