??Matlab中生成向量的三種方法

　 ? ?在Matlab中，如何才能生成向量，生成向量的方法又有多少種？相信這是每一個初學(xué)者都想知道的問題。這里小編將向大家詳細(xì)介紹Matlab中生成向量的三種方法。

　　方法一：直接輸入法

　　1這是最簡單的向量生成法，我們只需按照向量的格式輸入就可以了。如我們要生成向量A=［7，8，9，4，5，6］;這里A是個一維向量，其中的分量是7，8，9，4，5，6。

　　方法二：冒號生成法

　　1這種方法適用于元素與元素之間存在等距步長（差值）的情況，即當(dāng)元素間呈等差數(shù)列時可以使用。冒號生成法，其語法格式為：

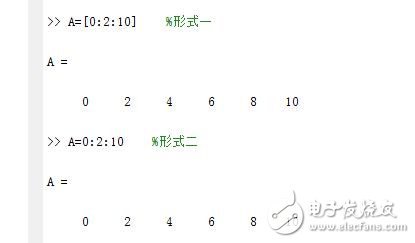
　　1.向量名=［第一個元素?cái)?shù)值：步長：最后一個元素的數(shù)值］；

　　2.向量名=第一個元素?cái)?shù)值：步長：最后一個元素的數(shù)值

　　如我們要生成向量A=［0，2，4，6，8，10］，如圖所示：

　　方法三：線性等分法

　　這種方法與冒號生成法有點(diǎn)相似，都是利用元素間的等差值來實(shí)現(xiàn)，但與冒號生成法又有些不同，不同的是線性等分法是利用函數(shù)的形式來實(shí)現(xiàn)的。語法格式如下：

　　向量名=linespace（第一個元素?cái)?shù)值：最后一個元素?cái)?shù)值：向量位數(shù)）;

　　如我們要將0～10的所有元素劃分為一組6維的向量：

　　matlab中如何定義向量

　　1、預(yù)置（preallocation）是編寫MATLAB程序比較重要的一個因素，在數(shù)組比較大的時候，是否進(jìn)行預(yù)置程序運(yùn)行時間相差幾十倍甚至幾百幾千倍都很常見。所以使用

　　A=zero（1，n）;

　　或者A=zero（n，1）;

　　進(jìn)行預(yù)置通常很重要（如果n不大倒可以不做）。

　　2、提高M(jìn)ATLAB程序效率的另一個要點(diǎn)是向量化（Vectorization）代替顯式循環(huán)。向量化表達(dá)式主要使用點(diǎn)運(yùn)算操作符。例如，就樓主的問題而言，可以很簡單的寫成

　　A=x.^（1:n）;

　　省略了 for 循環(huán)，對于程序效率也會有很大提升。關(guān)于點(diǎn)運(yùn)算更詳細(xì)的介紹，可以看一下參考資料的鏈接中我以前回答的問題。

　　matlab向量定義方法：

　　1.向量的普通定義方法

　　向量的常見格式有以下三種：

　　v1=1:N; %格式1

　　v2=x1:dx:x2 ； %格式2

　　v3=x4：-dx:x3; %格式3

　　參數(shù)說明：

　　v1，v2，v3是返回的向量名。格式1中的向量的步長等于1，向量v1的最小值和最大值分貝是1和N，此種格式常用于循環(huán)指標(biāo)的定義。格式2中的設(shè)定向量間隔步長是dx，向量的v2的最小值和最大值分別是x1和x2.格式3中的向量的步長等于-dx，它是一個負(fù)數(shù)，而向量的最大值和最小值分別是x4和x3。所有的返回向量都是行向量。在v1的定義的步長缺省，這是步長等于1，而向量的v2的生成語句中，步長等于dx.

　　2.用linspace函數(shù)定義向量的方法

　　函數(shù)linspace可以生成兩個數(shù)之間的等間隔向量，其調(diào)用格式如下：

　　v1=linspace（x1，x2）; %格式1

　　v2=linspace（x1，x2，N）; %格式2

　　參數(shù)說明：

　　v1和v2是返回的函數(shù)名。在格式1中，x1和x2是向量的兩個端點(diǎn)，向量元素個數(shù)是100。在格式2中，x1和x2表示向量的兩個端點(diǎn)，N用于指定的元素個數(shù)。當(dāng)N是一個小數(shù)的時候，matlab將把N進(jìn)行向0取整，即fix（N）;當(dāng)N時負(fù)數(shù)的時候，返回的向量v2將等于x1.同時x1和x2的大小關(guān)系人任意時，matlab自動調(diào)整正負(fù)步長，x1作為向量的起點(diǎn)，x2作為向量的終點(diǎn)。所有返回的向量都是行向量。

　　當(dāng)linspace的輸入?yún)?shù)N缺省時，生成的向量長度是100，我們可以任意指定。

　　3.用logspace函數(shù)定義向量的方法

　　函數(shù)logspace可以用來產(chǎn)生一個對數(shù)向量，其調(diào)用的格式如下：

　　v1=logspace（x1，x2）; %格式1

　　v2=logspace（x1，x2，n）; %格式2

　　參數(shù)說明：v1和v2是返回的對數(shù)向量。x1和x2用來控制端點(diǎn)，返回向量的兩個端點(diǎn)的大小為10^1和10^2.格式1中的向量長度是50.格式2中的n用于指定向量的元素個數(shù)。函數(shù)logspace的計(jì)算過程是先得到x1和 x2之間的等間距向量，然后計(jì)算10^（linspace（x1，x2，n）），因此函數(shù)logspace得到的向量不是等間距向量，取對數(shù)后才是等距的。

　　4.用randperm函數(shù)來定義向量

　　函數(shù)randperm可以用于產(chǎn)生一個元素為從1到N的隨機(jī)自然序列，其調(diào)用的格式如下：

　　rand（‘state’，s）

　　v=randperm（N）;

　　參數(shù)說明：

　　s用于設(shè)定隨機(jī)數(shù)的狀態(tài)，這樣程序每次執(zhí)行的結(jié)果都是一樣的，我們可以改變S的值以便取到不同的隨機(jī)數(shù)。N用來定義隨機(jī)向量的中的最大整數(shù)。