為什么要校準

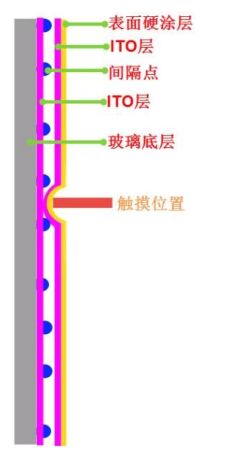
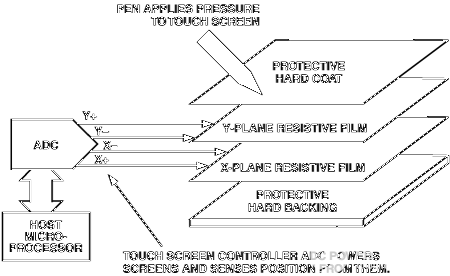
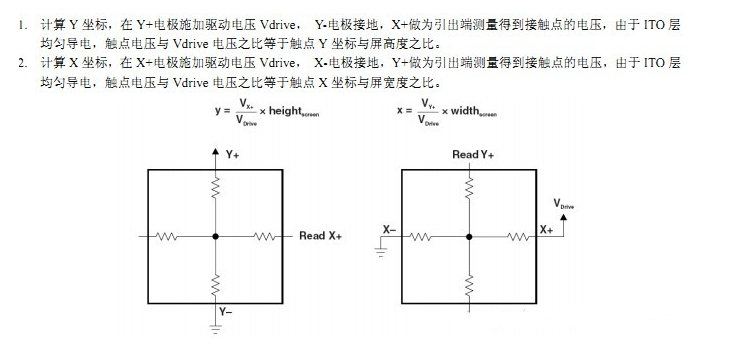
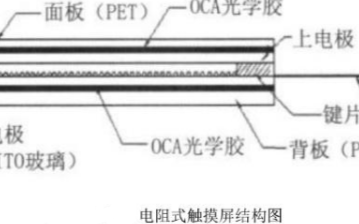
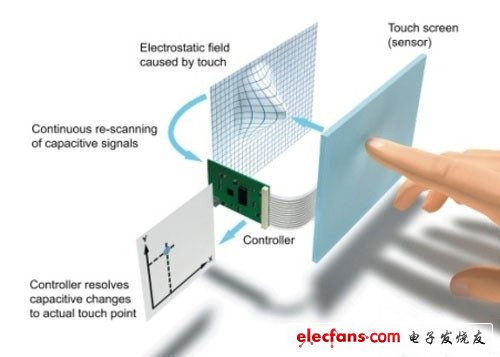
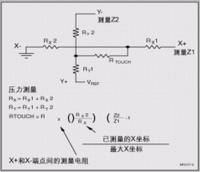
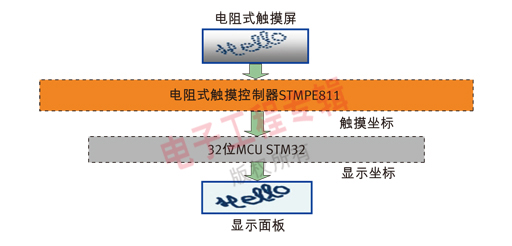
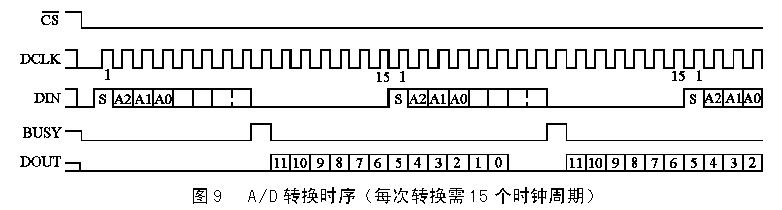
　　簡單來說，電阻式觸摸屏就是一種傳感器，它利用壓力感應進行控制，將矩形區域中觸摸點（X，Y）的物理位置轉換為代表X坐標和Y坐標的電壓電阻式觸摸屏的主要部分是一塊與顯示器表面非常配合的電阻薄膜屏，這是一種多層的復合薄膜，它以一層玻璃或硬塑料平板作為基層，表面涂有一層導電層（透明的導電電阻），上面再蓋一層經過硬化處理光滑防擦的塑料層它的內表面也涂有一層透明導電層層，在他們之間有許多細小的（小于1/1000英寸）的透明隔離點把兩層導電層隔開絕緣當手指觸摸屏幕時，兩層導電層在觸摸點位置就有了接觸，電阻發生變化，其中一面導電層接通Y軸方向的5V均勻電壓場，使得偵測層的電壓由零變為非零，控制器偵測到這個接通后，進行A/D轉換，并將得到的電壓值與5V相比即可得觸摸點的Y軸坐標，同理也能得出X軸的坐標，然后再根據模擬鼠標的方式運作。

　　這就是所有電阻技術觸摸屏共同的最基本原理由壓力感應得到坐標值的并不能達到100%的精度，它存在著誤差。由于誤差的存在，在觸摸屏上所繪制的圖形和液晶屏上的圖形，對應點的集合會有所偏差在觸摸屏上點擊某一按鈕或選擇某項功能時，內置的軟件便無法對觸摸屏上的點擊做出正確響應，而觸摸屏具有離散性，任意兩個觸摸點密度都不能完全一致，所以幾乎所有帶阻性觸摸屏的設備在出廠前均要經過一定的校準校準是一種圖形重建的過程，即將圖形經過變換，換算出與液晶屏相一致的點集合，現有的校準算法主要是用來改善上述中的固有誤差。

　　電阻觸摸屏校準算法基本原理

　　1、基本概念

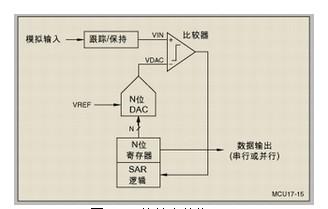
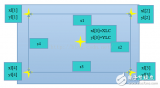
　　我們先引入兩個概念，物理坐標和邏輯坐標。物理坐標指觸摸屏上點的實際位置，通常以液晶上點的個數來度量。邏輯坐標指這點被觸摸時A/D轉換后的坐標值。如圖1，我們假定液晶最左下角為坐標軸原點A，在液晶上任取一點B（十字線交叉中心），B在X方向距離A10個點，在Y方向距離A20個點，則這點的物理坐標為（10，20）。如果我們觸摸這一點時得到的X向A/D轉換值為100，Y向A/D轉換值為200，則這點的邏輯坐標為（100，200）。

　　2、兩點校準法

　　兩點校準法即為取觸摸屏成對角線的兩個點來校準觸摸屏。下面以取觸摸屏左上角和右下角這兩個點為例進行說明

　　1）先觸摸并獲取觸摸屏左上角坐標（lefttop_x，lefttop_y）

　　2）再觸摸并獲取觸摸屏右下角坐標（rightbottom_x，rightbottom_y）

　　3）計算觸摸屏在水平方向和垂直方向的比率

　　Ratio_x=（rightbottom_x-lefttop_x）/觸摸屏寬度

　　Ratio_y=（rightbottom_y-lefttop_y）/觸摸屏高度

　　4）假設觸摸屏當前點的坐標為（X，Y）

　　當前點X坐標=X*Ratio_x+lefttop_x

　　當前點Y坐標=Y*Ratio_y+lefttop_y

　　3、三點校準法

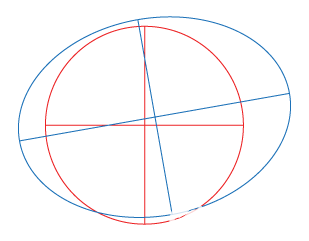
　　觸摸屏常和點陣式液晶顯示（LCD）屏疊加在一起配套使用，構成一個矩形的實際物理平面;而由用戶觸摸的觸摸點集合經過A/D轉換器，得到具體顯示坐標的集合，這個集合構成了一個邏輯平面。由于存在誤差，這兩個平面并不重合，校準的作用就是要將邏輯平面映射到物理平面上，即得到觸點在液晶屏上的位置坐標。校準算法的中心思想也就是要建立這樣一個映射函數現有的校準算法大多是基于線性校準，即首先假定物理平面和邏輯平面之間的誤差是線性誤差，由旋轉和偏移形成。如果已知觸摸屏上一點A，其物理坐標為（xa，ya），相應的顯示坐標為（xa’，ya’），根據假定的線性關系，可以得到：

　　Xa’=k1*xa+k2*ya+k3---------2-1

　　Ya’=k4*ya+k5ya+k6----------2-2

　　只要能夠求出線性變換的參數（k1，k2…。）就可以來校正從觸摸屏坐標得到顯示坐標，顯然要求參數，至少需要三個點的坐標，那么我們在觸摸屏上取三個點（注意：不要取邊界點，并且三點的覆蓋面要大）

　　Xa’=k1*xa+k2*ya+k3---------2-1

　　Ya’=k4*ya+k5ya+k6----------2-2

　　Xb’=k1*xb+k2*yb+k3---------2-1

　　Yb’=k4*yb+k5yb+k6----------2-2

　　Xc’=k1*xc+k2*yc+k3---------2-1

　　Yc’=k4*yc+k5yc+k6----------2-2

　　通過高數上的各種算法，求出

　　Divider=（Xa’–Xc’）*（Yb’–Yc’）-（Xb’–Xc’）*（Ya’–Yc’）

　　（Xa-Xc）*（Yb-Yc）-（Xb-Xc）*（Ya-Yc）

　　k1=---------------------------------------------------

　　Divider

　　（Xa’–Xc’）*（Xb-Xc）-（Xa-Xc）*（Xb’–Xc’）

　　k2=-------------------------------------------------------------

　　Divider

　　Ya’*（Xc’*Xb–Xb’*Xc）+Yb’*（Xa*Xc’–Xc’*Xa）+Yc’*（Xb’*Xa–Xa’*Xb）

　　K3=--------------------------------------------------------------------------------------------------------

　　Divider

　　（Ya-Yc）*（Yb’–Yc’）-（Yb-Yc）*（Ya’–Yc’）

　　k4=----------------------------------------------------------

　　Divider

　　（Xa’-Xc’）*（Yb-Yc）-（Ya-Yc）*（Xb’–Xc’）

　　k5=----------------------------------------------------------

　　Divider

　　Ya’*（Xc’*Yb–Xb’*Yc）+Yb’*（Xa’*Yc–Xc’*Ya）+Yc’*（Xb’*Ya–Xa’*Yb）

　　K6=-----------------------------------------------------------------------------------------------

　　Divider

　　通過這幾個參數，就可以算出物理坐標與顯示坐標的對應關系。