小波變換概念

　　小波變換（wavelet transform，WT）是一種新的變換分析方法，它繼承和發(fā)展了短時(shí)傅立葉變換局部化的思想，同時(shí)又克服了窗口大小不隨頻率變化等缺點(diǎn)，能夠提供一個(gè)隨頻率改變的“時(shí)間-頻率”窗口，是進(jìn)行信號(hào)時(shí)頻分析和處理的理想工具。

　　它的主要特點(diǎn)是通過變換能夠充分突出問題某些方面的特征，能對(duì)時(shí)間（空間）頻率的局部化分析，通過伸縮平移運(yùn)算對(duì)信號(hào)（函數(shù)）逐步進(jìn)行多尺度細(xì)化，最終達(dá)到高頻處時(shí)間細(xì)分，低頻處頻率細(xì)分，能自動(dòng)適應(yīng)時(shí)頻信號(hào)分析的要求，從而可聚焦到信號(hào)的任意細(xì)節(jié)，解決了Fourier變換的困難問題，成為繼Fourier變換以來在科學(xué)方法上的重大突破。

　　多尺度概念

　　1、所謂多尺度是指在RBF網(wǎng)中，采用了不同核函數(shù)方差的節(jié)點(diǎn)的作用是不同的，擁有大的核函數(shù)方差的節(jié)點(diǎn)所起的作用要大一些，因而就更傾向于代表訓(xùn)練集的整體信息。

　　2、多尺度是指GEM在基本架構(gòu)一致的情況下，根據(jù)不同分辨率構(gòu)成GEM中尺度模式、GEM區(qū)域模式及GEM全球模式、GEM低分辨模式。

　　3、當(dāng)aj0》1時(shí)稱為多尺度，從相容性條件得到離散小波函數(shù)ψj，k（t）的表達(dá)式為ψj，k（t）=a-j20ψt-kaj0b0aj0=a-j20ψ（a-j0t-kb0）（6）而離散化小波變換系數(shù)則可表示為Cj。

　　小波變換多尺度是什么意思

　　小波變換有兩個(gè)因子：一個(gè)是時(shí)移因子，另一個(gè)就是尺度因子。尺度因子a，a》1表示伸展，a 《1表示收縮。一般去根號(hào)a，目的是保證能量守恒。得到的小波信號(hào)是細(xì)節(jié)信號(hào)，小波變換被譽(yù)為顯微鏡。

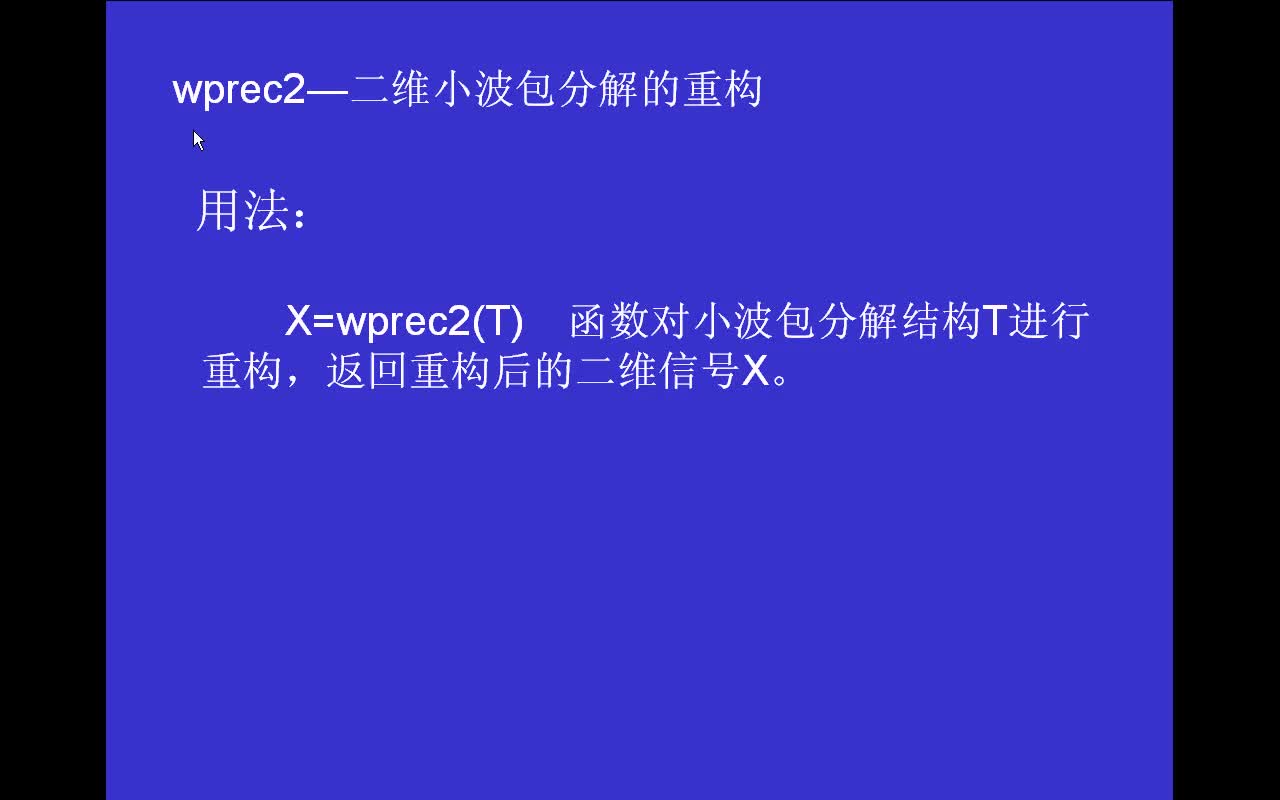
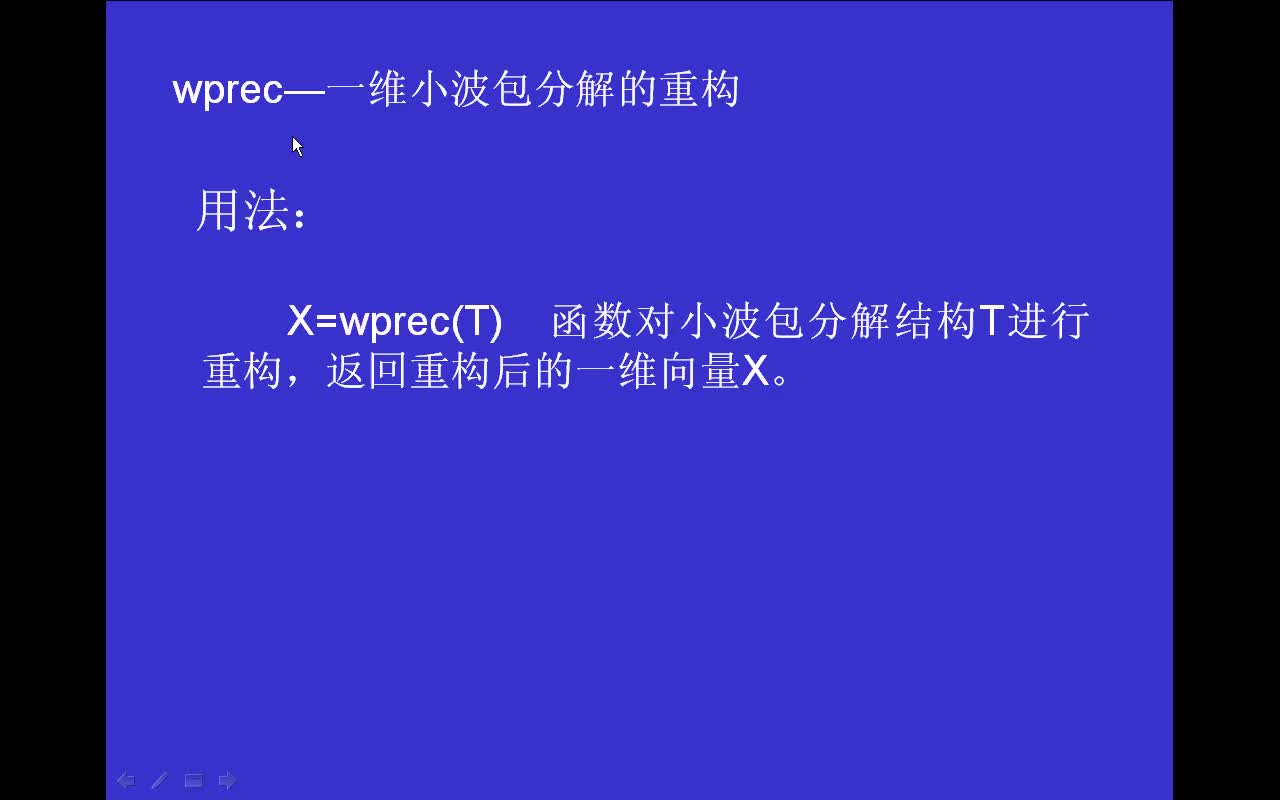
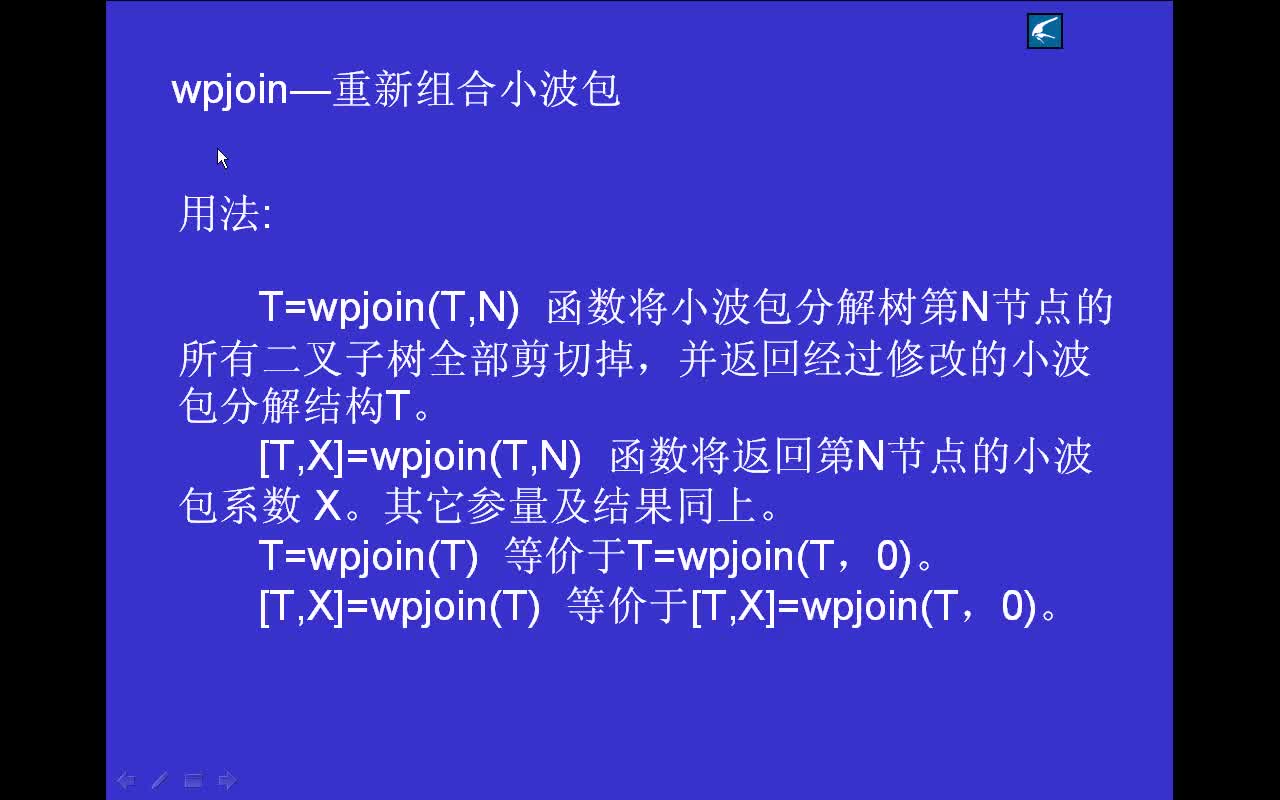
　　小波變換多尺度分解

　　一、從小波分析到多尺度幾何分析

　　小波分析取在從多學(xué)科領(lǐng)域中取得巨大成功的一個(gè)關(guān)鍵原因在于它比傅里葉分析能更“稀疏”地表示一維分段光滑或者有界變差函數(shù)。遺憾的是，小波分析在一維時(shí)所具有的優(yōu)異特性并不能簡(jiǎn)單的推廣到二維或更高維。這是因?yàn)橐痪S小波張成的可分離小波（Separable wavelet）只具有有限的方向，不能“最優(yōu)”表示含線或者面奇異的高維函數(shù)，但事實(shí)上具有線或面奇異的函數(shù)在高維空間中非常普遍，例如，自然物體光滑邊界使得自然圖像的不連續(xù)性往往體現(xiàn)為光滑曲線上的奇異性，而并不僅僅是點(diǎn)奇異。換句話說，在高維情況下，小波分析并不能充分利用數(shù)據(jù)本身特有的幾何特征，并不是最優(yōu)的或者說“最稀疏”的函數(shù)表示方法；而繼小波分析之后發(fā)展起來的多尺度幾何分析（Multiscale Geometric Analysis，MGA）發(fā)展的目的和動(dòng)力正是要致力于發(fā)展一種新的高維函數(shù)的最優(yōu)表示方法，為了檢測(cè)、表示、處理某些高維空間數(shù)據(jù)，這些空間的主要特點(diǎn)是：其中數(shù)據(jù)的某些重要特征集中體現(xiàn)于其低維子集中（如曲線、面等）。比如，對(duì)于二維圖像，主要特征可以由邊緣所刻畫，而在3-D圖像中，其重要特征又體現(xiàn)為絲狀物（filaments）和管狀物（tubes）。

　　由一維小波張成的二維小波基具有正方形的支撐區(qū)間，不同的分辨率下，其支撐區(qū)間為不同尺寸大小的正方形。二維小波逼近奇異曲線的過程最終表現(xiàn)為用“點(diǎn)”來逼近線的過程。在尺度j，小波支撐區(qū)間的邊長(zhǎng)近似為2-j，幅值超過2-j的小波系數(shù)的個(gè)數(shù)至少為O（2j）階，當(dāng)尺度變細(xì)時(shí)，非零小波系數(shù)的數(shù)目以指數(shù)形式增長(zhǎng)，出現(xiàn)了大量不可忽略的系數(shù)，最終表現(xiàn)為不能“稀疏”表示原函數(shù)。因此，我們希望某種變換在逼近奇異曲線時(shí)，為了能充分利用原函數(shù)的幾何正則性，其基的支撐區(qū)間應(yīng)該表現(xiàn)為“長(zhǎng)條形”，以達(dá)到用最少的系數(shù)來逼近奇異曲線。基的“長(zhǎng)條形”支撐區(qū)間實(shí)際上是“方向”性的一種體現(xiàn)，也稱為這種基具有“各向異性（anisotropy）”。我們希望的這種變換就是“多尺度幾何分析”。

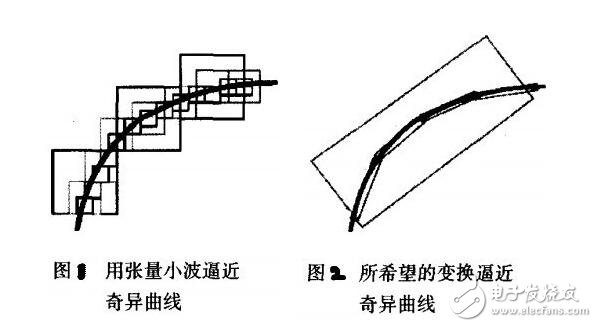
　　圖像的多尺度幾何分析方法分為自適應(yīng)和非自適應(yīng)兩類，自適應(yīng)的方法一般先進(jìn)行邊緣檢測(cè)再利用邊緣信息對(duì)原函數(shù)進(jìn)行最優(yōu)表示，實(shí)際上是邊緣檢測(cè)和圖像表示方法的結(jié)合，此類方法以Bandelet和Wdgelet為代表；非自適應(yīng)的方法并不要先驗(yàn)地知道圖像本身的幾何特征，而是直接將圖像在一組固定的基或框架上進(jìn)行分解，這就擺脫了對(duì)圖像自身結(jié)構(gòu)的依賴，其代表為Ridgelet、Curvelet和Contourlet變換。

　　二、幾種多尺度幾何分析

　　1、脊波（Ridgelet）變換

　　脊波（Ridgelet）理論由EmmanuelJ Candès于1998年在其博士論文中提出，這是一種非自適應(yīng)的高維函數(shù)表示方法，具有方向選擇和識(shí)別能力，可以更有效地表示信號(hào)中具有方向性的奇異特征。脊波變換首先對(duì)圖像進(jìn)行Radon變換，即把圖像中的一維奇異性比如圖像中的直線映射成Randon域的一個(gè)點(diǎn)，然后用一維小波進(jìn)行奇異性的檢測(cè)，從而有效地解決了小波變換在處理二維圖像時(shí)的問題。然而自然圖像中的邊緣線條以曲線居多，對(duì)整幅圖像進(jìn)行Ridgelet分析并不十分有效。為了解決含曲線奇異的多變量函數(shù)的稀疏逼近問題，1999年，Candes又提出了單尺度脊波（MonoscaleRidgelet）變換，并給出了其構(gòu)建方法。另一種方法是對(duì)圖像進(jìn)行分塊，使每個(gè)分塊中的線條都近似直線，再對(duì)每個(gè)分塊進(jìn)行Ridgelet變換，這就是多尺度Ridgelet。脊波變換對(duì)于具有直線奇異的多變量函數(shù)有良好的逼近性能，也就是說對(duì)于紋理（線奇異性）豐富的圖像，Ridgelet可以獲得比小波更加稀疏的表示；但是對(duì)于含曲線奇異的多變量函數(shù)，其逼近性能只相當(dāng)于小波變換，不具有最優(yōu)的非線性逼近誤差衰減階。

　　2、曲波（Curvelet）變換

　　由于多尺度Ridgelet分析冗余度很大，Candès和Donoho于1999年在Ridgelet變換的基礎(chǔ)上提出了連續(xù)曲波（Curvelet）變換，即第一代Curvelet變換中的Curvelet99； 2002年，Strack、Candès和Donoho提出了第一代Curvelet變換中的Curvelet02。第一代Curvelet變換實(shí)質(zhì)上由Ridgelet理論衍生而來，是基于Ridgelet變換理論、多尺度Ridgelet變換理論和帶通濾波器理論的一種變換。單尺度脊波變換的基本尺度是固定的，而Curvelet變換則不然，其在所有可能的尺度上進(jìn)行分解，實(shí)際上Curvelet變換是由一種特殊的濾波過程和多尺度脊波變換（Multiscale Ridgelet Transform）組合而成：首先對(duì)圖像進(jìn)行子帶分解；然后對(duì)不同尺度的子帶圖像采用不同大小的分塊；最后對(duì)每個(gè)分塊進(jìn)行Ridgelet分析。如同微積分的定義一樣，在足夠小的尺度下，曲線可以被看作為直線，曲線奇異性就可以由直線奇異性來表示，因此可以將Curvelet變換稱為“Ridgelet變換的積分”。

　　第一代Curvelet的數(shù)字實(shí)現(xiàn)比較復(fù)雜，需要子帶分解、平滑分塊、正規(guī)化和Ridgelet分析等一系列步驟，而且Curvelet金字塔的分解也帶來了巨大的數(shù)據(jù)冗余量，因此Candès等人于2002年又提出了實(shí)現(xiàn)更簡(jiǎn)單、更便于理解的快速Curvelet變換算法，即第二代Curvelet （FastCurvelet transform）。第二代Curvelet與第一代Curvelet在構(gòu)造上己經(jīng)完全不同。第一代Curvelet的構(gòu)造思想是通過足夠小的分塊將曲線近似到每個(gè)分塊中的直線來看待，然后利用局部的Ridgelet分析其特性，而二代的Curvelet和Ridgelet理論并沒有關(guān)系，實(shí)現(xiàn)過程也無需用到Ridgelet，二者之間的相同點(diǎn)僅在于緊支撐、框架等抽象的數(shù)學(xué)意義。2005年，Candès和Donoho提出了兩種基于第二代Curvelet變換理論的快速離散Curvelet變換實(shí)現(xiàn)方法，分別是：非均勻空間抽樣的二維FFT算法（Unequally-Spaced FastFourier Transform，USFFT）和Wrap算法（Wrapping-BasedTransform）。對(duì)于Curvelet變換，可在網(wǎng)上下載Matlab程序包Curvlab；Curvlab包里有Curvelet的快速離散算法的Matlab程序和C++程序。

　　3、輪廓波（Contourlet）變換

　　2002年，MN Do和Martin Vetterli提出了一種“真正”的圖像二維表示方法：Contourlet變換，也稱塔型方向?yàn)V波器組（Pyramidal Directional Filter Bank， PDFB）。Contourlet變換是利用拉普拉斯塔形分解（LP）和方向?yàn)V波器組（DFB）實(shí)現(xiàn)的另一種多分辨的、局域的、方向的圖像表示方法。

　　Contourlet變換繼承了Curvelet變換的各向異性尺度關(guān)系，因此，在一定意義上，可以認(rèn)為是Curvelet變換的另一種快速有效的數(shù)字實(shí)現(xiàn)方式。Contourlet基的支撐區(qū)間是具有隨尺度變化長(zhǎng)寬比的“長(zhǎng)條形”結(jié)構(gòu)，具有方向性和各向異性，Contourlet系數(shù)中，表示圖像邊緣的系數(shù)能量更加集中，或者說Contourlet變換對(duì)于曲線有更“稀疏”的表達(dá)。Contourlet變換將多尺度分析和方向分析分拆進(jìn)行，首先由LP（Laplacian pyramid）變換對(duì)圖像進(jìn)行多尺度分解以“捕獲”點(diǎn)奇異，接著由方向?yàn)V波器組（Directional Filter Bank， DFB）將分布在同方向上的奇異點(diǎn)合成為一個(gè)系數(shù)。Contourlet變換的最終結(jié)果是用類似于輪廓段（Contour segment）的基結(jié)構(gòu)來逼近原圖像，這也是所以稱之為Contourlet變換的原因。而二維小波是由一維小波張量積構(gòu)建得到，它的基缺乏方向性，不具有各向異性。只能限于用正方形支撐區(qū)間描述輪廓，不同大小的正方形對(duì)應(yīng)小波的多分辨率結(jié)構(gòu)。當(dāng)分辨率變得足夠精細(xì)，小波就變成用點(diǎn)來捕獲輪廓。

　　4、條帶波（Bandelet）變換

　　2000年，ELe Pennec和Stephane Mallat在文獻(xiàn)《EL Pennec， S Mallat. Image compression with geometrical wavelets［A］.In Proc. OfICIP’ 2000［C］。 Vancouver， Canada， September，2000.661-664》中提出了Bandelet變換。Bandelet變換是一種基于邊緣的圖像表示方法，能自適應(yīng)地跟蹤圖像的幾何正則方向。Pennec和Mallat認(rèn)為：在圖像處理任務(wù)中，若是能夠預(yù)先知道圖像的幾何正則性并充分予以利用，無疑會(huì)提高圖像變換方法的逼近性能。Pennec和Mallat首先定義了一種能表征圖像局部正則方向的幾何矢量線；再對(duì)圖像的支撐區(qū)間S進(jìn)行二進(jìn)剖分S=∪iΩi，當(dāng)剖分足夠細(xì)時(shí)，每一個(gè)剖分區(qū)間Ωi中最多只包含圖像的一條輪廓線（邊緣）。

　　在所有不包含輪廓線的局部區(qū)域Ωi，圖像灰度值的變化是一致正則的，因此，在這些區(qū)域內(nèi)不定義幾何矢量線的方向。而對(duì)于包含輪廓線的局部區(qū)域，幾何正則的方向就是輪廓的切線方向。根據(jù)局部幾何正則方向，在全局最優(yōu)的約束下，計(jì)算區(qū)域Ωi上矢量場(chǎng)τ（x1，x2）的矢量線，再沿矢量線將定義在Ωi的區(qū)間小波進(jìn)行Bandelet化（bandeletization）以生成Bandelet基，以能夠充分利用圖像本身的局部幾何正則性。Bandelet化的過程實(shí)際上是沿矢量線進(jìn)行小波變換的過程，此即所謂的彎曲小波變換（Warped wavelet transform）。于是，所有剖分區(qū)域Ωi上的Bandelet的集合構(gòu)成了一組L2（S）上的標(biāo)準(zhǔn)正交基。

　　Bandelet變換根據(jù)圖像邊緣效應(yīng)自適應(yīng)地構(gòu)造了一種局部彎曲小波變換，將局部區(qū)域中的曲線奇異改造成垂直或者水平方向上的直線奇異，再用普通的二維張量小波處理，而二維張量小波基恰恰能有效的處理水平、垂直方向上的奇異。于是，問題的關(guān)鍵歸結(jié)為對(duì)圖像本身的分析，即如何提取圖像本身的先驗(yàn)信息，怎樣剖分圖像，局部區(qū)域中如何“跟蹤”奇異方向等等。然而，在自然圖像中，灰度值的突變不總是對(duì)應(yīng)著物體的邊緣，一方面，衍射效應(yīng)使得圖像中物體的邊緣可能并不明顯地表現(xiàn)出灰度的突變；另一方面，許多時(shí)候圖像的灰度值劇烈變化，并不是由物體的邊緣而是由于紋理的變化而產(chǎn)生的。

　　所有基于邊緣的自適應(yīng)方法需要解決的一個(gè)共同的問題是如何確定圖像中灰度值劇烈變化的區(qū)域?qū)?yīng)的是物體邊緣還是紋理的變化，實(shí)際上這是一個(gè)非常困難的問題。大部分基于邊緣的自適應(yīng)算法在實(shí)際應(yīng)用中，當(dāng)圖像出現(xiàn)較復(fù)雜的幾何特征時(shí)，如Lena圖像，在逼近誤差的意義下，性能并不能超過可分離的正交小波分析。在圖像的低比特率編碼中，用來表示非零系數(shù)所在位置的開銷遠(yuǎn)遠(yuǎn)大于用來表示非零系數(shù)值的開銷。Bandelet同小波相比有兩個(gè)優(yōu)勢(shì)：（1）充分利用幾何正則性，高頻子帶能量更集中，在相同的量化步驟下，非零系數(shù)相對(duì)減少；（2）得益于四叉樹結(jié)構(gòu)和幾何流信息，Bandelet系數(shù)可以重新排列，編碼時(shí)系數(shù)掃描方式更靈活。說明Bandelet變換在圖像壓縮中的潛在優(yōu)勢(shì)。

　　構(gòu)造Bandelet變換的中心思想是定義圖像中的幾何特征為矢量場(chǎng)，而不是看成普通的邊緣集合。矢量場(chǎng)表示了圖像空間結(jié)構(gòu)的灰度值變化的局部正則方向。Bandelet基并不是預(yù)先確定的，而是以優(yōu)化最終的應(yīng)用結(jié)果來自適應(yīng)地選擇具體的基的組成。Pennec和Mallat給出了Bandelet變換的最優(yōu)基快速尋找算法，初步實(shí)驗(yàn)結(jié)果表明，與普通的小波變換相比，Bandelet在去噪和壓縮方面體現(xiàn)出了一定的優(yōu)勢(shì)和潛力。

　　5、楔波（Wedgelet）變換

　　在多尺度幾何分析工具中，Wedgelet變換具有良好的“線”和“面”的特性。

　　Wedgelet是DavidL.Donoho教授在研究從含噪數(shù)據(jù)中恢復(fù)原圖像的問題時(shí)提出的一種方向信息檢測(cè)模型。Wedgelet變換是一種簡(jiǎn)明的圖像輪廓表示方法。使用多尺度Wedgelet對(duì)圖像進(jìn)行分段線性表示，能夠根據(jù)圖像內(nèi)容自動(dòng)確定分塊大小，較好地捕捉圖像中的線和面的特征。克服了滑動(dòng)窗口方法存在的不足。

　　多尺度Wedgelet變換由兩部分組成：多尺度Wedgelet分解和多尺度Wedgelet表示。多尺度Wedgelet分解將圖像劃分成不同尺度的圖像塊，并將每個(gè)圖像塊投影成各個(gè)允許方位的Wedgelet；多尺度Wedgelet表示則根據(jù)分解結(jié)果，選擇圖像的最佳劃分，并為每個(gè)圖像塊選擇出最優(yōu)的Wedgelet表示，從而完成圖像的區(qū)域分割。

　　什么是Wedgelet？說白了，就是在一個(gè)圖像子塊（dyadic square）畫條線段，把它分成兩個(gè)楔塊，每一個(gè)楔塊用唯一的灰度值表示。線的位置，兩個(gè)灰度值，就近似刻畫了這個(gè)子塊的性質(zhì)。

　　6、小線（Beamlet）變換

　　小線變換（BeamletsTransform）是斯坦福大學(xué)的David L.Donoho教授1999年首次提出的，已經(jīng)得到了初步的應(yīng)用。由小線變換引入的小線分析（Beamlets Analysis）也是一種多尺度分析，但又不同于小波分析的多尺度概念，可以理解為小波分析多尺度概念的延伸，小線分析以各種方向、尺度和位置的小線段為基本單元來建立小線庫，圖像與庫中的小線段積分產(chǎn)生小線變換系數(shù)，以小線金字塔方式組織變換系數(shù)，再通過圖的形式從金字塔中提取小線變換系數(shù)，從而實(shí)現(xiàn)多尺度分析。這是一種能較好進(jìn)行二維或更高維奇異性分析的工具。

　　根據(jù)小線理論及其研究結(jié)果來看，它對(duì)于處理強(qiáng)噪背景的圖像有無可比擬的優(yōu)勢(shì)。但是小線變換的前期準(zhǔn)備工作，如小線字典、小線金字塔掃描這些部分的工作量太過于龐大，不利于研究。如果能將這部分簡(jiǎn)化，或者做成固定的模塊引用的話，相信小線分析能夠很快的擴(kuò)展其應(yīng)用領(lǐng)域。總的來說小線分析的研究還處于初步階段，相關(guān)的研究成果也不多，應(yīng)用研究領(lǐng)域有待于進(jìn)一步拓展。

　　在Beamlet分析中，線段類似于點(diǎn)在小波分析中的地位。Beamlet 能夠提供基于二進(jìn)組織的線段的局部尺度、位置和方向表示，線的精確定位易實(shí)現(xiàn)，且算法實(shí)現(xiàn)不復(fù)雜，所以基于Beamlet 的線特征提取值得研究。

　　Beamlet基是一個(gè)具有二進(jìn)特征的多尺度的有方向的線段集合，二進(jìn)特征體現(xiàn)在線段的始終點(diǎn)坐標(biāo)是二進(jìn)的，尺度也是二進(jìn)的。

　　Donoho 提出了連續(xù)Beamlet變換及其在多尺度分析中的應(yīng)用，為減少計(jì)算量及更適于計(jì)算機(jī)處理，Xiaoming Huo 提出了離散Beamlet變換。

　　從Beamlet基的框架得知，每條Beamlet把每個(gè)二進(jìn)方塊分為兩個(gè)部分，每個(gè)部分都稱為Wedgelet，這兩部分為互補(bǔ)的Wedgelet，從而每個(gè)Beamlet對(duì)應(yīng)兩個(gè)互補(bǔ)的Wedgelet，使Beamlet基與Wedgelet對(duì)應(yīng)起來Wedgelet變換具有多尺度的特性；還可以看出Wedgelet基是片狀基，與Beamlet的線狀基不同。