????? 在SoC(System on Chip)廣泛應(yīng)用的今天，如何設(shè)計(jì)一個基于Ic的RiNG就成為安全通信應(yīng)用的急切需要。隨機(jī)噪聲源(如熱噪聲和發(fā)射噪聲)存在于IC中卻總是被人為地屏蔽掉了。因此，利用電路噪聲放大的商用RNG設(shè)計(jì)需要專門的外部組件和特殊硬件來與那些需要屏蔽噪聲的組件隔開。在IC設(shè)計(jì)中，對數(shù)模混合信號的處理經(jīng)驗(yàn)表明，底層噪聲和電源噪聲電平總是高于隨機(jī)噪聲源電平。所以一個不被干擾的白噪聲源在一個基于IC的數(shù)字加解密系統(tǒng)的RNG中是不可能被使用的，必須考慮如何利用抗干擾的隨機(jī)源來實(shí)現(xiàn)隨機(jī)數(shù)生成器。 　　
本文提出一種新的混沌RNG的實(shí)現(xiàn)方案，更易于用硬件即IC實(shí)現(xiàn)。首先討論其原理和模型及其實(shí)驗(yàn)，并對其進(jìn)行隨機(jī)性測試；然后討論它的FPGA實(shí)現(xiàn)方案。
　　
1 模型及實(shí)驗(yàn)
　　
1．1 隨機(jī)數(shù)生成器的定義
　　
定義1 一個理想的隨機(jī)數(shù)生成器是一個生成等概率符號的離散無記憶信息源(DMIS)，RNG是一個有著正熵的離散信息源。


　　
但是，現(xiàn)實(shí)中的RNG都是產(chǎn)生非均勻概率符號的離散有記憶信息源。因此采用有偏差的RNG來區(qū)別于定義1中理想的RNG。一個有偏差的RNG性能的好壞可通過它的冗余度ρ=log2Q-h來衡量，其中Q和h分別是離散符號集的基數(shù)和相關(guān)信源的熵。一個理想RNG的冗余度應(yīng)該等于O，而一個有偏差的RNG的冗余度則標(biāo)志這個RNG跟理想RNG的差距。例如一個冗余度為ρ的RNG產(chǎn)生長度為N位的密鑰，則攻擊方平均要嘗試2(1-ρ)N個密鑰才能找到正確的密鑰，因此密鑰的有效長度可以被定義為Ne=(1-ρ)N。
　　
1．2 混沌隨機(jī)數(shù)生成器模型
　　
混沌理論作為非線性動態(tài)系統(tǒng)的分支，近年來受到越來越多的關(guān)注。它使得一個低維動態(tài)系統(tǒng)也可以擁有復(fù)雜的、不可預(yù)料的行為，使復(fù)雜的方程不再是生成隨機(jī)數(shù)序列的必要條件。
　　
混沌系統(tǒng)可以用基于下列迭代關(guān)系式描述的Bemouli移位映射：

　　
式中，e(n)表示一個高斯噪聲信號。這個迭代式表明由(1)式產(chǎn)生的序列是極為平滑和均一分布的。另外，與混沌相關(guān)的軌跡發(fā)散包含了噪聲,(1)式產(chǎn)生的序列在一定范圍內(nèi)是不可預(yù)測的，從而使系統(tǒng)能被當(dāng)作一個真隨機(jī)比特源。離散時間混沌法不受其他噪聲源影響。
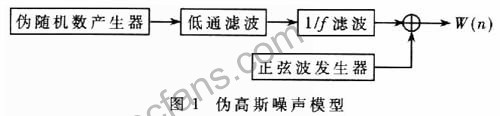
　　在電路上實(shí)現(xiàn)Bemouli移位映射的關(guān)鍵在于實(shí)現(xiàn)一個抗干擾的高斯噪聲信號。傳統(tǒng)的混沌隨機(jī)數(shù)生成器是用一個偽隨機(jī)數(shù)生成器產(chǎn)生一個偽高斯噪聲信號來實(shí)現(xiàn)(1)中的e(n)，如圖1所示，這在一定程度上降低了混沌隨機(jī)數(shù)生成器的安全性和真隨機(jī)性。

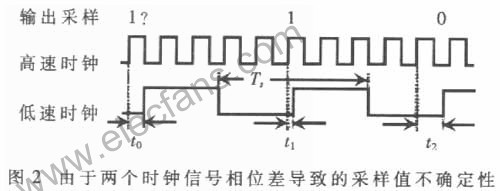
典型的振蕩器采樣法是利用時鐘的相位噪聲(理論上是MOSFET熱噪聲的副產(chǎn)品)產(chǎn)生隨機(jī)數(shù)。通過一個由較慢時鐘信號控制的D觸發(fā)器對一個高速時鐘進(jìn)行采樣，高速時鐘的相位抖動導(dǎo)致具體采樣值的不確定性，如圖2所示，理論上每次采樣都會產(chǎn)生一個隨機(jī)比特。典型采樣后的抖動電平是符合高斯分布的，而且這種抖動不會受到電路中其他噪聲的干擾。另外，振蕩器采樣法的隨機(jī)性可以通過仔細(xì)挑選快的和慢的時鐘頻率比來人為增強(qiáng)。采樣時發(fā)生的非線性偏移現(xiàn)象使得這種振蕩器采樣技術(shù)比目前的確定性噪聲更健壯。

　　
基于上述原理，提出用振蕩器采樣輸出作為一個高斯噪聲信號e(n)實(shí)現(xiàn)(1)式。結(jié)合兩種隨機(jī)數(shù)生成器方案實(shí)現(xiàn)混沌隨機(jī)數(shù)生成器，系統(tǒng)原理框圖如圖3所示。

　　
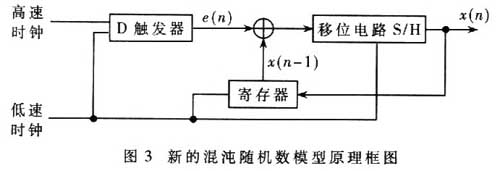
其中S／H(Shilt／Hold)為一個移位保持電路，用來實(shí)現(xiàn)2(x(n-1)+e(n))。低速時鐘控制D觸發(fā)器、寄存器和S／H。寄存器中殘余信號作為初始輸人信號，然后與振蕩1．3 實(shí)驗(yàn)結(jié)果及討論
　　
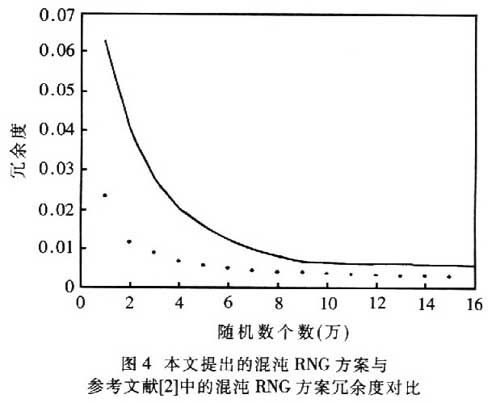
根據(jù)前面的定義l來檢測本文中提出的混沌RNG的性能，用它生成不同長度的8bit隨機(jī)數(shù)序列，計(jì)算其冗余度，并與參考文獻(xiàn)中的傳統(tǒng)混沌RNG方案做對比，如圖4所示，點(diǎn)線表示本文提出的方案，實(shí)線表示69是文獻(xiàn)中的方案。通過對比可以很明顯地看出改進(jìn)后的混沌RNC性能優(yōu)于采用偽隨機(jī)高斯噪聲的傳統(tǒng)混沌RNG方案。

　　
僅僅由冗余度來衡量一個RNG是不夠的。為了了解本文提出的混沌RNG輸出序列的隨機(jī)性是否實(shí)現(xiàn)了“隨機(jī)”，我們根據(jù)美國國家標(biāo)準(zhǔn)及技術(shù)研究所(NIST)的要求對本文的混沌RNC方案產(chǎn)生的隨機(jī)數(shù)序列的隨機(jī)性進(jìn)行一系列測試。測試所用數(shù)據(jù)為慢速時鐘=8kHz，高速時鐘=100MHz，輸出精度為8bit的輸出值，測試長度為3 000 000個8位隨機(jī)數(shù)的序列，表1為測試結(jié)果。

　　
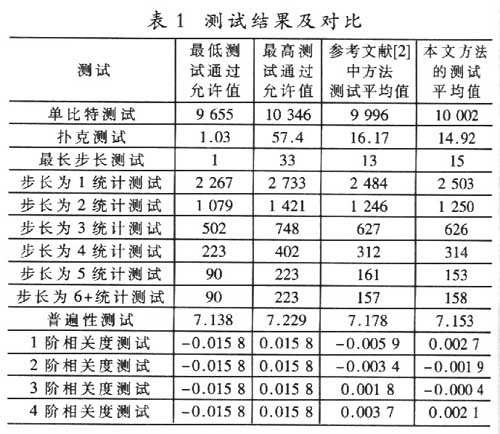
經(jīng)過以上一系列的隨機(jī)性測試，RNG表現(xiàn)良好，在置信水平為95％的情況下通過了全部測試，沒有表現(xiàn)出非隨機(jī)性，并且在信源相關(guān)度的測試(correlation order test)中性能超過了參考文獻(xiàn)中的混沌RNG方案。這項(xiàng)測試是測試一個隨機(jī)數(shù)序列的相鄰隨機(jī)數(shù)的相關(guān)度。一個理想RNG的前后隨機(jī)數(shù)相關(guān)度應(yīng)該為0。由表1中數(shù)據(jù)可知，本文的混沌RNG測試結(jié)果更接近于理想RNG。因此可以認(rèn)為，就目前已知的測試隨機(jī)數(shù)的隨機(jī)性的測試結(jié)果表明，本文介紹的混沌RNG生成的隨機(jī)數(shù)序列是比較好的。
　　
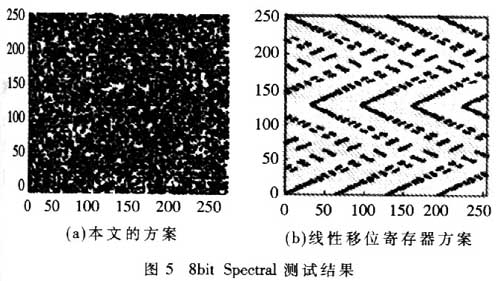
光譜測試可以直觀地顯示出隨機(jī)數(shù)序列與其自身的相關(guān)情況。通過圖5可以更直觀地看到一個相關(guān)度低的RNG與一個偽RNG(用10位線性反饋移位寄存器來做例子)的對比。相關(guān)度為0的理想RNG應(yīng)該均勻分布在整個二維空間內(nèi)，線性反饋移位寄存器的測試結(jié)果(圖b)就反映出了它的高相關(guān)度，而本文提出的混沌RNG方案的測試結(jié)果(圖a)則顯示了其不可預(yù)測性與無規(guī)則性分布。

　　
2 硬件實(shí)現(xiàn)
　　
本文采用Xilinx公司的xuPV2P30開發(fā)板實(shí)現(xiàn)這個混沌KNG，這塊開發(fā)板上自帶兩個獨(dú)立的(不同相位)時鐘源，二者都可以輸出8k～100MHz的不同頻率的時鐘。選擇慢速時鐘信號頻率范圍為8k～1MHz，高速時鐘信號頻率為100MHz，輸出精度為8bit。其邏輯使用資源情況如表2所示。

　　
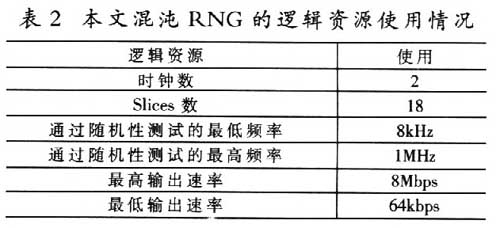
從表2可以看到，在硬件上以極低的邏輯資源使用(18個Slices約合1800+門)實(shí)現(xiàn)了本文提出的混沌RNG方案，對比參 考文獻(xiàn)中的方案(3000+門)，該電路得到大大簡化，而參考文獻(xiàn)中的偽高斯噪聲生成器占用了很大的硬件資源。該方案的最高輸出速率受到了板載最高時鐘頻率的限制。如果本文的混沌RNG用IC方案實(shí)現(xiàn)，則可以進(jìn)一步減小所需要的硬件資源并進(jìn)一步提高輸出速率。
　　
本文提出的方案通過了一系列高要求的隨機(jī)性測試，其邏輯資源的占用遠(yuǎn)小于傳統(tǒng)的混沌RNG方案，最高輸出速率可達(dá)8Mbps。因而這種RNG方案可以用于對安全性和性能需求日益增長的加密系統(tǒng)中。

生成器采樣輸出信號進(jìn)行模2加操作(異或)，再通過S／H產(chǎn)生最后的輸出x(n)，x(n)被反饋到寄存器中進(jìn)行下次操作。