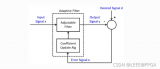
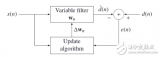
自適應濾波器是指根據環境的改變，使用自適應算法來改變濾波器的參數和結構的濾波器。一般情況下，不改變自適應濾波器的結構。而自適應濾波器的系數是由自適應算法更新的時變系數。即其系數自動連續地適應于給定信號，以獲得期望響應。自適應濾波器的最重要的特征就在于它能夠在未知環境中有效工作，并能夠跟蹤輸入信號的時變特征。

　　自適應濾波器的作用

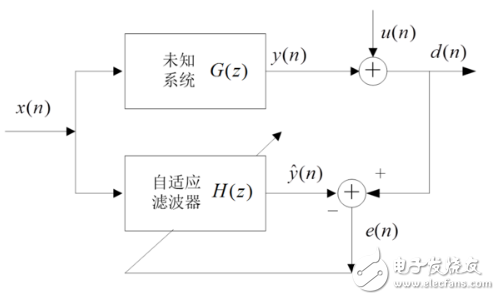
　　1、系統辨識：這時參考信號就是未知系統的輸出，當誤差最小時，此時自適應濾波器就與未知系統具有相近的特性，自適應濾波器用來提供一個在某種意義上能夠最好擬合未知裝置的線性模型。當我們想描述一個未知系統（如一組復雜的模擬電路），解析的算出系統的沖擊響應或者系統函數是比較困難的。這時，我們就可以用未知系統的輸入和輸出訓練自適應濾波器（未知系統的輸入作為自適應濾波器的輸入，未知系統的輸出作為自適應濾波器的期望信號，當自適應濾波器收斂后，對應的濾波器就可以看做是未知系統的近似）。

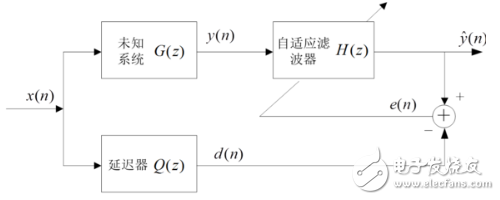
　　2、逆系統辨識：在這類應用中，自適應濾波器的作用是提供一個逆模型，該模型可在某種意義上最好擬合未知噪聲裝置。理想地，在線性系統的情況下，該逆模型具有等于未知裝置轉移函數倒數的轉移函數，使得二者的組合構成一個理想的傳輸媒介。該系統輸入的延遲構成自適應濾波器的期望響應。在某些應用中，該系統輸入不加延遲地用做期望響應。

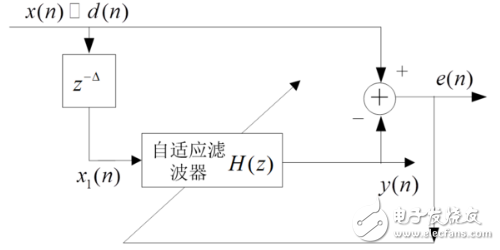
　　3、預測：在這類應用中，自適應濾波器的作用是對隨機信號的當前值提供某種意義上的一個最好預測。于是，信號的當前值用作自適應濾波器的期望響應。信號的過去值加到濾波器的輸入端。取決于感興趣的應用，自適應濾波器的輸出或估計誤差均可作為系統的輸出。在第一種情況下，系統作為一個預測器；而在后一種情況下，系統作為預測誤差濾波器。

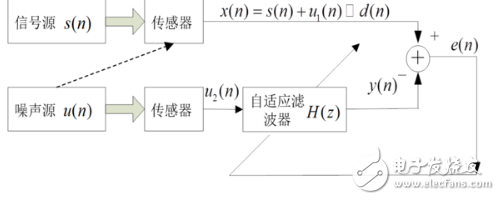
　　4、干擾消除：在一類應用中，自適應濾波器以某種意義上的最優化方式消除包含在基本信號中的未知干擾。基本信號用作自適應濾波器的期望響應，參考信號用作濾波器的輸入。參考信號來自定位的某一傳感器或一組傳感器，并以承載新息的信號是微弱的或基本不可預測的方式，供給基本信號上。這種類型自適應濾波器的輸入信號為噪聲源，期望信號信號為含有噪聲的信號源。經過多次迭代后，期望信號和自適應濾波器的輸出信號之差就是信號源的估計。

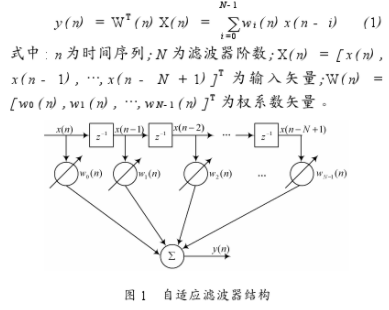
　　自適應濾波器的原理

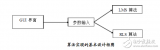
　　1、最小均方（LMS）誤差算法：

　　最簡單的LMS算法是通過每一次迭代輸入的數據對當前的目標函數的梯度進行估計，從而得到相應輸入信號的自相關矩陣R與互相關向量p。則得到的梯度估計值為：

　　gw（k）=-2p（k）+2R（k）w（k）=2x（k）（-d（k）+w（k）（k））=-2e（k）x（k）

　　則濾波系數更新方程為：w（k+1）=w（k）+2niu*e（k）x（k）

　　整理可得LMS算法：

　　初始化部分：

　　w（k）=［00…0］T

　　單次迭代部分：

　　e（k）=d（k）-w（k）（k）

　　w（k+1）=w（k）+2niu*e（k）x（k）

　　其中niu參數表示單次調節的步長，是一個常數需要在實際的應用中進行確定。我們可以得到單次迭代所需要進行的乘法次數為O［N］量級，N表示FIR濾波器的系數矢量w（k）的維數，該算法已經具有一定的實際應用的價值，如果對濾波的精度要求不是很高，而且對每次迭代速度有很高的要求的話，此算法非常合適。

　　2、遞歸最小二乘（RLS）算法：

　　在上一節中我們知道，基于瞬時梯度估計的LMS算法實際上只使用了當前時刻的輸入信號矢量x（k）和期望信號d（k），沒有利用過去的信息這就導致梯度估計的誤差很大算法收斂的數度慢，一個很直接的想法就是如果能把過去的信息利用起來，那么梯度估計的誤差就會大大的減小，算法很快就會收斂。最小二乘（RL）算法正好就實現了這一過程，它旨在使期望信號與模型濾波器輸出之差的平方和最小。具體的算法推導比較的復雜，這里不方便編輯公式同時也沒有必要，在這里給出了其算法實現語言描述部分。

　　下面對其中的一些相關變量名做一下解釋，SD（k）表示輸入信號矢量的確定性自相關矩陣（RD（k））的逆，e（k）表示先驗誤差，epsilon（k）表示后驗誤差（就是圖片中的希臘字母epsilon，由于不方便輸入所以用它代替了，后面還有一個哦），lambda表示遺忘因子，意思就是隨著時間的推移以前的“舊”的信號對濾波器系數調整的影響越小，主要由更新的數據決定，從這個角度說明了該算法對非平穩的信號也能進行自適應濾波。其它的變量同上。從上面的描述可以看出單次迭代運算量在O［N2］量級，比LMS的計算量要大。

　　自適應濾波器的應用

　　自適應濾波處理技術可以用來檢測平穩的和非平穩的隨機信號。自適應數字系統具有很強的自學習、自跟蹤能力和算法的簡單易實現性。它是從六十年代初發展起來的，與信息論、檢測及最佳估計理論、濾波器理論密切相關，是信號處理學科的一個重要分支，隨著超大規模集成電路技術和計算機技術的迅速發展和自適應濾波理論本身的不斷完善，使得其應用愈末愈廣泛，已遍及通信、語音信號處理、圖像處理、模式識別、系統辨識及自動控制等領域，是目前最活躍的研究領域之一。自適應濾波器的應用范圍很廣，主要有五個方面：自適應濾波與逆濾波；系統辨識；自適應均衡：自適應回波抵消；通信中的噪聲消除。

　　1、自適應濾波與逆濾波

　　對一個未知系統的逆系統進行模擬叫做系統的逆向模擬，可以看成求一自適應系統，其傳函數是未知系統的傳遞函數的倒數的最佳擬合，或者說求一未知系統的逆濾波系統。自適應逆濾波應用廣泛，它可以作為信道均橫器，在數字數據傳輸中，信道常等效成一個線性時不變系統，為了抵消信道失真，常在接收端用一個自適應逆濾波器進行處理，其傳遞函數等于信道傳遞函數的倒數。

　　2 、系統辨識

　　所謂系統辨識，實質上是根據系統的輸入和輸出信號來估計或確定系統的特性以及系統的單位脈沖響應或傳遞函數。系統辨識的任務是根據輸入信號和接收信號確定未知信道的特性。用自適應濾波器模擬未知系統，并通過調整其參數，使它在與未知系統具有相同激勵時能夠得到誤差均方值最小的輸出。自適應濾波器收斂后，其結構和參數不一定會與未知系統的結構和參數相同，但二者的輸入，輸出響應關系是擬合的或匹配的。

　　3、自適應均衡

　　計算機通信的快速發展，要求提高數據傳輸系統的速率。在有限傳輸系統中，當數據速率高于4800b礁時，由于有線信道的傳輸特性不理想，而且其幅度響應與相頻響應分別是恒定的和線性的，會隨著氣候、氣溫等因素而變化，因此必須采用自適應均衡器來補償信道的畸變，以減少碼間干擾所引起的誤碼。在數字微波接力通信系統中，由于多徑傳輸所引起的碼問干擾，也必須采用自適應均衡器來克服它。

　　4、自適應回波抵消

　　所謂回波，一般指信號源發生的、經過信道或目標而返回到信號源的一部分原始信號。這種返回的信號相對于信號源發出的原始信號，往往有一定的延遲或失真。在諸如雷達、主動聲納和超聲檢測等應用中，回波就是所要接收或檢測的信號，其中包含了目標或信號傳輸通道的相關信息。然而，在通信系統中，回波與噪聲一樣，都會對通信質量產生有害的影響，必須加以消除。通常，通信系統中存在兩種類型的回波，即電回波和聲回波。電回波又稱線路回波，是通信信號在傳輸媒介中傳輸時，由于阻抗的不匹配引起的。而聲回波是由聲波的反射及麥克風和揚聲器之間的聲音耦合造成的。回波對通信用戶而言是非常有害的，同時也會影響信號檢測的準確性和可靠性。例如，在語音識別應用中，原始語音信號的回波可能會被誤認為是原始語音信號。這樣，語音識別系統的有效性會因回波的影響而大打折扣。類似地，在多方電話會議應用中，由于信號經過多次阻抗不匹配情況下的反復傳播，影響會更加嚴重。為了克服影響，可在終端裝上自適應回波抵消器。

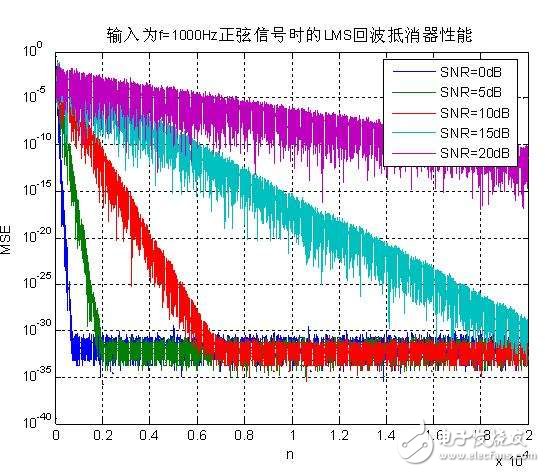
　　5、通信中的噪聲消除

　　噪聲消除是信號處理的核心問題之一，也是通信系統面臨的關鍵問題。傳統的濾波技術是一種常規的噪聲消除技術，包括維納濾波和卡爾曼濾波在內，傳統的濾波技術均要求已知信號和噪聲的統計先驗知識。但是在許多實際應用中，這些統計特性往往無法預先得知。1959年，美國斯坦福大學建成了第一個自適應噪聲抵消系統（Adaptive Noise Cancellation，ANC），四十多年來，自適應噪聲抵消系統在許多領域得到了廣泛的應用。

　　總結

　　鑒于自適應濾波器具有自學習、自跟蹤、對參數經常變化的動態系統有較好控制效果的特性，我們有必要對其進行深入的研究，特別是對自適應濾波器新算法的研究。