帶通濾波器電路圖設計(一)
傳統的帶通濾波器設計方法中涉及了很多復雜的理論分析和計算。針對上述缺點,介紹一種使用EDA軟件進行帶通濾波器的設計方案,詳細闡述了使用FilterPro軟件進行有源帶通濾波器電路的設計步驟,然后給出了在Proteus中對所設計的濾波器進行仿真分析和測試的方法。測試結果表明,使用該方法設計的帶通濾波器具有性能穩定。設計難度小等優點,也為濾波器的設計提供了一個新的思路。
帶通濾波器是一種僅允許特定頻率通過,同時對其余頻率的信號進行有效抑制的電路。由于它對信號具有選擇性,故而被廣泛地應用現在電子設計中。但是,帶通濾波器的種類繁多,各個類型的設計差異也很大,這就導致了在傳統濾波器的設計方法中不可避免地要進行大量的理論計算與分析,不但損失了寶貴的時間,同時也提升了電路的設計門檻。為了解決上述弊端,本文介紹了一種使用FilterPro和Proteus相結合的有源帶通濾波器的設計方案,隨著EDA技術的不斷發展,這種方法的優勢也將越來越明顯。
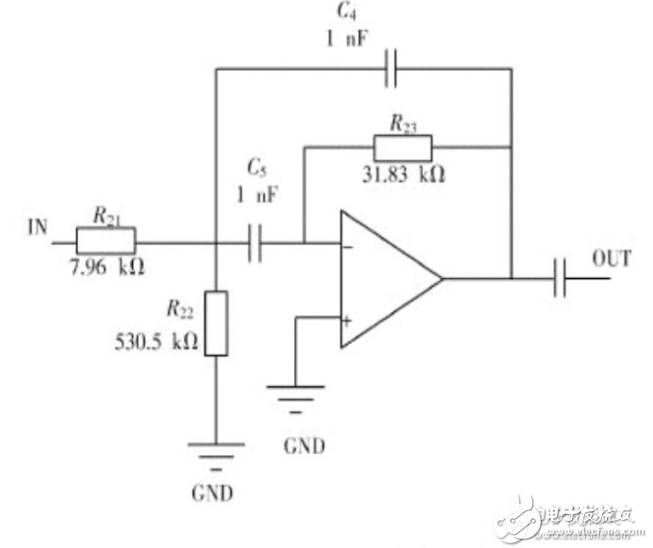
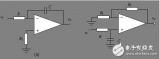
圖1 ?使用理想運放的帶通濾波器
電路原理圖如圖1所示。然后可在Proteus中搭建電路進行仿真分析,前面已經提到,FilterPro生成的濾波器中的運放使用的理想運放模型,所以仿真時需要先用理想運放進行分析,然后再進行替換。
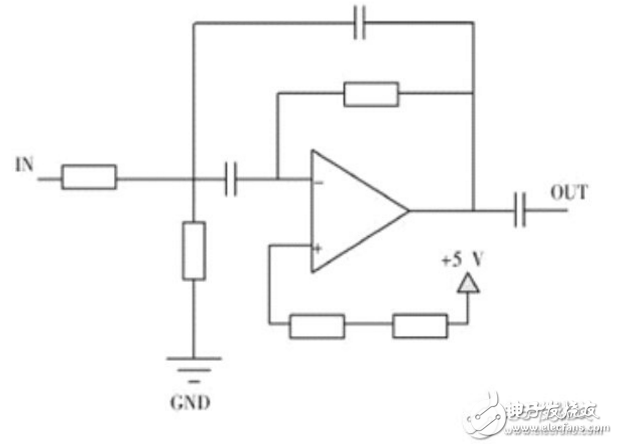
圖2 ?實際搭建的濾波器電路
設計中運放選擇TI產品典型的通用雙放LM358,LM358里面包括兩個高增益、獨立的、內部頻率補償的雙運放,適用于電壓范圍很寬的單電源,而且也適用于雙電源工作方式,特點方面具有低輸入偏置電流、低輸入失調電壓和失調電流,它的共模輸入電壓范圍較寬,差模輸入電壓范圍等于電源電壓范圍,單電源供電電壓3-32V,雙電源供電±1.5-±16V,單位增益帶寬為1MHz,適用于一般的帶通濾波器的設計,同時具有低功耗的功能,對于設計階數相對高一些的帶通濾波器的話,可以選用TI的四運放LM324,其性能與LM358大體相同,應用起來節省空間。對于運放的要求此設計不是特別高,只要運放的頻率滿足低通的截止頻率即可,如果精確度要求高的話那么首先運放的供電電壓要足夠穩定,或者選擇精密運放,如TLC274A,否則通用的即可,例如推薦TI的LM224四運放。
巴特沃斯帶通濾波器幅頻響應在通帶中具有最平幅度特性,但是從通帶到阻帶衰減較慢,如果對于過渡帶要求稍高,可以增加階數來實現,否則改選用切比雪夫濾波電路。
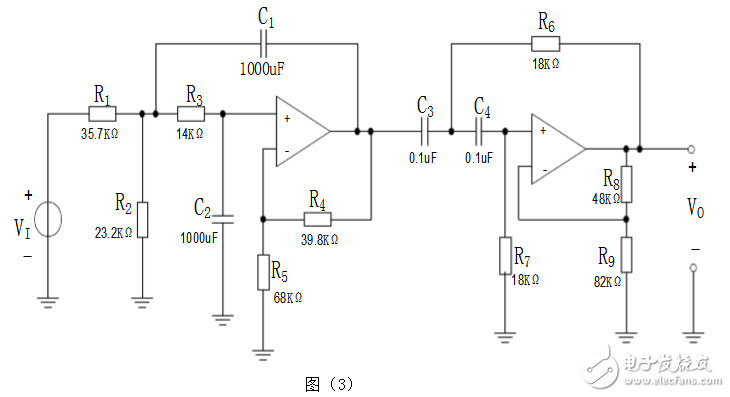
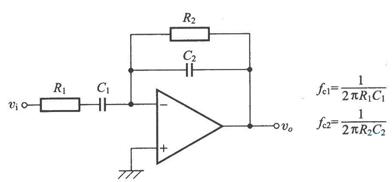
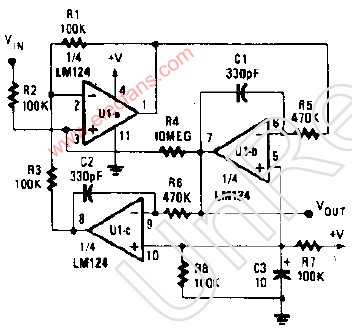
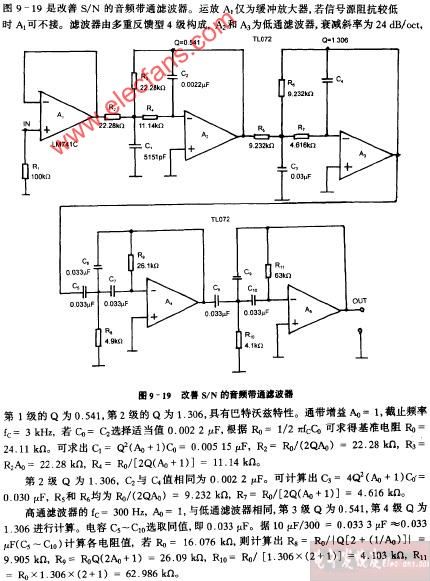
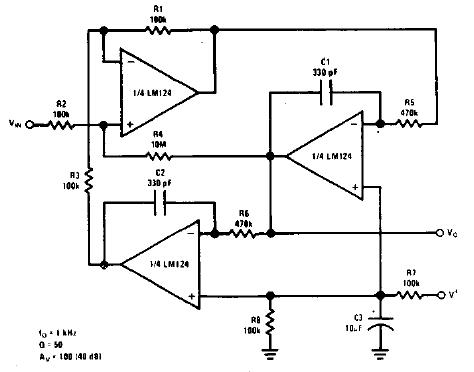
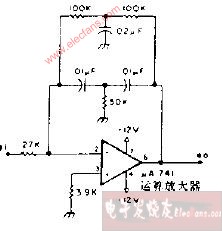
下面討論設計兩種帶通濾波器,其一為二階低通濾波器和二階高通濾波器組成的四階帶通濾波器,如下圖:
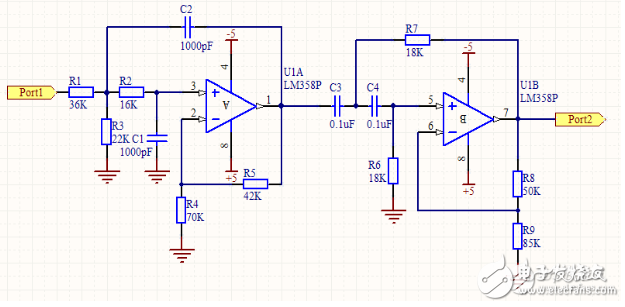
圖 3 ?四階帶通濾波器
參數選擇與計算:
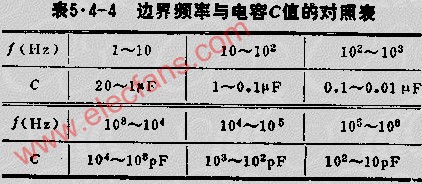
對于低通濾波器的設計,電容一般選取1000pF,對于高通濾波器的設計,電容一般選取0.1uF,然后根據公式R=1/2Πfc計算得出與電容相組合的電阻值,即得到此圖中R2、R6和R7,為了消除運放的失調電流造成的誤差,盡量是運放同相輸入端與反向輸入端對地的直流電阻基本相等,同時巴特沃斯濾波器階數與增益有一定的關系(見表1),根據這兩個條件可以列出兩個等式:30=R4*R5/(R4+R5),R5=R4(A-1),36=R8*R9/(R8+R9),R8=R9(A-1)由此可以解出R4、R5、R8、R9,原則是根據現實情況稍調整電阻值保持在一定限度內即可,不要相差太大,注意頻率不要超過運放的標定頻率。
表1巴特沃斯低通、高通電路階數與增益的關系
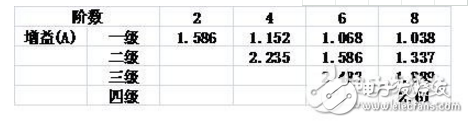
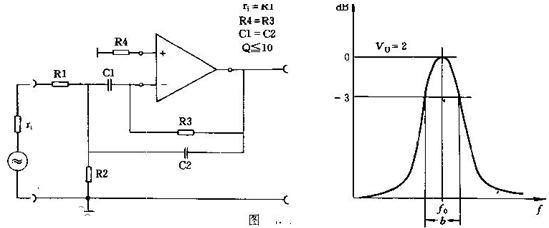
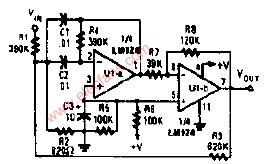
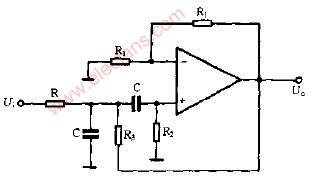
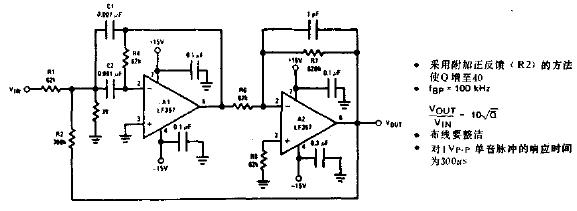
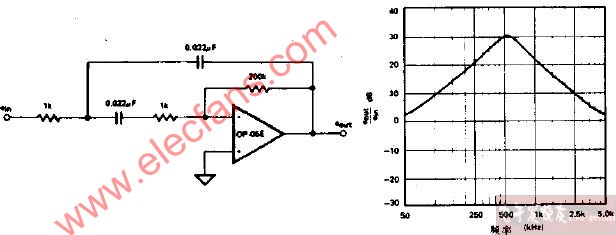
其二是二階有源帶通濾波器,只用一個放大區間,如下圖:
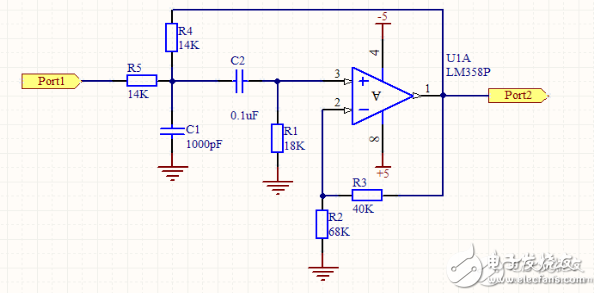
圖4 ?二階帶通濾波器
帶通濾波器電路圖設計(二)
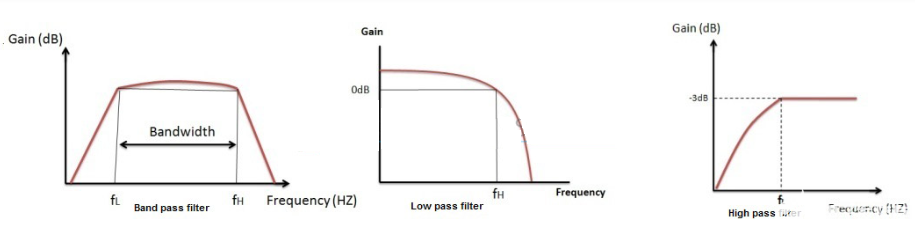
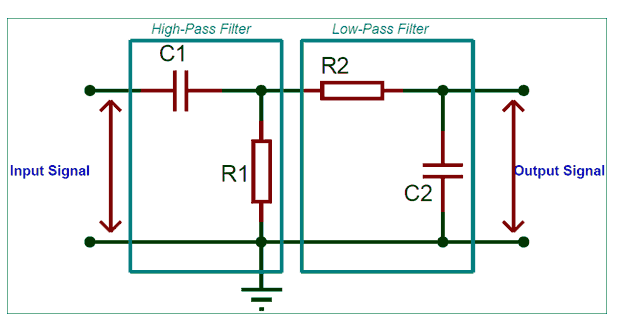
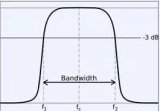
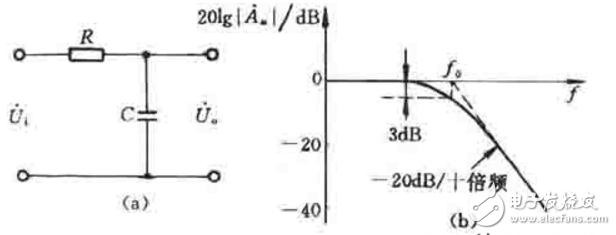
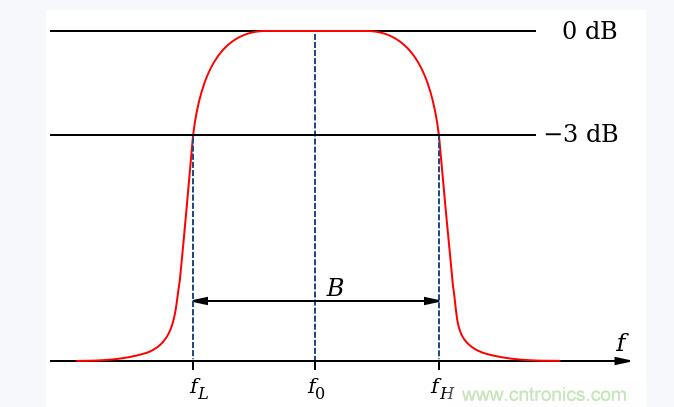
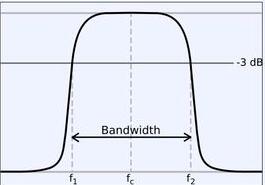
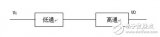
由圖(1)所示帶通濾波電路的幅頻響應與高通、低通濾波電路的幅頻響應進行比較,不難發現低通與高通濾波電路相串聯如圖(2),可以構成帶通濾波電路,條件是低通濾波電路的截止角頻率WH大于高通電路的截止角頻率WL,兩者覆蓋的通帶就提供了一個帶通響應。
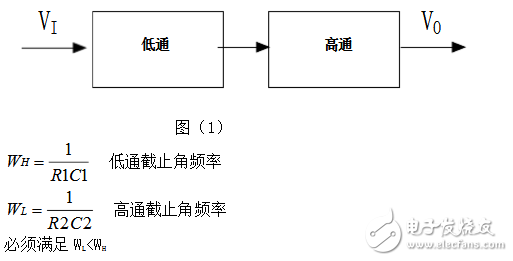
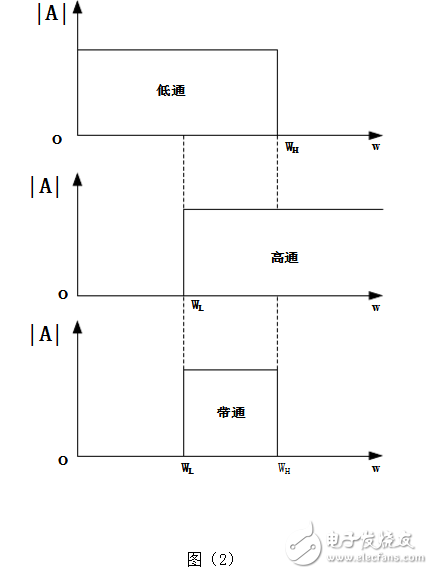
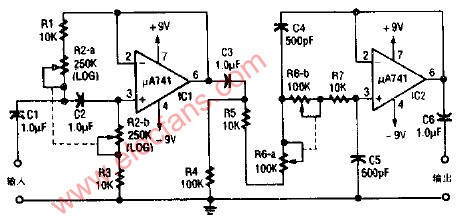
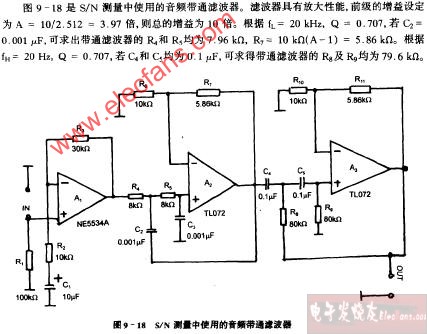
這是一個通帶頻率范圍為100HZ-10KHZ的帶通濾波電路,在通帶內我們設計為單位增益。根據題意,在頻率低端f=10HZ時,幅頻響應至少衰減26dB。在頻率高端f=100KHZ時,幅頻響應要求衰減不小于16dB。因此可以選擇一個二階高通濾波電路的截止頻率fH=10KHZ,一個二階低通濾波電路的fL=100HZ,有源器件仍選擇運放LF142,將這兩個濾波電路串聯如圖所示,就構成了所要求的帶通濾波電路。
由巴特沃斯低通、高通電路階數n與增益的關系知Avf1=1.586,因此,由兩級串聯的帶通濾波電路的通帶電壓增益(Avf1)2=(1.586)2=2.515,由于所需要的通帶增益為0dB,因此在低通濾波器輸入部分加了一個由電阻R1、R2組成的分壓器。
元件參數的選擇和計算
在選用元件時,應當考慮元件參數誤差對傳遞函數帶來的影響。現規定選擇電阻值的容差為1%,電容值的容差為5%。由于每一電路包含若干電阻器和兩個電容器,預計實際截止頻率可能存在較大的誤差(也許是+10%)。為確保在100Hz和10kHz處的衰減不大于3dB.現以額定截止頻率90Hz和1kHz進行設計。
前已指出,在運放電路中的電阻不宜選擇過大或較小。一般為幾千歐至幾十千歐較合適。因此,選擇低通級電路的電容值為1000pF,高通級電路的電容值為0.1μF,然后由式RCWC1?可計算出精確的電阻值。
對于低通級由于已知c=1000pF和fh=11kHz,由式RCWC1?算得R3=14.47kΩ,先選擇標準電阻值R3=14.0kΩ。對于高通級可做同樣的計算。由于已知C=0.1μF和fL=90Hz,可求出R7=R8≈18kΩ。
考慮到已知Avf1=1.586,同時盡量要使運放同相輸入端和反相輸入端對地的直流電阻基本相等,現選擇R5=68k,R10=82k,由此可算出R4=(Avf1-1)R5≈39.8k,R9=(Avf1-1)R10≈48k,其容差為1%。
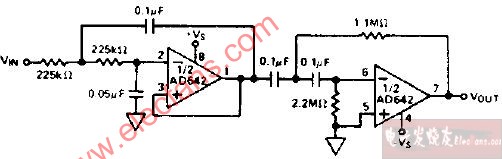
設計完成的電路如圖所示。信號源vI通過R1和R2進行衰減,它的戴維寧電阻是R1和R2的并聯值,這個電阻應當等于低通級電阻R3(=14k)。因此,有????
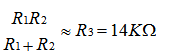
由于整個濾波電路通帶增益是電壓分壓器比值和濾波器部分增益的乘積,且應等于單位增益,
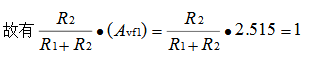
聯解式和,并選擇容差為1%的額定電阻值,得R1=35.7kΩ和R2=23.2kΩ。
帶通濾波器電路圖設計(三)
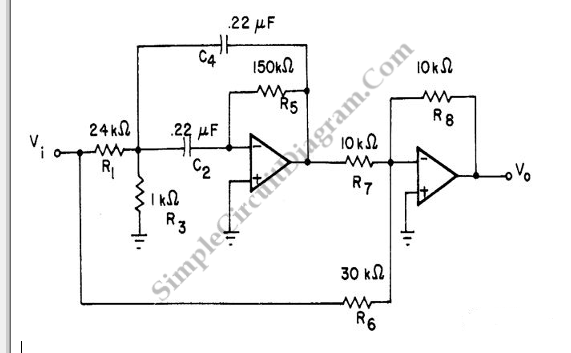
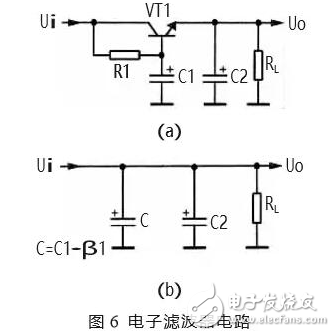
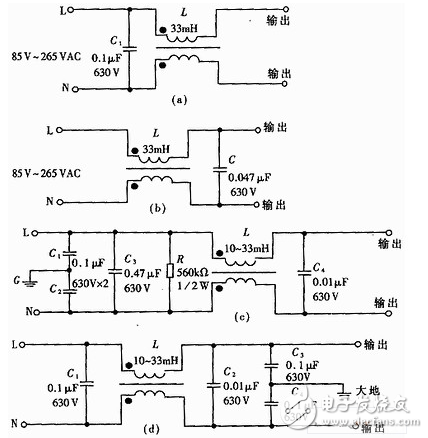
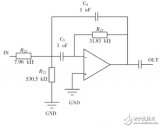
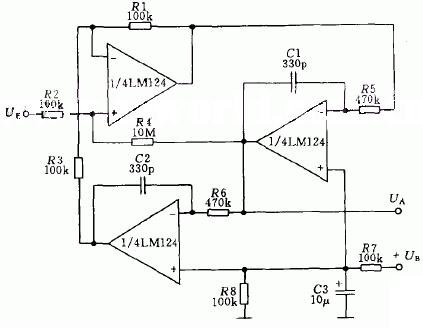
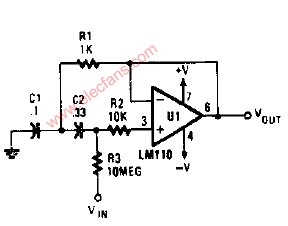
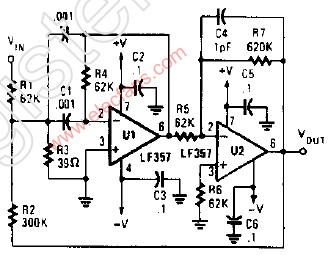
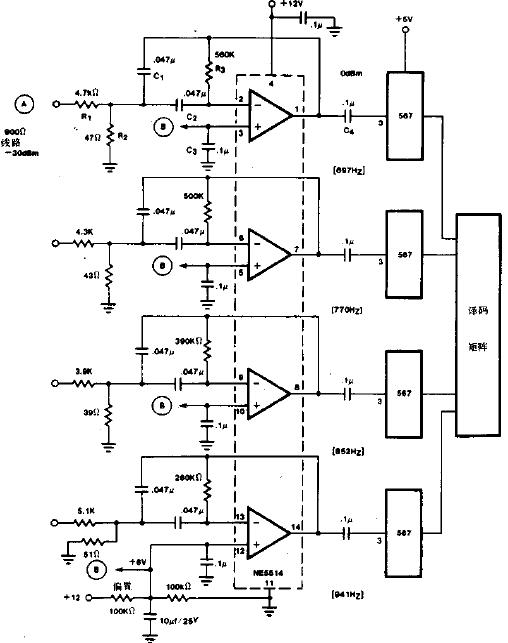
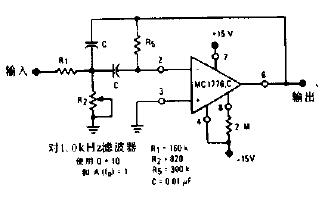
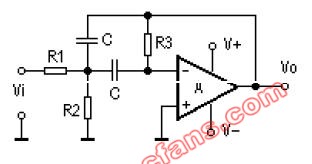
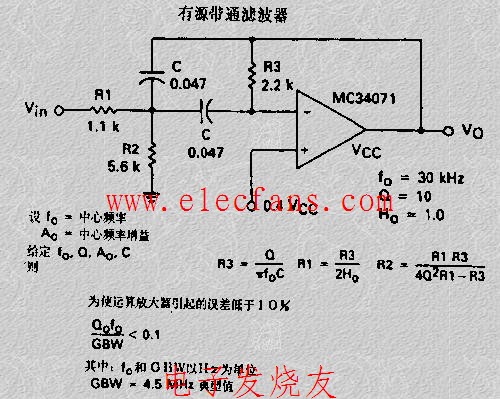
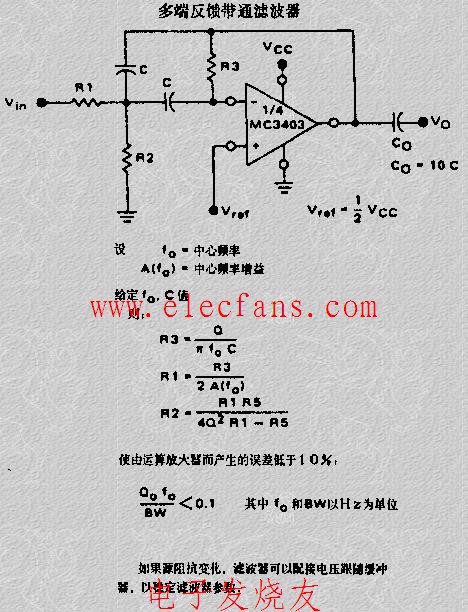
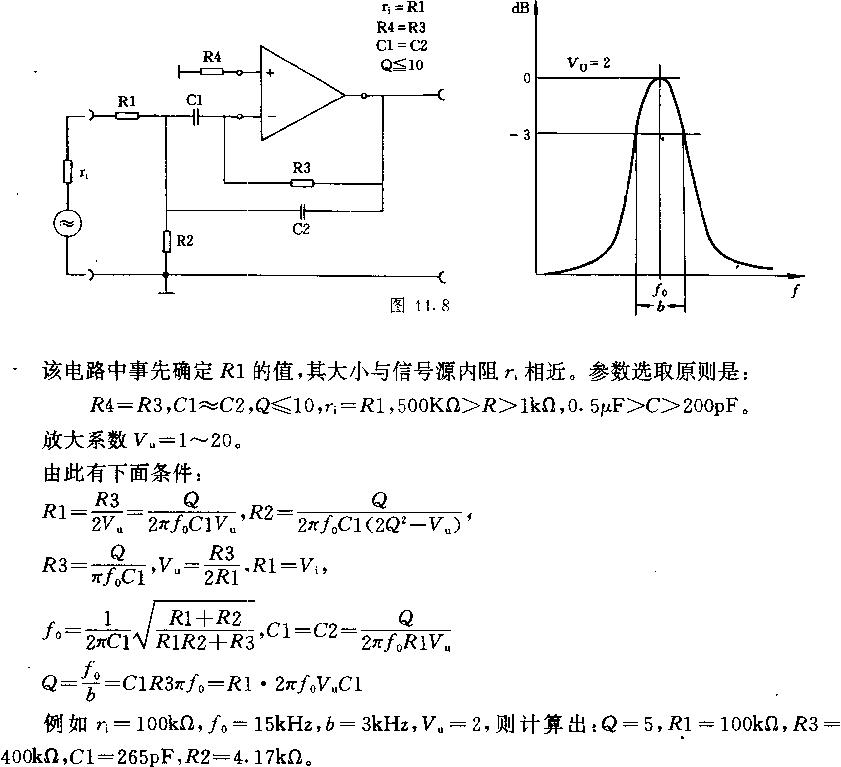
實用的帶通濾波器電路原理圖

該電路在負反饋支路上是一個帶阻濾波齊器,以使其只允許通過被反饋支路阻斷的頻率信號。

 電子發燒友App
電子發燒友App










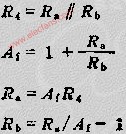
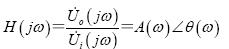














評論