1 前言
由于后續(xù)更新「面試專(zhuān)場(chǎng)」的好幾篇文章都涉及到圖這種數(shù)據(jù)結(jié)構(gòu),因此打算先普及一下 圖 的相關(guān)理論支持,如果后面的相關(guān)內(nèi)容有些點(diǎn)不太容易理解,可以查閱此篇文章。本文不建議一口氣閱讀完畢,可以先瀏覽一遍,在后續(xù)有需要的時(shí)候進(jìn)行查閱即可。
2 圖
圖是數(shù)據(jù)結(jié)構(gòu)中重要內(nèi)容。相比于線(xiàn)性表與樹(shù),圖的結(jié)構(gòu)更為復(fù)雜。在線(xiàn)性表的存儲(chǔ)結(jié)構(gòu)中,數(shù)據(jù)直接按照前驅(qū)后繼的線(xiàn)性組織形式排列。在樹(shù)的結(jié)構(gòu)中,數(shù)據(jù)節(jié)點(diǎn)以層的方式排列,節(jié)點(diǎn)與節(jié)點(diǎn)之間是一種層次關(guān)系。但是,在圖的結(jié)構(gòu)中數(shù)據(jù)之間可以有任意關(guān)系,這就使得圖的數(shù)據(jù)結(jié)構(gòu)相對(duì)復(fù)雜。
2.1 定義
定義:圖(Graph)是由頂點(diǎn)的有窮非空集合和頂點(diǎn)之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個(gè)圖,V 是圖 G 中頂點(diǎn)的集合,E 是圖 G 中邊的集合。
例如:圖 2.1 所示圖
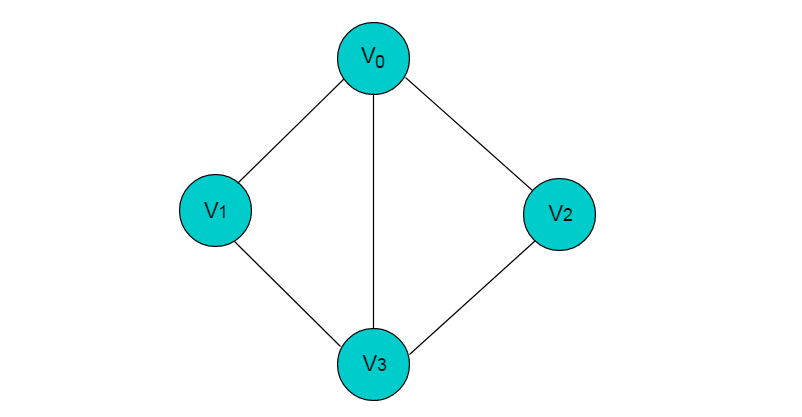
圖2.1
在圖 2.1 中,共有 V0,V1,V2,V3 這 4 個(gè)頂點(diǎn),4 個(gè)頂點(diǎn)之間共有 5 條邊。
注:
當(dāng)線(xiàn)性表沒(méi)有數(shù)據(jù)節(jié)點(diǎn)時(shí),線(xiàn)性表為空表。樹(shù)中沒(méi)有節(jié)點(diǎn)時(shí),樹(shù)為空樹(shù)。但是,在圖中不允許沒(méi)有頂點(diǎn),但是可以沒(méi)有邊。
2.2 無(wú)向邊
無(wú)向邊:若頂點(diǎn) x 和 y 之間的邊沒(méi)有方向,則稱(chēng)該邊為無(wú)向邊(x,y),(x,y) 與 (y,x) 意義相同,表示 x 和 y 之間有連接。??圖 2.2 所示圖中的邊均為無(wú)向邊。
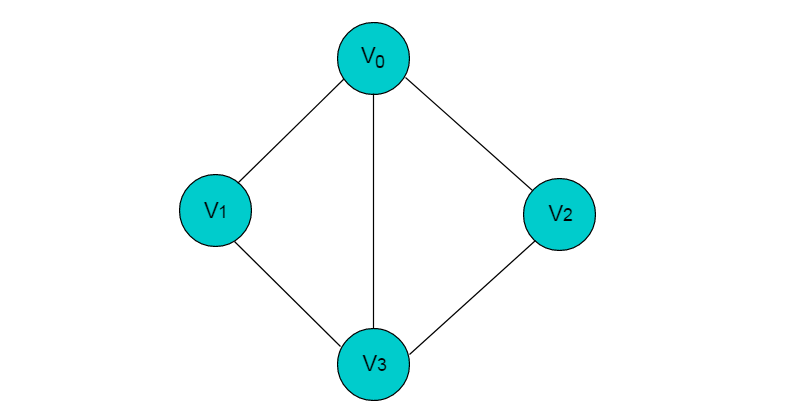
圖2.2
2.3 有向邊
有向邊:若頂點(diǎn) x 和 y 之間的邊有方向,則稱(chēng)該邊為有向邊,與表示的意義是不同的,表示從 x 連接到 y ,x 稱(chēng)為尾,y 稱(chēng)為頭。表示從 y 連接到 x ,y 稱(chēng)為尾, x 稱(chēng)為頭。??圖2.3所示圖中的邊為有向邊。
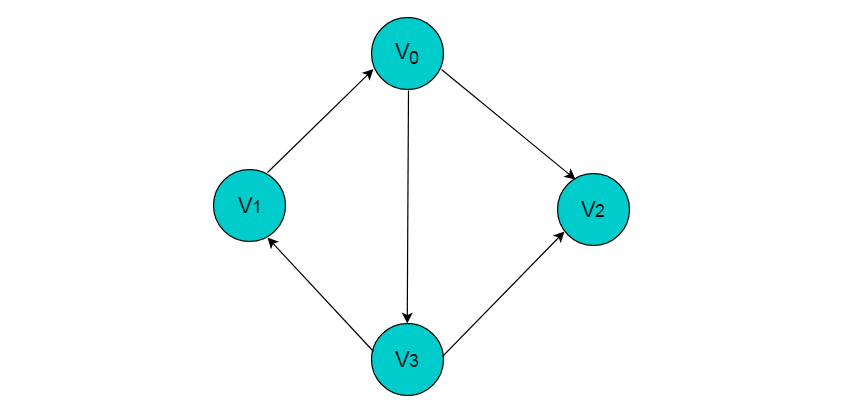
圖2.3
2.4 無(wú)向圖
無(wú)向圖:若圖中任意兩個(gè)頂點(diǎn)之間的邊均是無(wú)向邊,則稱(chēng)該圖為無(wú)向圖。圖2.2所示圖為無(wú)向圖。
2.5 有向圖
有向圖:若圖中任意兩個(gè)頂點(diǎn)之間的邊均是有向邊,則稱(chēng)該圖為有向圖。圖2.3所示的圖為有向圖。
2.6 頂點(diǎn)與頂點(diǎn)的度
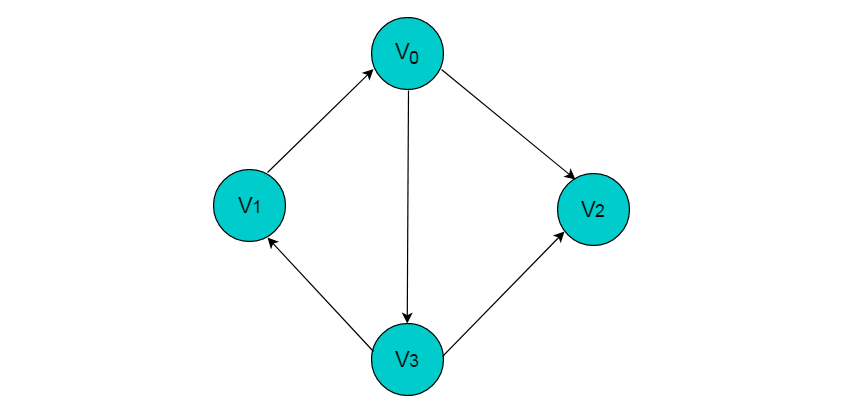
圖2.6
頂點(diǎn)的度:
頂點(diǎn) V 的度是和 V 相關(guān)聯(lián)的邊的數(shù)目,記為T(mén)D(V)。
圖 2.6 所示圖中,V0 頂點(diǎn)的度為 3 。
入度:
以頂點(diǎn)v為頭的邊的數(shù)目,記為ID(V)。
圖2.6所示圖中,V0的入度為1。
出度:
以頂點(diǎn) v 為尾的邊的數(shù)目,記為 OD(V)。
圖2.6所示圖中,V0的出度為2。
頂點(diǎn)的度 = 入度 + 出度。
即 TD(V) = ID(V) + OD(V)。
2.7 鄰接
鄰接是兩個(gè)頂點(diǎn)之間的一種關(guān)系。如果圖包含(u,v),則稱(chēng)頂點(diǎn) v 與頂點(diǎn) u 鄰接。在無(wú)向圖中,這也暗示了頂點(diǎn) u 也與頂點(diǎn) v 鄰接。換句話(huà)說(shuō),在無(wú)向圖中鄰接關(guān)系是對(duì)稱(chēng)的。
2.8 路徑
路徑:在圖中,依次遍歷頂點(diǎn)序列之間的邊所形成的軌跡。??例如:在圖 2.8 中所示圖中依次訪(fǎng)問(wèn)頂點(diǎn) V0 、V3 和 V2 ,則構(gòu)成一條路徑。
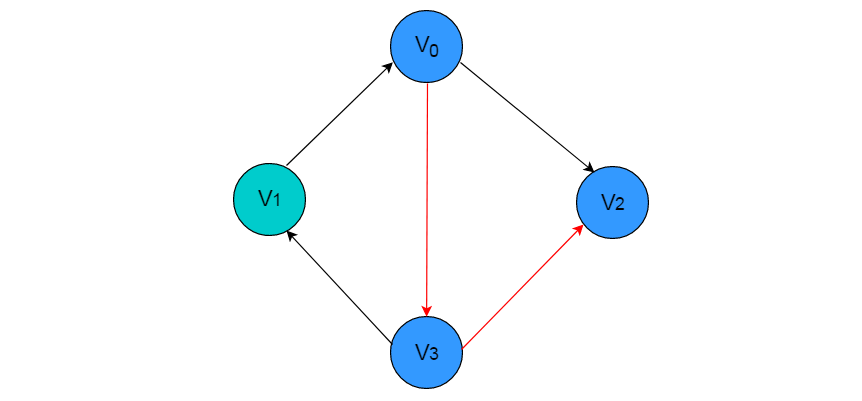
圖 2.8
3 完全圖
完全圖:每個(gè)頂點(diǎn)都與其他頂點(diǎn)相鄰接的圖。
無(wú)向完全圖:在無(wú)向圖中,如果任意兩個(gè)頂點(diǎn)之間都存在邊,則稱(chēng)該圖為無(wú)向完全圖。(含有n個(gè)頂點(diǎn)的無(wú)向完全圖有(n×(n-1))/2條邊)圖 3.1 所示的圖為無(wú)向完全圖。
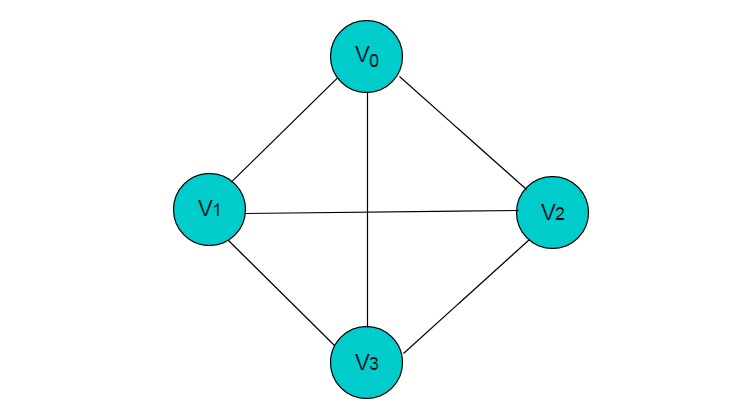
圖3.1
有向完全圖:在有向圖中,如果任意兩個(gè)頂點(diǎn)之間都存在方向互為相反的兩條邊,則稱(chēng)該圖為有向完全圖。(含有 n 個(gè)頂點(diǎn)的有向完全圖有 n×(n-1) 條邊)
圖3.2所示的圖為有向完全圖。
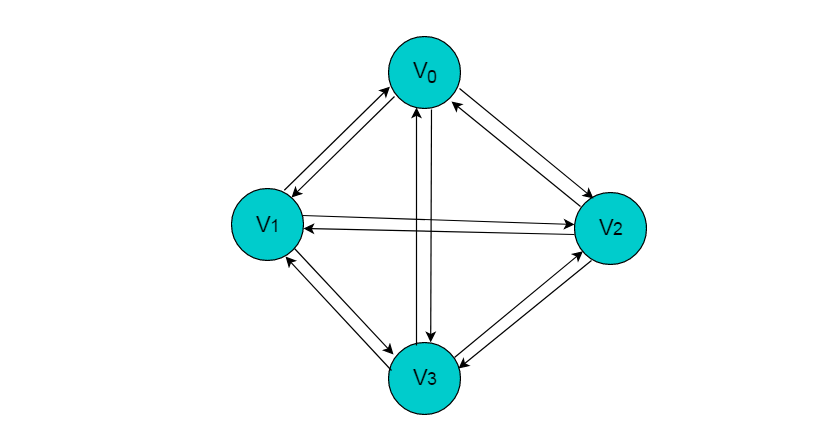
圖3.2
4 連通圖
在無(wú)向圖 G 中,如果從頂點(diǎn) v 到頂點(diǎn) v' 有路徑,則稱(chēng) v 和 v' 是連通的。 如果對(duì)于圖中任意兩個(gè)頂點(diǎn) vi 、vj ∈E, vi,和vj都是連通的,則稱(chēng) G 是連通圖,否則圖為非連通圖。??例如:圖4.1所示圖,圖中頂點(diǎn)A、B、C、D是連通的,但是其中任一頂點(diǎn)與頂點(diǎn)E或者頂點(diǎn)F之間沒(méi)有路徑,因此圖4.1中所示的圖為非連通圖。
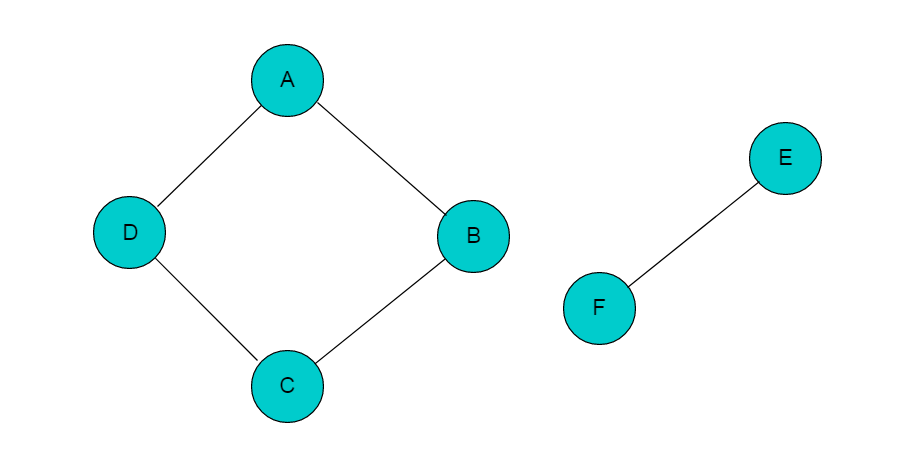
圖4.1
若添加頂點(diǎn)B與頂點(diǎn)F之間的鄰接邊,則圖變?yōu)檫B通圖,如圖4.2所示:
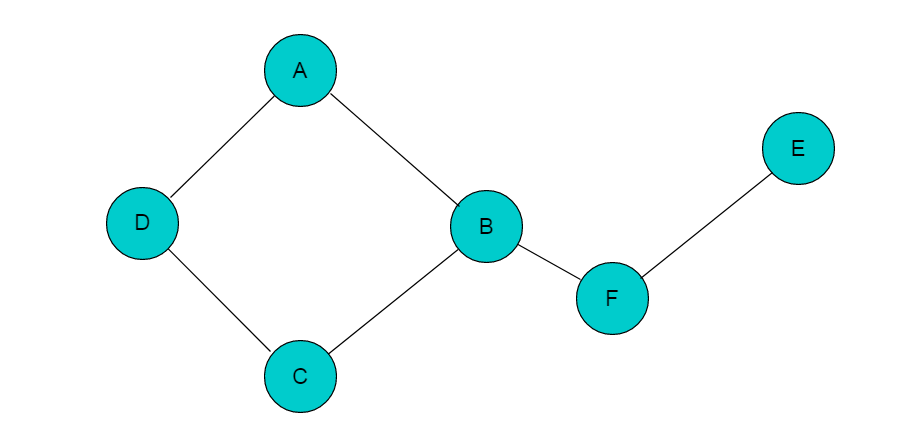
圖4.2
5 數(shù)組存儲(chǔ)
圖的數(shù)組存儲(chǔ)方式也稱(chēng)為鄰接矩陣存儲(chǔ)。圖中的數(shù)據(jù)信息包括:頂點(diǎn)信息和描述頂點(diǎn)之間關(guān)系的邊的信息,將這兩種信息存儲(chǔ)在數(shù)組中即為圖的數(shù)組存儲(chǔ)。??首先,創(chuàng)建頂點(diǎn)數(shù)組,頂點(diǎn)數(shù)組中存儲(chǔ)的是圖的頂點(diǎn)信息,采用一維數(shù)組的方式即可存儲(chǔ)所有的頂點(diǎn)信息。存儲(chǔ)圖中邊的信息時(shí),由于邊是描述頂點(diǎn)與頂點(diǎn)之間關(guān)系的信息,因此需要采用二維數(shù)組進(jìn)行存儲(chǔ)。
定義:設(shè)圖 G 有 n 個(gè)頂點(diǎn),則鄰接矩陣是一個(gè)n X n的方陣A,定義為:

圖 5 其中,或者(Vi , Vj,)表示頂點(diǎn) Vi 與頂點(diǎn) Vj 鄰接。wi,j表示邊的權(quán)重值。
例如:下圖所示的無(wú)向圖,采用數(shù)組存儲(chǔ)形式如下。
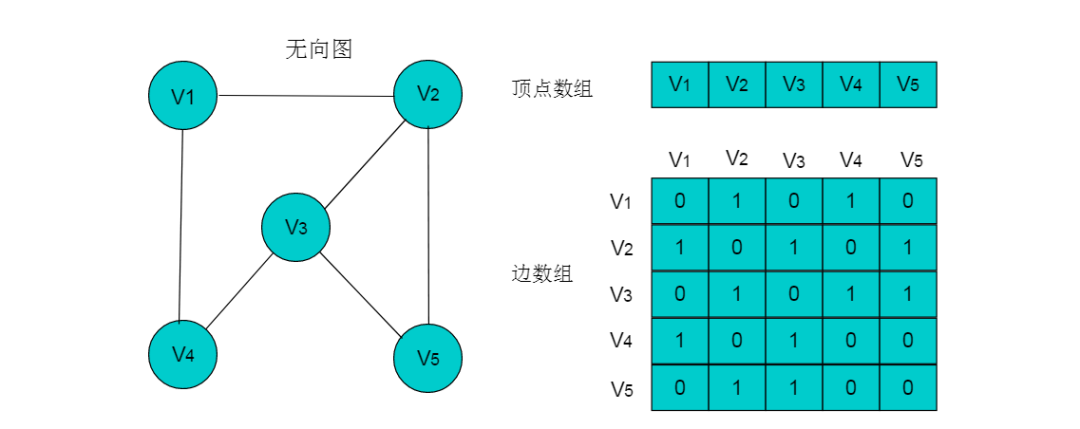
圖5.1
注:圖中的數(shù)組存儲(chǔ)方式簡(jiǎn)化了邊的權(quán)值為 1 。
無(wú)向圖的數(shù)組存儲(chǔ)主要有以下特性:
(1)頂點(diǎn)數(shù)組長(zhǎng)度為圖的頂點(diǎn)數(shù)目n。邊數(shù)組為n X n的二維數(shù)組。(2)邊數(shù)組中,A[i][j] =1代表頂點(diǎn)i與頂點(diǎn)j鄰接,A[i][j] = 0代表頂點(diǎn)i與頂點(diǎn)j不鄰接。(3)在無(wú)向圖中。由于邊是無(wú)向邊,因此頂點(diǎn)的鄰接關(guān)系是對(duì)稱(chēng)的,邊數(shù)組為對(duì)稱(chēng)二維數(shù)組。(4)頂點(diǎn)與自身之間并未鄰接關(guān)系,因此邊數(shù)組的對(duì)角線(xiàn)上的元素均為0。(5)頂點(diǎn)的度即為頂點(diǎn)所在的行或者列1的數(shù)目。例如:頂點(diǎn)V2的度為3,則V2所在行和列中的1的數(shù)目為3。
當(dāng)圖為有向圖時(shí),圖的數(shù)組存儲(chǔ)方式要發(fā)生變化。例如:圖5.2所示的有向圖,采用數(shù)組存儲(chǔ)形式如下。
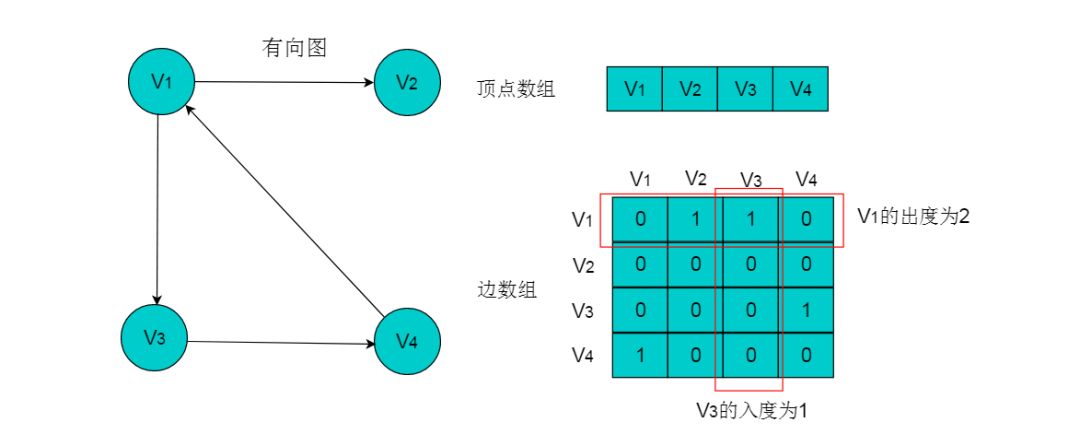
圖5.2
有向圖的數(shù)組存儲(chǔ)主要有以下特性:
(1)頂點(diǎn)數(shù)組長(zhǎng)度為圖的頂點(diǎn)數(shù)目n。邊數(shù)組為n X n的二維數(shù)組。(2)邊數(shù)組中,數(shù)組元素為1,即A[i][j] = 1,代表第i個(gè)頂點(diǎn)與第j個(gè)頂點(diǎn)鄰接,且i為尾,j為頭。 A[i][j] = 0代表頂點(diǎn)與頂點(diǎn)不鄰接。(3)在有向圖中,由于邊存在方向性,因此數(shù)組不一定為對(duì)稱(chēng)數(shù)組。(4)對(duì)角線(xiàn)上元素為0。(5)第i行中,1的數(shù)目代表第i個(gè)頂點(diǎn)的出度。例如:頂點(diǎn)V1的出度為2,則頂點(diǎn)V1所在行的1的數(shù)目為2。(6)第j列中,1的數(shù)目代表第j個(gè)頂點(diǎn)的入度。例如:V3的入度為1,則V3所在列中1的數(shù)目為1。
數(shù)組存儲(chǔ)方式優(yōu)點(diǎn):??數(shù)組存儲(chǔ)方式容易實(shí)現(xiàn)圖的操作。例如:求某頂點(diǎn)的度、判斷頂點(diǎn)之間是否有邊(弧)、找頂點(diǎn)的鄰接點(diǎn)等等。數(shù)組存儲(chǔ)方式缺點(diǎn):??采用數(shù)組存儲(chǔ)方式,圖若有n個(gè)頂點(diǎn)則需要n2個(gè)單元存儲(chǔ)邊(弧),空間存儲(chǔ)效率為O(n2)。 當(dāng)頂點(diǎn)數(shù)目較多,邊數(shù)目較少時(shí),此時(shí)圖為稀疏圖,這時(shí)尤其浪費(fèi)空間。??例如:圖5.3所示的圖,圖中有 9 個(gè)頂點(diǎn),邊數(shù)為10,需要 9X9 的二維數(shù)組,而實(shí)際存儲(chǔ)邊信息空間只有10,造成空間浪費(fèi)。
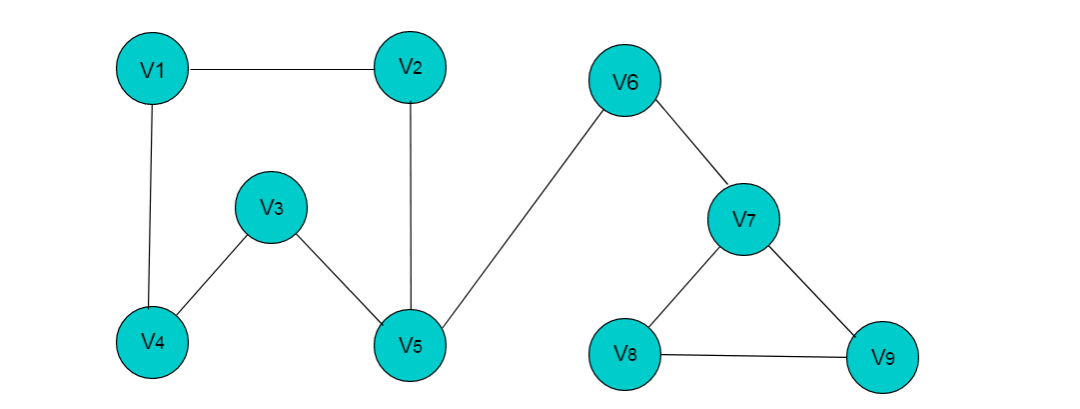
圖5.3
圖5.3所示無(wú)向圖的存儲(chǔ)數(shù)組:
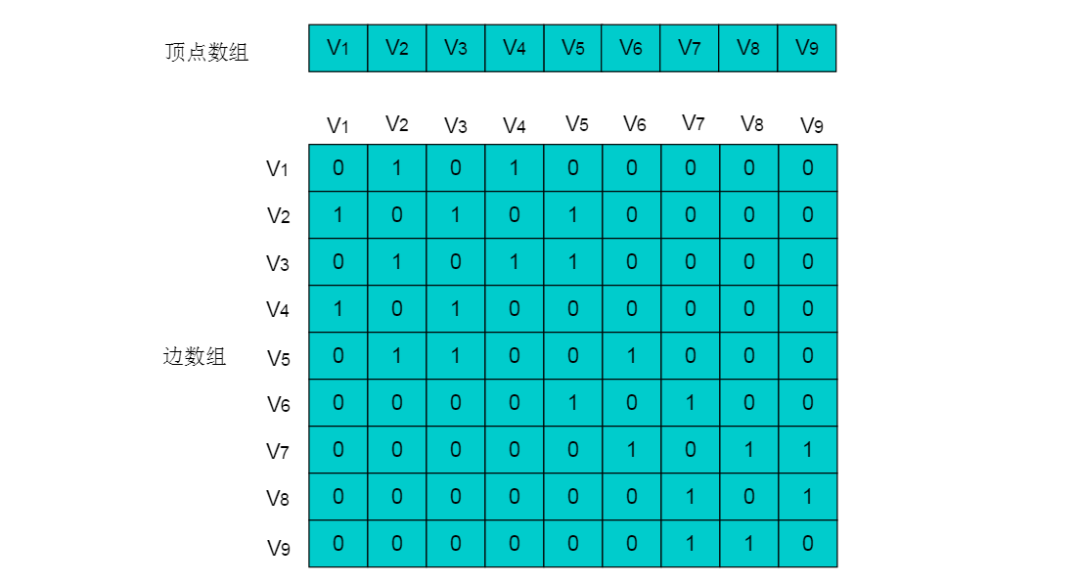
6 鄰接表
當(dāng)使用數(shù)組存儲(chǔ)時(shí),主要有以下三個(gè)問(wèn)題:
(1)對(duì)于一個(gè)圖,若圖中的頂點(diǎn)數(shù)目過(guò)大,則無(wú)法使用鄰接矩陣進(jìn)行存儲(chǔ)。因?yàn)樵诜峙鋽?shù)組內(nèi)存時(shí)可能會(huì)導(dǎo)致內(nèi)存分配失敗。(2)對(duì)于某些稀疏圖(即頂點(diǎn)數(shù)目多,邊數(shù)目少),創(chuàng)建的數(shù)組大小很大,而真正存儲(chǔ)的有用信息又很少,這就造成了空間上的浪費(fèi)。 (3)有時(shí)兩個(gè)點(diǎn)之間不止存在有一條邊,這是用鄰接矩陣就無(wú)法同時(shí)表示兩條以上的邊。
針對(duì)以上情況,提出了一種特殊的圖存儲(chǔ)方式,讓每個(gè)節(jié)點(diǎn)擁有的數(shù)組大小剛好就等于它所連接的邊數(shù),由此建立一種鄰接表的存儲(chǔ)方式。
鄰接表存儲(chǔ)方法是一種數(shù)組存儲(chǔ)和鏈?zhǔn)酱鎯?chǔ)相結(jié)合的存儲(chǔ)方法。在鄰接表中,對(duì)圖中的每個(gè)頂點(diǎn)建立一個(gè)單鏈表,第 i 個(gè)單鏈表中的結(jié)點(diǎn)依附于頂點(diǎn) Vi 的邊(對(duì)有向圖是以頂點(diǎn)Vi為尾的弧)。鏈表中的節(jié)點(diǎn)稱(chēng)為表節(jié)點(diǎn),共有 3個(gè)域,具體結(jié)構(gòu)見(jiàn)下圖:
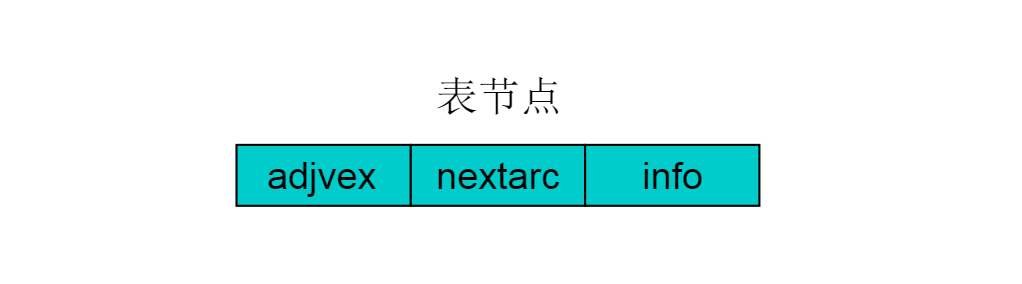
圖 6表結(jié)點(diǎn)由三個(gè)域組成,adjvex存儲(chǔ)與Vi鄰接的點(diǎn)在圖中的位置,nextarc存儲(chǔ)下一條邊或弧的結(jié)點(diǎn),data存儲(chǔ)與邊或弧相關(guān)的信息如權(quán)值。
除表節(jié)點(diǎn)外,需要在數(shù)組中存儲(chǔ)頭節(jié)點(diǎn),頭結(jié)點(diǎn)由兩個(gè)域組成,分別指向鏈表中第一個(gè)頂點(diǎn)和存儲(chǔ)Vi的名或其他信息。具體結(jié)構(gòu)如下圖:
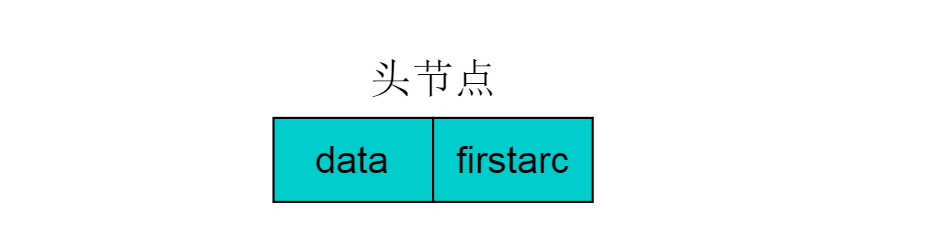
圖 6.0
其中,data域中存儲(chǔ)頂點(diǎn)相關(guān)信息,firstarc指向鏈表的第一個(gè)節(jié)點(diǎn)。無(wú)向圖采用鄰接表方式存儲(chǔ)例如:圖6.1所示的無(wú)向圖采用鄰接表存儲(chǔ)。
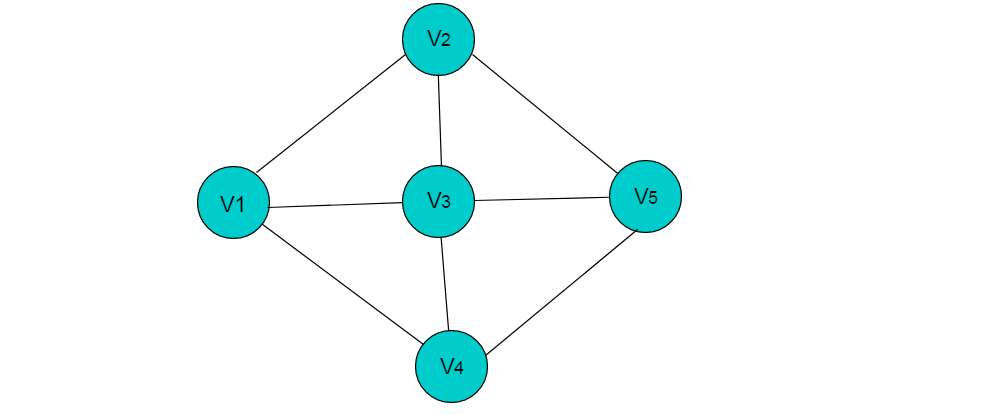
圖6.1 無(wú)向圖
采用鄰接表方式存儲(chǔ)圖 6.1 中的無(wú)向圖,繪圖過(guò)程中忽略邊節(jié)點(diǎn)的info信息,頭結(jié)點(diǎn)中的 data 域存儲(chǔ)頂點(diǎn)名稱(chēng)。以V1頂點(diǎn)為例,V1頂點(diǎn)的鄰接頂點(diǎn)為V2、V3、V4,則可以創(chuàng)建3個(gè)表節(jié)點(diǎn),表節(jié)點(diǎn)中adjvex分別存儲(chǔ)V2、V3、V4的索引1、2、3,按照此方式,得到的鄰接表為:
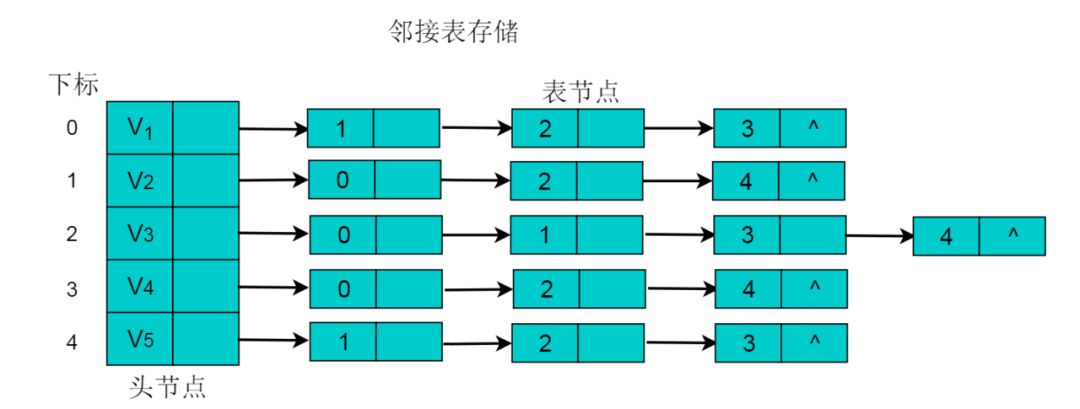
圖 6.2
無(wú)向圖的鄰接表存儲(chǔ)特性:
(1)數(shù)組中頭節(jié)點(diǎn)的數(shù)目為圖的頂點(diǎn)數(shù)目。(2)鏈表的長(zhǎng)度即為頂點(diǎn)的度。例如:V1頂點(diǎn)的度為3,則以V1為頭節(jié)點(diǎn)的鏈表中表節(jié)點(diǎn)的數(shù)目為3。
有向圖采用鄰接表方式存儲(chǔ)例如:圖 6.3 所示的有向圖采用鄰接表存儲(chǔ)。
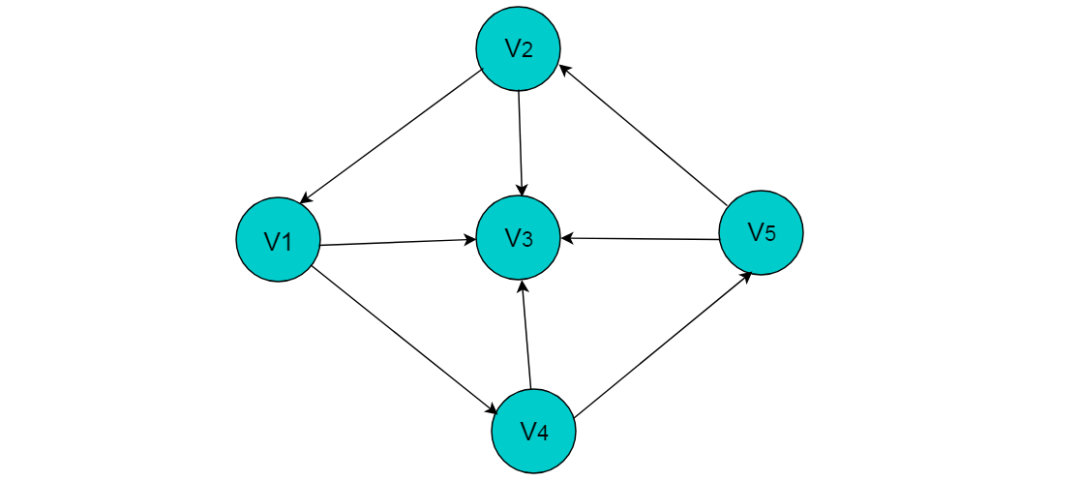
圖 6.3
采用鄰接表方式存儲(chǔ)圖6.3中的有向圖,繪圖過(guò)程中忽略邊節(jié)點(diǎn)的info信息,頭結(jié)點(diǎn)中的data域存儲(chǔ)頂點(diǎn)名稱(chēng)。以V1頂點(diǎn)為例,V1頂點(diǎn)的鄰接頂點(diǎn)為V2、V3、V4,但是以V1頂點(diǎn)為尾的邊只有兩條,即和因此,創(chuàng)建2個(gè)表節(jié)點(diǎn)。表節(jié)點(diǎn)中adjvex分別存儲(chǔ)V3、V4的索引2、3,按照此方式,得到的鄰接表為:
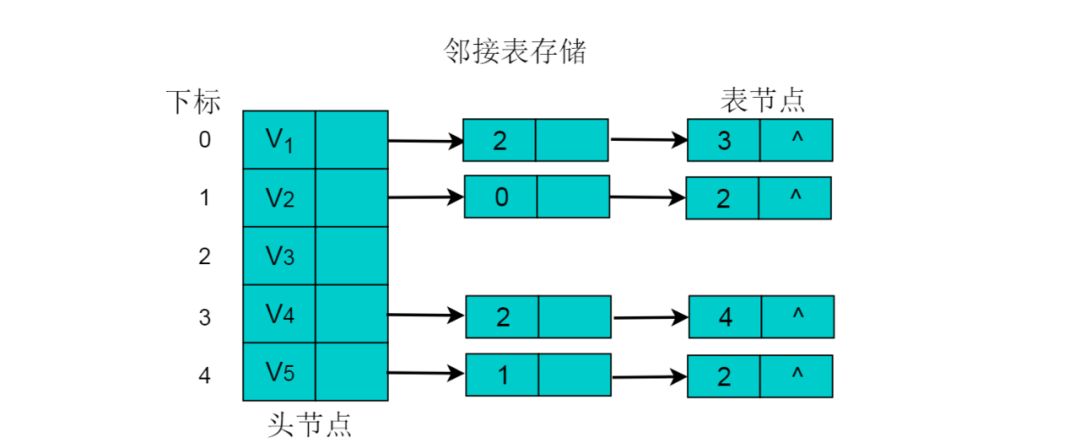
圖 6.4有向圖的鄰接表存儲(chǔ)特性:
(1)數(shù)組中表節(jié)點(diǎn)的數(shù)目為圖的頂點(diǎn)數(shù)目。(2)鏈表的長(zhǎng)度即為頂點(diǎn)的出度。例如V1的出度為2,V1為頭節(jié)點(diǎn)的鏈表中,表節(jié)點(diǎn)的數(shù)目為2。(3)頂點(diǎn)Vi的入度為鄰接表中所有adjvex值域?yàn)閕的表結(jié)點(diǎn)數(shù)目。例如:頂點(diǎn)V3的入度為4,則鏈表中所有adjvex值域?yàn)?的表結(jié)點(diǎn)數(shù)目為4。
注:圖采用鄰接表的方式表示時(shí),其表示方式是不唯一的。這是因?yàn)樵诿總€(gè)頂點(diǎn)對(duì)應(yīng)的單鏈表中,各邊節(jié)點(diǎn)的鏈接次序可以是任意的,取決于建立鄰接表的算法以及邊的輸入次序。
7 逆鄰接表
在鄰接表中,可以輕易的得出頂點(diǎn)的出度,但是想要得到頂點(diǎn)的入度,則需要遍歷整個(gè)鏈表。為了便于確定頂點(diǎn)的入度,可以建立有向圖的逆鄰接表。逆鄰接表的建立與鄰接表相反。??采用逆鄰接表的方式存儲(chǔ)圖3.2所示的無(wú)向圖。以V3頂點(diǎn)為例,V3頂點(diǎn)的鄰接頂點(diǎn)為V1、V2、V4、V5,以V3頂點(diǎn)為頭的邊有4條,即、、、因此,創(chuàng)建4個(gè)表節(jié)點(diǎn)。表節(jié)點(diǎn)中adjvex分別存儲(chǔ)V0、V1、V3、V4的索引0、1、3、4,按照此方式,得到的逆鄰接表為:
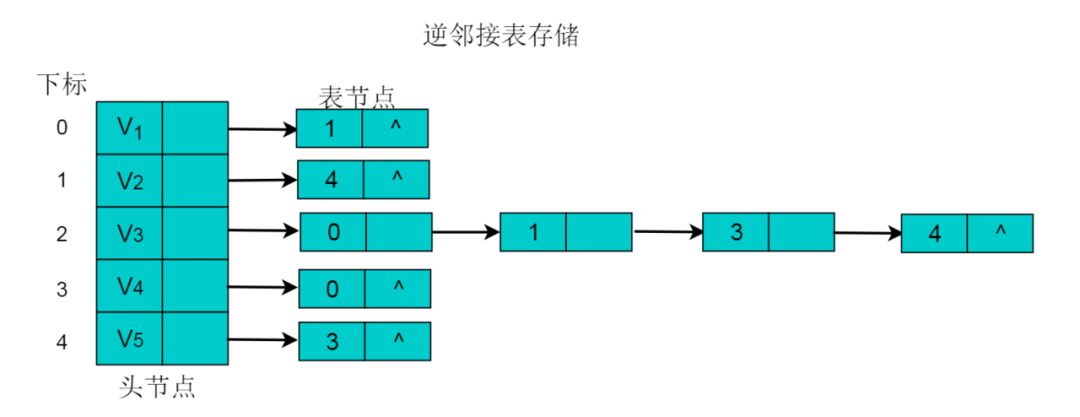
圖 7
8 十字鏈表
對(duì)于有向圖而言,鄰接鏈表的缺陷是要查詢(xún)某個(gè)頂點(diǎn)的入度時(shí)需要遍歷整個(gè)鏈表,而逆鄰接鏈表在查詢(xún)某個(gè)頂點(diǎn)的出度時(shí)要遍歷整個(gè)鏈表。為了解決這些問(wèn)題,十字鏈表將鄰接鏈表和逆鄰接鏈表綜合了起來(lái),而得到的一種十字鏈表。在十字鏈表中,每一條邊對(duì)應(yīng)一種邊節(jié)點(diǎn),每一個(gè)頂點(diǎn)對(duì)應(yīng)為頂點(diǎn)節(jié)點(diǎn)。
頂點(diǎn)節(jié)點(diǎn)頂點(diǎn)節(jié)點(diǎn)即為頭節(jié)點(diǎn),由3個(gè)域構(gòu)成,具體形式如下:

圖 8 其中,data域存儲(chǔ)與頂點(diǎn)相關(guān)的信息,firstin和firstout分別指向以此頂點(diǎn)為頭或尾的第一個(gè)邊節(jié)點(diǎn)。邊節(jié)點(diǎn)在邊節(jié)點(diǎn)為鏈表節(jié)點(diǎn),共有 5 個(gè)域,具體形式如下:

img 其中,尾域tailvex和頭域headvex分別指向尾和頭的頂點(diǎn)在圖中的位置。鏈域hlink指向頭相同的下一條邊,鏈域tlink指向尾相同的下一條邊。info 存儲(chǔ)此條邊的相關(guān)信息。例如:圖8.1所示的有向圖,采用十字鏈表存儲(chǔ)圖方式。
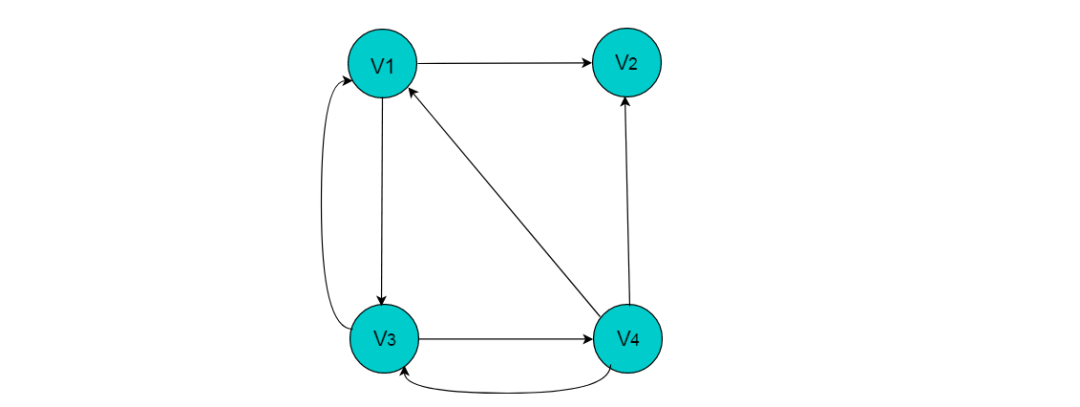
圖8.1 有向圖
采用十字鏈表的方式存儲(chǔ)圖8.1中的有向圖,繪圖過(guò)程忽略邊節(jié)點(diǎn)中的info信息,表頭節(jié)點(diǎn)中的data域存儲(chǔ)頂點(diǎn)名稱(chēng)。以V1頂點(diǎn)為例,頂點(diǎn)節(jié)點(diǎn)的data域存儲(chǔ)V1頂點(diǎn)名,firstin存儲(chǔ)以V1頂點(diǎn)為頭第一個(gè)邊節(jié)點(diǎn),以V1頂點(diǎn)為頭邊為,firstout存儲(chǔ)以以V1頂點(diǎn)為尾第一個(gè)邊節(jié)點(diǎn),對(duì)應(yīng)邊為。按照此規(guī)則,得到的十字鏈表存儲(chǔ)為:
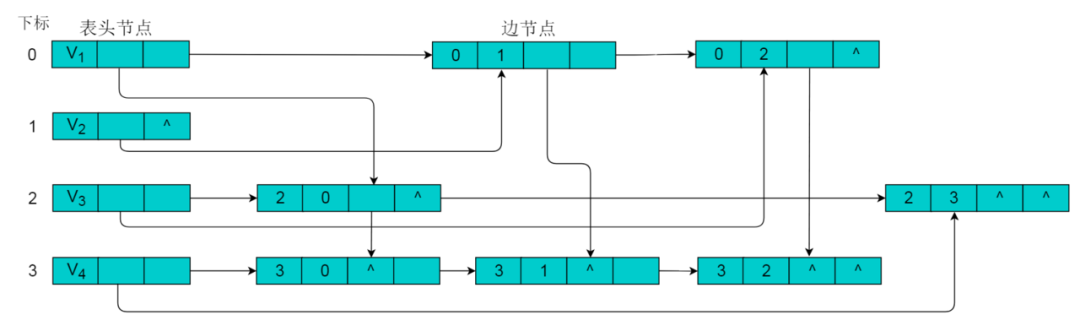
img注:采用十字鏈表存儲(chǔ)時(shí),表頭節(jié)點(diǎn)仍然使用數(shù)組存儲(chǔ),采用下標(biāo)索引方式獲取。
9 鄰接多重表
對(duì)于無(wú)向圖而言,其每條邊在鄰接鏈表中都需要兩個(gè)結(jié)點(diǎn)來(lái)表示,而鄰接多重表正是對(duì)其進(jìn)行優(yōu)化,讓同一條邊只用一個(gè)結(jié)點(diǎn)表示即可。鄰接多重表仿照了十字鏈表的思想,對(duì)鄰接鏈表的邊表結(jié)點(diǎn)進(jìn)行了改進(jìn)。
重新定義的邊結(jié)點(diǎn)結(jié)構(gòu)如下圖:

img 其中,ivex和jvex是指某條邊依附的兩個(gè)頂點(diǎn)在頂點(diǎn)表中的下標(biāo)。 ilink指向依附頂點(diǎn)ivex的下一條邊,jlink指向依附頂點(diǎn)jvex的下一條邊。info存儲(chǔ)邊的相關(guān)信息。
重新定義的頂點(diǎn)結(jié)構(gòu)如下圖:
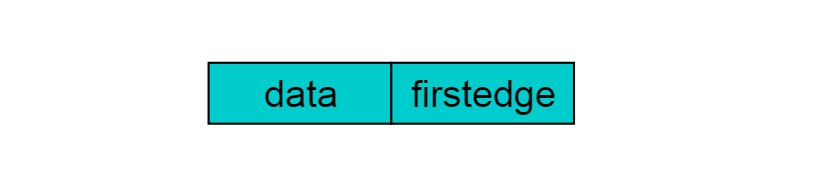
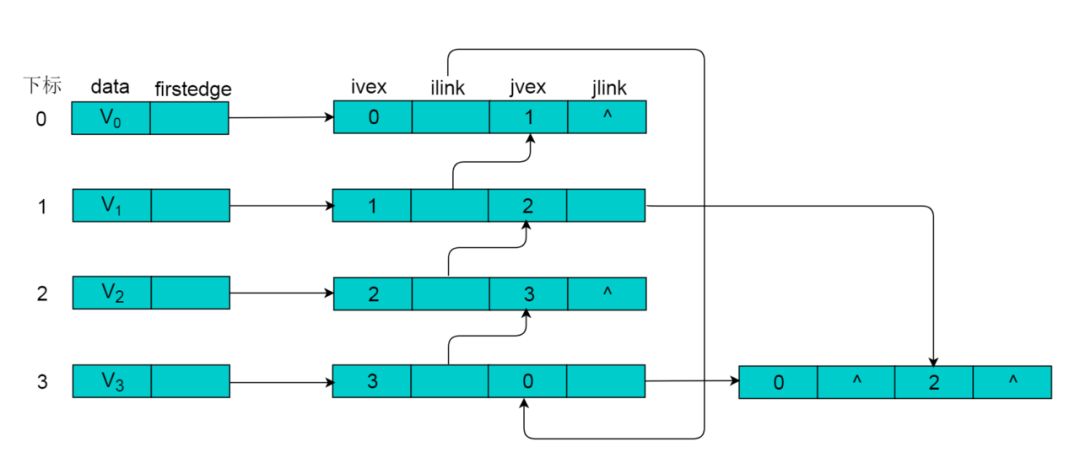
圖 9 其中,data存儲(chǔ)頂點(diǎn)的相關(guān)信息,firstedge指向第一條依附于該頂點(diǎn)的邊。例如:圖9.1所示的無(wú)向圖,采用鄰接多重表存儲(chǔ)圖。
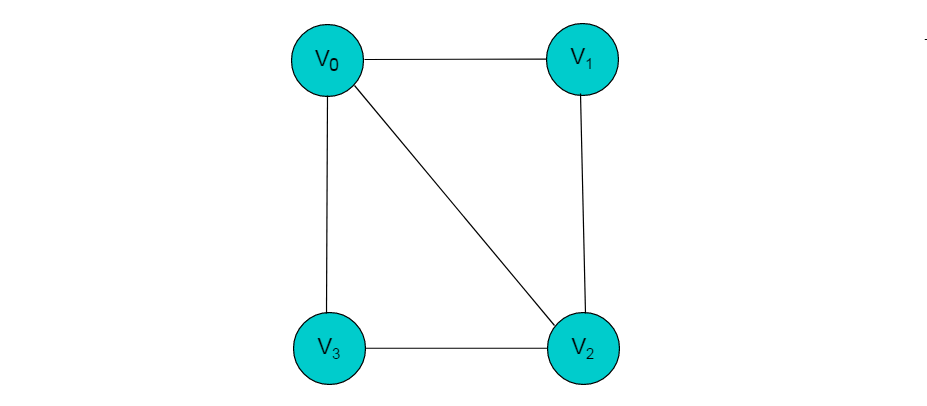
圖9.1 無(wú)向圖
圖 9.1 所示的無(wú)向圖,采用鄰接多重表存儲(chǔ),以 V0 為例,頂點(diǎn)節(jié)點(diǎn)的data域存儲(chǔ)V0名稱(chēng),firstedge 指向(V0 , V1)邊,邊節(jié)點(diǎn)中的ilink指向依附V0頂點(diǎn)的下一條邊(V0 , V3),jlink指向依附V1頂點(diǎn)的下一條邊(V1 , V2),按照此方式建立鄰接多重表:
-
算法
+關(guān)注
關(guān)注
23文章
4697瀏覽量
94715 -
數(shù)據(jù)存儲(chǔ)
+關(guān)注
關(guān)注
5文章
997瀏覽量
51610 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40596
原文標(biāo)題:數(shù)據(jù)結(jié)構(gòu)與算法——圖論基礎(chǔ)與圖存儲(chǔ)結(jié)構(gòu)
文章出處:【微信號(hào):TheAlgorithm,微信公眾號(hào):算法與數(shù)據(jù)結(jié)構(gòu)】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
單片機(jī) 數(shù)據(jù)結(jié)構(gòu) 算法 C語(yǔ)言 資料
常見(jiàn)的數(shù)據(jù)結(jié)構(gòu)
數(shù)據(jù)結(jié)構(gòu)與算法
數(shù)據(jù)結(jié)構(gòu)是什么_數(shù)據(jù)結(jié)構(gòu)有什么用
數(shù)據(jù)結(jié)構(gòu)與算法分析的C語(yǔ)言描述的電子教材詳細(xì)資料免費(fèi)下載
為什么要學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)?數(shù)據(jù)結(jié)構(gòu)的應(yīng)用詳細(xì)資料概述免費(fèi)下載
什么是數(shù)據(jù)結(jié)構(gòu)?為什么要學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)?數(shù)據(jù)結(jié)構(gòu)的應(yīng)用實(shí)例分析
大牛分享平時(shí)如何學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)與算法
計(jì)算機(jī)圖論算法的詳細(xì)資料說(shuō)明
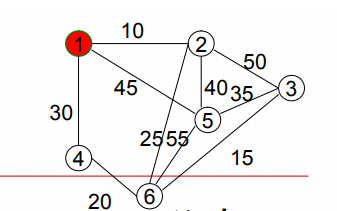
數(shù)據(jù)結(jié)構(gòu)教程之線(xiàn)性表的詳細(xì)資料說(shuō)明
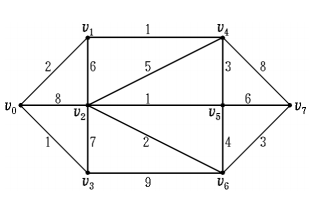
圖論算法及MATLAB程序代碼的詳細(xì)資料說(shuō)明
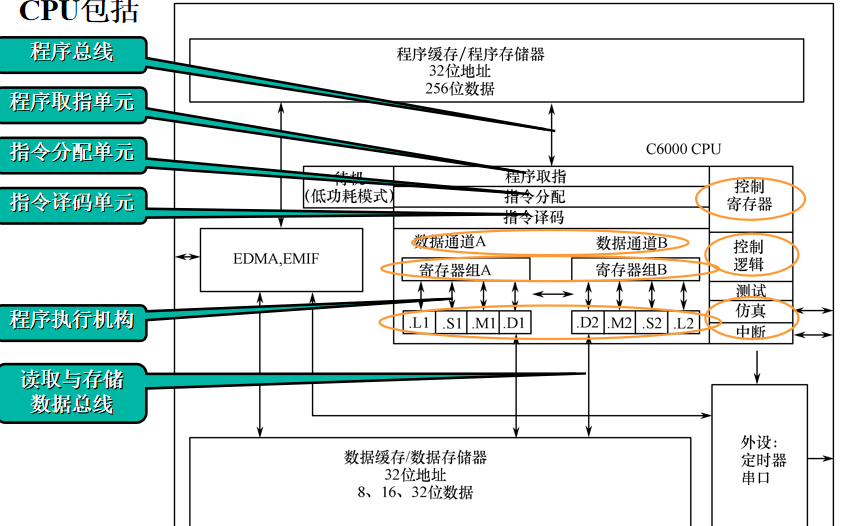
CPU結(jié)構(gòu)與指令集的詳細(xì)資料說(shuō)明
數(shù)據(jù)結(jié)構(gòu)與算法分析——Java語(yǔ)言描述
算法和數(shù)據(jù)結(jié)構(gòu)基礎(chǔ)知識(shí)分享(中)





 數(shù)據(jù)結(jié)構(gòu)與算法中圖論基礎(chǔ)與圖存儲(chǔ)結(jié)構(gòu)的詳細(xì)資料說(shuō)明
數(shù)據(jù)結(jié)構(gòu)與算法中圖論基礎(chǔ)與圖存儲(chǔ)結(jié)構(gòu)的詳細(xì)資料說(shuō)明










評(píng)論