今天的文章會重點關(guān)注決定神經(jīng)網(wǎng)絡(luò)學(xué)習處理速度的因素，以及獲得預(yù)測的精確度，即優(yōu)化策略的選擇。我們會講解多種主流的優(yōu)化策略，研究它們的工作原理，并進行相互比較。

機器學(xué)習算法的優(yōu)化

優(yōu)化是尋找可以讓函數(shù)最小化或最大化的參數(shù)的過程。當我們訓(xùn)練機器學(xué)習模型時，我們通常會使用間接優(yōu)化，選擇一種特定的衡量尺度，例如精確度或查全率等可以表現(xiàn)模型解決方法表現(xiàn)的指標。但是我們現(xiàn)在進行優(yōu)化的是另一種不同的價值函數(shù)J(θ)，希望通過將它的值最小化后，提高目標指標的表現(xiàn)。當然，價值函數(shù)的選擇通常和正在解決的問題有關(guān)，更重要的是，它通常表示我們距離理想解決方案的距離。可以想象，這一話題非常復(fù)雜。

優(yōu)化算法的可視化

陷阱無處不在

通常，找到非凸價值函數(shù)的最小值并不容易，我們必須用高級的優(yōu)化策略定位它們。如果你學(xué)過微積分，你會了解“局部最小值”的定義——這可能是優(yōu)化器最容易陷入的陷阱。此類情景的例子可以從上圖左邊看到，可以清楚地發(fā)現(xiàn)，優(yōu)化器定位的點并不是最優(yōu)解。

想克服所謂的“鞍點”問題會更困難。在水平處，價值函數(shù)的值幾乎是常數(shù)，上圖右側(cè)體現(xiàn)了這一問題，在這些點上，梯度在各個方向上幾乎為零，所以很難逃脫。

有時，尤其是在多層網(wǎng)絡(luò)中，我們要處理的價值函數(shù)可能很陡。在這種區(qū)域，梯度的值可能會急劇增加，即形成梯度爆炸，導(dǎo)致巨大的步長。但是這一問題可以通過梯度裁剪（gradient clipping）避免。

梯度下降

在了解高級算法之前，先讓我們看看基礎(chǔ)算法。也許最直接的方法之一就是向梯度的相反方向發(fā)展。這一策略可以用以下公式表示：

其中α是一個稱為學(xué)習速率的超參數(shù)，是每次迭代中采取的步長長度。在某種程度上，它的選擇表示了在學(xué)習速度和精確度之間的權(quán)衡。選擇的步長太小就會導(dǎo)致繁瑣的計算，不可避免地會進行多次迭代。但是，選擇的值過大，又無法找到最小值。如下圖所示，我們可以看到在相鄰的兩次迭代上是如何變化的，而不是趨于穩(wěn)定。同時，如果模型確定了合適的步長，可能會立刻找到一個最小值。

低學(xué)習率和高學(xué)習率下梯度下降

除此之外，算法還對“鞍點”問題很脆弱，因為在連續(xù)迭代中的修正尺寸對計算梯度是成比例的，這樣的話，就無法從平坦處逃脫。

最后，重點是這種算法并不高效，它在每次迭代中都需要用全部的訓(xùn)練集。這意味著，在每個epoch中我們都要查看所有樣本，從而在下次進行優(yōu)化。如果只有幾千個樣本還好，但如果有上百萬個樣本呢？在這種情況下，很難想象每次迭代需要花費多少時間

mini-batch梯度下降

梯度下降和mini-batch梯度下降對比

在這一部分，我們要重點解決梯度下降不高效的問題。雖然向量化處理加速了計算，當數(shù)據(jù)集有百萬個樣本時，可以一次性處理多個訓(xùn)練樣本。這里我們可以試試另一種方法，將整個數(shù)據(jù)集分成多個更小的批次（batch），用它們進行連續(xù)迭代。如上面動圖所示，由于每次處理的數(shù)據(jù)量更少了，新算法做決策的速度更快了。另外注意觀察模型之間動作的對比。梯度下降算法每一步都很長，且噪聲較小，而mini-batch梯度下降的步長更小，噪聲更大。甚至在mini-batch中，一次迭代可能會向相反方向發(fā)展。但是平均來說，都能達到最小值。

那么怎樣選擇batch size呢？在深度學(xué)習中，這類答案是不固定的，取決于要解決的案例。如果batch size等于整個數(shù)據(jù)集，那么處理起來就是普通的梯度下降。如果size為1，那么每次迭代禁止數(shù)據(jù)集的一個樣本。這種方法通常比較公平，常見的就是隨機梯度下降，它是通過選擇一個隨機數(shù)據(jù)集記錄，用它們當做訓(xùn)練集進行連續(xù)迭代。但是，如果我們決定使用mini-batch，通常會選擇一個中間值，通常是從64到512之間的樣本中選擇。

指數(shù)加權(quán)平均

這一概念在統(tǒng)計學(xué)或經(jīng)濟學(xué)中都有出現(xiàn)。很多高級神經(jīng)網(wǎng)絡(luò)優(yōu)化算法都用到了這一方法，因為它能在梯度為零的情況下依舊進行優(yōu)化。我們接下來以去年至今某大型科技公司的股票走勢為例進行講解。

不同β值下指數(shù)加權(quán)平均可視化

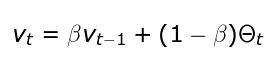
EWA主要是對之前的值進行平均，以便獨立考慮局部波動，并專注于整體趨勢。它的值使用上面的遞歸公式計算的，其中β適用于控制要平均的值的范圍參數(shù)。對于較大的β值，我們得到的圖形更平滑，因為記錄更多。

帶有動量的梯度下降

這一策略用指數(shù)加權(quán)平均避免了某一點處價值函數(shù)接近于0的可能。簡單來說，我們讓算法具有一定動量，所以即使局部梯度為0，我們?nèi)匀豢梢愿叽饲坝嬎愕闹迪蚯啊Ｋ赃@與純梯度下降相比是更好的方法。

通常，我們用反向傳播計算網(wǎng)絡(luò)中每一層dW和db的值。但是這一次，我們不直接用計算梯度更新神經(jīng)網(wǎng)絡(luò)參數(shù)的值，而是先計算VdW和Vdb的中間值。之后我們在梯度下降中用刀VdW和Vdb，過程如下公式所示：

如上文中股票的例子，指數(shù)加權(quán)平均可以讓我們專注于領(lǐng)先趨勢而不是噪聲。指示最小值的分量被放大，并且緩慢消除負責震蕩的分量。更重要的是，如果我們在后續(xù)更新中獲得指向類似方向的梯度，則學(xué)習率將增加。然而，這種方法有一個缺點：當你接近最小值時，動量值會增加，并且可能會變得很大，以至于算法無法再正確位置停止。

RMSProp

另一種提高梯度下降性能的方法就是使用RMSProp策略，這也是最常用的優(yōu)化算法之一。這也是另一種使用甲醛梯度下降的算法，并且它是可自適應(yīng)的，可以對模型每個參數(shù)調(diào)整學(xué)習率。后續(xù)參數(shù)的值取決于此前特殊參數(shù)上梯度的值。

但是，這種方法也有缺點，如上等式中的分母在每次迭代中增加，我們的學(xué)習率就會越來越小，結(jié)果可能導(dǎo)致模型完全停止。

優(yōu)化對比

Adam

最后的最后，我們來到了自適應(yīng)動量估計。這也是使用廣泛的算法，它吸取了RMSProp最大的優(yōu)點，將動量優(yōu)化的概念相結(jié)合，使得策略可以做出快速高效的優(yōu)化。

但是，盡管方法高效，計算的復(fù)雜程度也相應(yīng)上升。如上所示，我寫了十個矩陣等式，表示優(yōu)化過程中的單次迭代。可能很多人看起來都非常陌生。不要擔心！這些等式和此前的動量和RMSProp優(yōu)化算法相似。

結(jié)語

這篇文章對幾種優(yōu)化算法做了大致總結(jié)，了解這些算法有助于在不同情況下正確使用。