編者按：今天論智給大家帶來的論文是希伯來大學的Aharon Azulay和Yair Weiss近期發表的Why do deep convolutional networks generalize so poorly to small image transformations?這篇文章發現當小尺寸圖像發生平移后，CNN會出現識別錯誤的現象，而且這一現象是普遍的。

摘要

通常我們認為深度CNN對圖像的平移、形變具有不變性，但本文卻揭示了這樣一個現實：當圖像在當前平面上平移幾個像素后，現代CNN（如VGG16、ResNet50和InceptionResNetV2）的輸出會發生巨大改變，而且圖像越小，網絡的識別性能越差；同時，網絡的深度也會影響它的錯誤率。

論文通過研究表明，產生這個現象的主因是現代CNN體系結構沒有遵循經典采樣定理，無法保證通用性，而常用圖像數據集的統計偏差也會使CNN無法學會其中的平移不變性。綜上所述，CNN在物體識別上的泛化能力還比不上人類。

CNN的失誤

深度卷積神經網絡（CNN）對計算機視覺帶來的革新是天翻地覆的，尤其是在物體識別領域。和其他機器學習算法一樣，CNN成功的關鍵在于歸納偏差的方法，不同架構的選擇影響著偏差的具體計算方式。在CNN中，卷積和池化這兩個關鍵操作是由圖像不變性驅動的，這意味如果我們對圖像做位移、縮放、變形等操作，它們對網絡提取特征沒有影響。

但事實真的如此嗎？

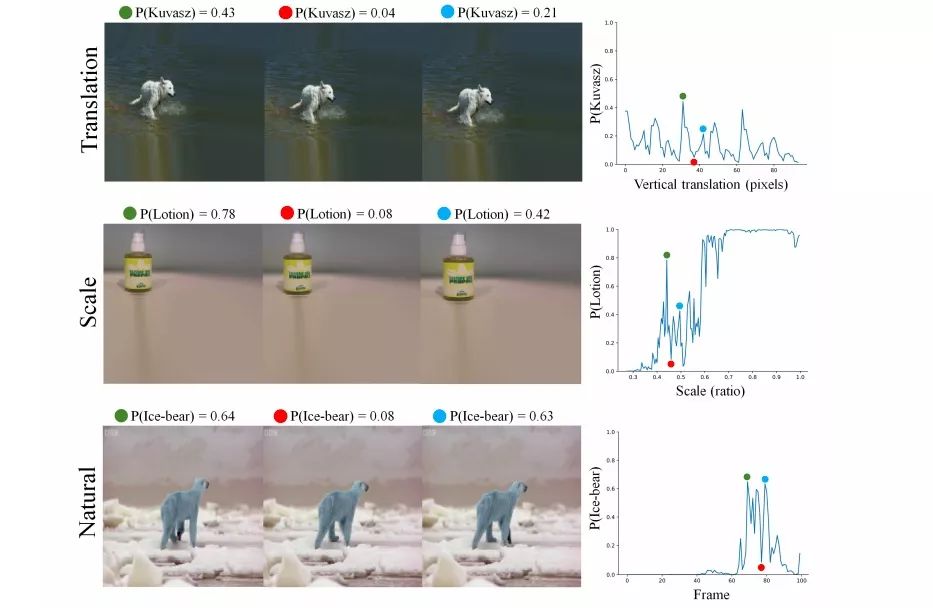
在上圖中，左側圖像是模型的輸入，右側折線圖是模型評分，使用的模型是InceptionResNet-V2 CNN。可以發現，作者在這里分別對圖像做了平移、放大和微小形變。在最上方的輸入中，他們只是將圖像從左到右依次下移了一像素，就使模型評分出現了劇烈的波動；在中間的輸入中，圖像被依次放大，模型的評分也經歷了直線下降和直線上升；而對于最下方的輸入，這三張圖是從BBC紀錄片中選取的連續幀，它們在人類眼中是北極熊的自然運動姿態，但在CNN“眼中”卻很不一樣，模型評分同樣遭遇“滑鐵盧”。

為了找出導致CNN失誤的特征，他們又從ImageNet驗證集中隨機選擇了200幅圖像，并把它們嵌入較大的圖像中做系統性平移，由圖像平移導致的空白區域已經用程序修補過了，在這個基礎上，他們測試了VGG16、ResNet50和InceptionResNetV2三個現代CNN模型的評分，結果如下：

圖A的縱坐標是200張圖像，它用顏色深淺表示模型識別結果的好壞，其中非黑色彩表示模型存在能對轉變后的圖像正確分類的概率，全黑則表示完全無法正確分類。通過觀察顏色變化我們可以發現，無論是VGG16、ResNet50還是InceptionResNetV2，它們在許多圖片上都顯示出了由淺到深的突然轉變。

論文作者在這里引入了一種名為jaggedness的量化標準：模型預測準確率top-5類別中的圖像，經歷一次一像素平移就導致分類錯誤（也可以是準確率低一下子變成準確率高）。他們發現平移會大幅影響輸出的圖片占比28%。而如圖B所示，相對于VGG16，ResNet50和InceptionResNetV2因為網絡更深，它們的“jaggedness”水平更高。

那么，這是為什么呢？

對采樣定理的忽略

CNN的上述失誤是令人費解的。因為從直觀上來看，如果網絡中的所有層都是卷積的，那當網絡對圖像編碼時，所有表征應該也都跟著一起被編碼了。這些特征被池化層逐級篩選，最后提取出用于分類決策的終極特征，理論上來說，這些特征相對被編碼的表征應該是不變的。所以問題在哪兒？

這篇論文提出的一個關鍵思想是CNN存在采樣缺陷。現代CNN中普遍包含二次采樣（subsampling）操作，它是我們常說的降采樣層，也就是池化層、stride。它的本意是為了提高圖像的平移不變性，同時減少參數，但它在平移性上的表現真的很一般。之前Simoncelli等人已經在論文Shiftable multiscale transforms中驗證了二次采樣在平移不變性上的失敗，他們在文中說：

我們不能簡單地把系統中的平移不變性寄希望于卷積和二次采樣，輸入信號的平移不意味著變換系數的簡單平移，除非這個平移是每個二次采樣因子的倍數。

考慮到現在CNN通常包含很多池化層，它們的二次采樣因子會非常大，以InceptionResnetV2為例，這個模型的二次采樣因子是45，所以它保證精確平移不變性的概率有多大？只有1/452。

下面我們從計算角度看看其中的貓膩：

我們設r(x)是模型在圖像x處獲得的特征信號，如果把圖像平移δ后，模型獲得的還是同樣的特征信號，那我們就稱這個信號是“卷積”的。注意一點，這個定義已經包含輸入圖像進入filter提取特征信號等其他線性操作，但不包括二次采樣和其他非線性操作。

觀察

如果r(x)是卷積的，那么全局池化后得到的特征信號 r = ∑xr(x) 應該具有平移不變性。

證明

以下論證來自之前我們對“卷積”的定義。如果r(x)是圖像x處的特征信號，而r2(x)是同一圖像平移后的特征信號，那么 ∑xr(x) = ∑xr2(x) 成立，因為兩者是平移前后的特征信號，是不變的。

定義

對于特征信號r(x)和二次采樣因子s，如果信號中x處的任意輸出x是采樣網格的線性插值：

那么我們就認為r(x)是“可位移的”（shiftable）。因為參照之前圖像位移的說法，既然采樣后信號具有平移不變性，那原信號載體就是可以移動的。其中xi是二次采樣因子s采樣網格上的信號，Bs(x)是從采樣中重建的r(x)基函數。

經典Shannon-Nyquist定理告訴我們，當且僅當采樣頻率是r(x)最高頻率的兩倍時，r(x)才可以位移。

論點

如果r(x)可以位移，那么采樣網格全局池化后得到的最終特征信號 r = ∑ir(xi) 應該具有平移不變性。

證明

通過計算我們發現了這么一個事實：采樣網格上的全局池化就相當于所有x的全局池化：

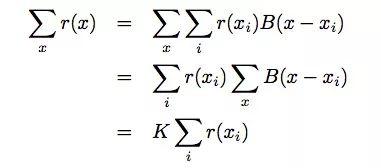
其中，K = ∑xB(x ? xi)和K與xi無關。

而現代CNN的二次采樣忽視了以上這些內容，所以平移不變性是難以保證的。

為什么CNN不能從數據中學習平移不變性？

雖然上一節論證了CNN在架構上就無法保證平移不變性，但為什么它就不能從大量數據里學到不變性呢？事實上，它確實能從數據中學到部分不變性，那么問題還出在哪兒？

論文的觀點是數據集里的圖像自帶“攝影師偏差”，很可惜論文作者做出的解釋很糟糕，一會兒講分布，一會兒講數據增強，非常沒有說服力。但是這個觀點確實值得關注，心理學領域曾有過關于“攝影師偏差”對人類視角影響的研究，雖然缺乏數據集論證，但很多人相信，同樣的影響也發生在計算機視覺中。

這里我們引用Azulay和Weiss的兩個更有說服力的點：

CIFAR-10和ImageNet的圖片存在大量“攝影師偏差”，這使得神經網絡無需學會真實的平移不變性。宏觀來看，只要不是像素級別的編碼，世界上就不存在兩張完全一樣的圖像，所以神經網絡是無法學到嚴格的平移不變性的，也不需要學。

例如近幾年提出的群卷積，它包含的filter數量比其他不變性架構更少，但代價是filter里參數更多，模型也更不靈活。如果數據集里存在“攝影師偏差”，那現有不變性架構里的參數是無法描述完整情況的，因此它們只會獲得一個“模糊”的結果，而且缺乏靈活性，性能自然也比非不變性架構要差不少。

小結

雖然CNN在物體識別上已經取得了“超人”的成果，但這篇論文也算是個提醒：我們還不能對它過分自信，也不能對自己過分自信。隨著技術發展越來越完善，文章中提及的這幾個本質上的問題也變得越來越難以蒙混過關。

或許由它我們能引出一個更有趣的問題，如果人類尚且難以擺脫由視覺偏差帶來的認知影響，那人類制造的系統、機器該如何超越人類意識，去了解真實世界。