最近看到一網友的一個問題,就是個不能再簡單的RLC網絡。那個帖子中的一個仿真見下圖:
通常,RLC網絡直接可以利用相量分析方法給出穩態解,如下圖:
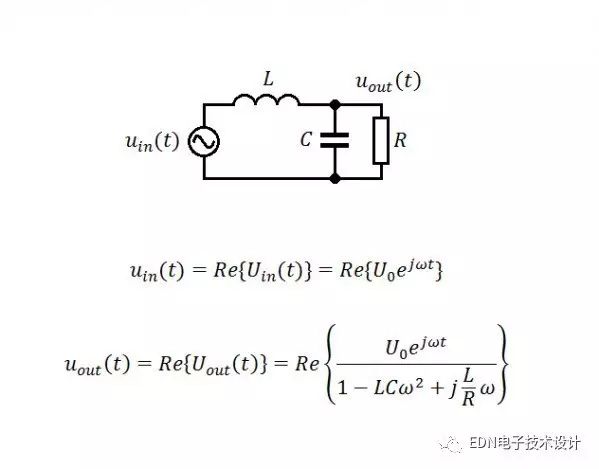
顯然,上面的那個相量方法所得的結果與首帖中的那個仿真相距甚遠。問題出在那里?
其實,相量分析的前提是單頻穩態,那就限制了許多的自由度。下面將考慮其它因素,采用拉普拉斯變換進行分析,見下圖:

拉普拉斯分析的最大特點就是考慮了系統的初始狀態,譬如圖中的V0(電容的初始電壓)和I0(電感的初始電流)。注意上圖中的兩個式子,上式給出了那個含初始狀態的RLC網絡的解,而下式則是采用了分部分式分解。對照相應的系數,可得下面的方程組:

由那個RLC網絡輸出響應式子,可直接看出所謂的“零狀態響應”和“零輸入響應”,見下式:

這些式子太簡單,不是本帖的主題。下面先看看那個仿真圖的情形,見下圖:

這是個零狀態響應,輸入為一個余弦電壓信號:Uin = U0 cos(ωt)注意,其響應是兩個等幅度但不同頻率的余弦信號的疊加,那就是首帖的仿真結果——差拍。
可能有人會問,拉普拉斯分析方法能否過渡到相量分析方法上去?當然可以,否則就不合理了。拉普拉斯分析中只要選擇適當的初始條件,就能使系統自身的“自然特性”不顯現出來,具體見下圖:

最后,需要特別指出的是,下式:

給出了其響應可以分解為系統自身特征和外部激勵特征這兩部分之和。顯見,如果存在電阻R(R≠∞),那么系統自身的自然特征部分將隨著時間推移呈指數衰減。最終趨近于相量分析法!
-
RLC
+關注
關注
1文章
116瀏覽量
39443 -
拉普拉斯變換
+關注
關注
1文章
32瀏覽量
10282
原文標題:就這么個RLC,你真的完全了解嗎?
文章出處:【微信號:edn-china,微信公眾號:EDN電子技術設計】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄





 RLC網絡直接可以利用相量分析方法給出穩態解
RLC網絡直接可以利用相量分析方法給出穩態解

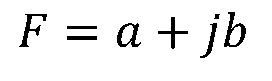










評論