編者按：和Daphne Cornelisse一起基于NumPy從頭搭建神經網絡，包含分步驟詳細講解，并在這一過程中介紹神經網絡的基本概念。

本文將介紹創建一個三層神經網絡所需的步驟。我將在求解問題的過程中，一邊和你解釋這一過程，一邊介紹一些最重要的概念。

需要求解的問題

意大利的一個農夫的標簽機出故障了：將三種不同品種的葡萄酒的標簽弄混了。現在剩下178瓶酒，沒人知道每瓶酒是什么品種！為了幫助這個可憐人，我們將創建一個分類器，基于葡萄酒的13個屬性識別其品種。

我們的數據是有標簽的（三種品種之一），這一事實意味著我們面臨的是一個監督學習問題。基本上，我們想要做的是使用我們的輸入數據（178瓶未分類的酒），通過神經網絡，輸出每瓶酒的正確標簽。

我們將訓練算法，使其預測每瓶酒屬于哪個標簽的能力越來越強。

現在是時候開始創建神經網絡了！

方法

創建一個神經網絡類似編寫一個非常復雜的函數，或者料理一道非常困難的菜肴。剛開始，你需要考慮的原料和步驟看起來很嚇人。但是，如果你把一切分解開來，一步一步地進行，會很順利。

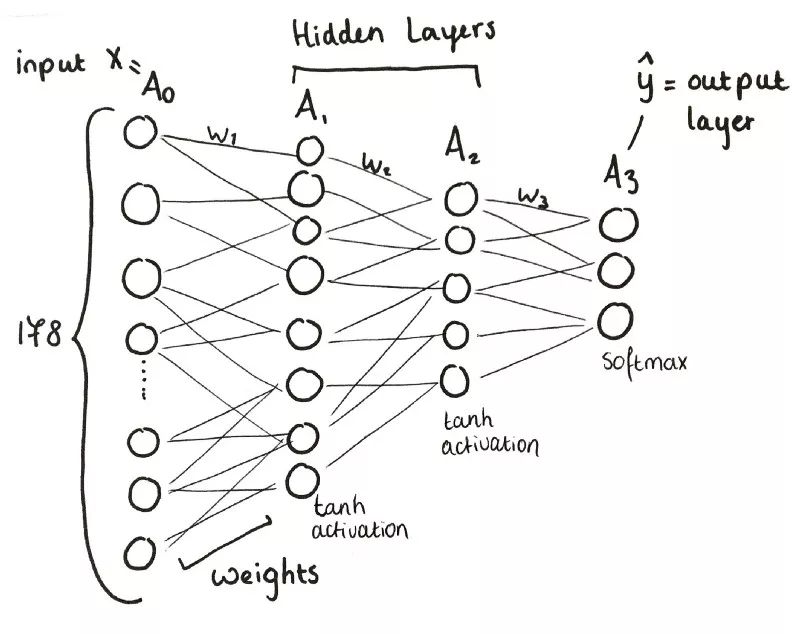
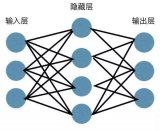
三層神經網絡概覽

簡單來說：

輸入層（x）包含178個神經元。

A1，第一層，包含8個神經元。

A2，第二層，包含5個神經元。

A3，第三層，也是輸出層，包含3個神經元。

第一步：預備

導入所有需要的庫（NumPy、scikit-learn、pandas）和數據集，定義x和y.

# 導入庫和數據集

import pandas as pd

import numpy as np

df = pd.read_csv('../input/W1data.csv')

df.head()

# Matplotlib是一個繪圖庫

import matplotlib

import matplotlib.pyplot as plt

# scikit-learn是一個機器學習工具庫

import sklearn

import sklearn.datasets

import sklearn.linear_model

from sklearn.preprocessing importOneHotEncoder

from sklearn.metrics import accuracy_score

第二步：初始化

在使用權重之前，我們需要初始化權重。由于我們目前還沒有用于權重的值，我們使用0到1之間的隨機值。

在Python中，random.seed函數生成“隨機數字”。然而，隨機數字并不是真隨機。這些生成的數字是偽隨機的，意思是，這些數字是通過非常復雜的公式生成的，看起來像是隨機的。為了生成數字，公式需要之前生成的值作為輸入。如果之前沒有生成過數字，公式常常接受時間作為輸入。

所以這里我們給生成器設置了一個種子——確保我們總是得到同樣的隨機數字。我們提供了一個固定值，這里我們選擇了零。

np.random.seed(0)

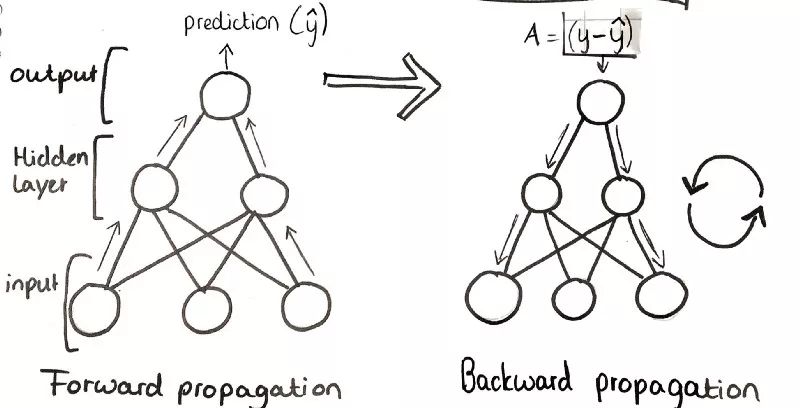
第三步：前向傳播

訓練一個神經網絡大致可以分為兩部分。首先，前向傳播通過網絡。也就是說，前向“步進”，并比較結果和真實值。

使用偽隨機數初始化權重后，我們進行一個線性的前向步驟。我們將輸入A0和隨機初始化的權重的點積加上一個偏置。剛開始，我們的偏置取值為0.

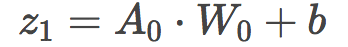
接著我們將z1（線性步驟）傳給第一個激活函數。激活函數是神經網絡中非常重要的部分。通過將線性輸入轉換為非線性輸出，激活函數給我們的函數引入了非線性，使它得以表示更復雜的函數。

有許多不同種類的激活函數（這篇文章詳細介紹了它們）。這一模型中，我們為兩個隱藏層——A1和A2——選擇了tanh激活函數，該函數的輸出范圍為-1到1.

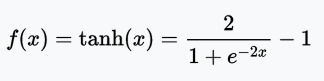
由于這是一個多類分類問題（我們有3個輸出標簽），我們將在輸出層A3使用softmax函數，它將計算分類的概率，也就是每瓶酒屬于3個分類的概率，并確保3個概率之和為1.

讓z1通過激活函數，我們創建了第一個隱藏層——A1——輸出值可以作為下一個線性步驟z2的輸入。

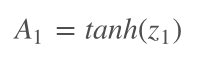
在Python中，這一步驟看起來是這樣的：

# 前向傳播函數

def forward_prop(model,a0):

# 加載模型參數

W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'], model['W3'],model['b3']

# 第一個線性步驟

z1 = a0.dot(W1) + b1

# 讓它通過第一個激活函數

a1 = np.tanh(z1)

# 第二個線性步驟

z2 = a1.dot(W2) + b2

# 讓它通過第二個激活函數

a2 = np.tanh(z2)

# 第三個線性步驟

z3 = a2.dot(W3) + b3

# 第三個激活函數使用softmax

a3 = softmax(z3)

# 保存所有計算所得值

cache = {'a0':a0,'z1':z1,'a1':a1,'z2':z2,'a2':a2,'a3':a3,'z3':z3}

return cache

第四步：反向傳播

正向傳播之后，我們反向傳播誤差梯度以更新權重參數。

我們通過計算誤差函數對網絡權重（W）的導數，也就是梯度下降進行反向傳播。

讓我們通過一個類比可視化這一過程。

想象一下，你在午后到山上徒步。過了一個小時后，你有點餓了，是時候回家了。唯一的問題是天變黑了，山上還有很多樹，你看不到家在何處，也搞不清楚自己在哪里。噢，你還把手機忘在家里了。

不過，你還記得你的房子在山谷中，整個區域的最低點。所以，如果你一步一步地沿著山勢朝下走，直到你感覺不到任何坡度，理論上你就到家了。

所以你就小心地一步一步朝下走。現在，將山想象成損失函數，將你想象成試圖找到家（即，最低點）的算法。每次你向下走一步，我們更新你的位置坐標（算法更新它的參數）。

山表示損失函數。為了得到較低的損失，算法沿著損失函數的坡度——也就是導數——下降。

當我們沿著山勢朝下走的時候，我們更新位置的坐標。算法更新神經網絡的權重。通過接近最小值，來接近我們的目標——最小化誤差。

在現實中，梯度下降看起來是這樣的：

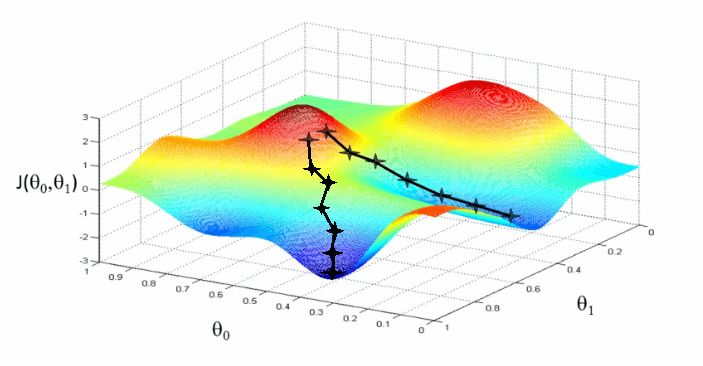
我們總是從計算損失函數的坡度（相對于線性步驟z）開始。

我們使用如下的記號：dv是損失函數對變量v的導數。

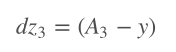
接著我們計算損失函數相對于權重和偏置的坡度。因為這是一個3層神經網絡，我們將在z3,2,1、W3,2,1、b3,2,1上迭代這一過程。從輸出層反向傳播到輸入層。

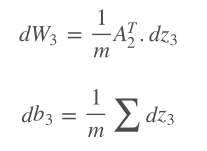
在Python中，這一過程是這樣的：

# 這是反向傳播函數

def backward_prop(model,cache,y):

# 從模型中加載參數

W1, b1, W2, b2, W3, b3 = model['W1'], model['b1'], model['W2'], model['b2'],model['W3'],model['b3']

# 加載前向傳播結果

a0,a1, a2,a3 = cache['a0'],cache['a1'],cache['a2'],cache['a3']

# 獲取樣本數

m = y.shape[0]

# 計算損失函數對輸出的導數

dz3 = loss_derivative(y=y,y_hat=a3)

# 計算損失函數對第二層權重的導數

dW3 = 1/m*(a2.T).dot(dz3)

# 計算損失函數對第二層偏置的導數

db3 = 1/m*np.sum(dz3, axis=0)

# 計算損失函數對第一層的導數

dz2 = np.multiply(dz3.dot(W3.T) ,tanh_derivative(a2))

# 計算損失函數對第一層權重的導數

dW2 = 1/m*np.dot(a1.T, dz2)

# 計算損失函數對第一層偏置的導數

db2 = 1/m*np.sum(dz2, axis=0)

dz1 = np.multiply(dz2.dot(W2.T),tanh_derivative(a1))

dW1 = 1/m*np.dot(a0.T,dz1)

db1 = 1/m*np.sum(dz1,axis=0)

# 儲存梯度

grads = {'dW3':dW3, 'db3':db3, 'dW2':dW2,'db2':db2,'dW1':dW1,'db1':db1}

return grads

第五步：訓練階段

為了達到可以給我們想要的輸出（三種葡萄酒品種）的最佳權重和偏置，我們需要訓練我們的神經網絡。

我認為這非常符合直覺。生活中幾乎每件事情，你都需要訓練和練習許多次，才可能擅長做這件事。類似地，神經網絡需要經歷許多個epoch或迭代，才可能給出精確的預測。

當你學習任何事情時，比如閱讀一本書，你都有一個特定的節奏。節奏不應該太慢，否則要花好些年才能讀完一本書。但節奏也不能太快，否則你可能會錯過書中非常重要的內容。

同理，你需要為模型指定一個“學習率”。學習率是更新參數時乘上的系數。它決定參數的變動有多快。如果學習率很低，訓練將花更多時間。然而，如果學習率太高，我們可能錯過極小值。

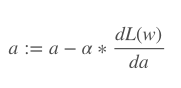
:=意味著這是一個定義，不是一個等式，或證明的結論。

a是學習率（稱為alpha）。

dL(w)是總損失對權重w的導數。

da是alpha的導數。

我們在一些試驗之后將學習率定為0.07.

# 這是我們最后返回的東西

model = initialise_parameters(nn_input_dim=13, nn_hdim= 5, nn_output_dim= 3)

model = train(model,X,y,learning_rate=0.07,epochs=4500,print_loss=True)

plt.plot(losses)

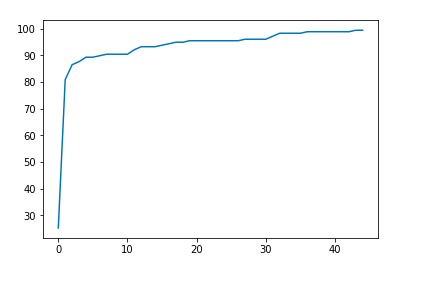
最后，這是我們的圖像。你可以繪制精確度和/或損失以得到預測表現的圖像。4500個epoch之后，我們的算法達到了99.4382022472 %的精確度。

簡短總結

我們從將數據傳入神經網絡開始，并對輸入數據逐層進行一些矩陣操作。在三個網絡層的每一層上，我們將輸入和權重的點積加上偏置，接著將輸出傳給選擇的激活函數。

激活函數的輸出接著作為下一層的輸入，并重復前面的過程。這一過程迭代三次，因為我們有三個網絡層。我們的最終輸出是哪瓶酒屬于哪個品種的預測，這是前向傳播過程的終點。

我們接著計算預測和期望輸出之間的差距，并在反向傳播過程中使用這一誤差值。

在反向傳播過程中，我們將誤差通過某種數學方式在網絡上進行反方向傳播。我們從錯誤中學習。

通過計算我們在前向傳播過程中使用的函數的導數，我們試圖發現我們應該給權重什么值，以做出盡可能好的預測。基本上，我們想要知道權重值和我們所得結果的誤差之間的關系。

在許多個epoch或迭代之后，神經網絡的參數逐漸適配我們的數據集，學習給出更精確的預測。

本文基于Bletchley Machine Learning訓練營第一周的挑戰。在這一訓練營中，我們每周討論一個不同的主題，并完成一項挑戰（需要真正理解討論的材料才能做到）。