近年來,隨著信息交互和數據共享的不斷增加,社交網絡的數量顯著提高。在分析此類網絡時,圖論提供了一個重要的建模模型。當節點代表用戶,邊表示互聯時,可以將此類網絡定義為一張圖,該圖中的節點可以是直接或間接相連的。在分析社交網絡數據時,定義和計算社區是最關鍵的步驟。同時,社區可以被看作是對整個網絡的概要表示(Summarization),因此,在社區檢測中需要使用這種概要設計理念。
當前對于社區網絡劃分研究已取得了很多研究成果,特別是社會網絡分析,但其仍然是一項具有挑戰性和吸引力的研究。因為在給定的圖中進行社區檢測,可以用于搜索潛在的合作者,用于優化社會關系,或在不同的社區中搜索一個關鍵人物等。
基于圖論的原理,已經提出了不少方法用來解決社區檢測的問題,如譜分析方法[6],其代表了一種非常特殊的社區檢測技術。這種方法的特殊性表現在其分類性能上,并以拉普拉斯矩陣的特征向量為基礎。使用這樣一個矩陣在時間和內存方面需要付出很高的代價。此外,在時間復雜度上,k個特征向量的計算復雜度為O(n3)。雖然,很容易計算出給定矩陣的特征向量,但是不方便計算大型拉普拉斯矩陣。這個方法的第二個缺點是假設社區的數量必須是已知的,但是在實際的大型社交網絡中很難獲得這一信息。文獻[7]提出了一種基于聚類概念的社區檢測方法。這種技術的優點是它能夠提供豐富的結果,使用這種方法發現的社區節點之間相互連接非常緊密。然而,在時間和內存方面代價很高,而且非常復雜。BASUCHOWDHURI P等人[8]提出了一種基于最大生成樹的并發方法。該方法使用共同鄰居的相似性作為邊的權重。將每個節點都與鄰居相連接,共享了大量的共同鄰居,從而建造了最大生成樹。與文獻[7]的方法相比較,這種方法在占用內存方面效果較好,但是其時間運行成本還是較高。文獻[9]提出了一種基于節點和邊的檢測社區方法,可廣泛用于查找網橋和服務供應商。但是,對于大型的社交網絡而言,這些方法的適用性均較差。
在以上文獻提出的方法中,運行時間的復雜度和內存的使用成本問題仍然存在。因此,它們的適用性具有一定的局限。為了解決這些問題,本文提出了一種有效的社區檢測算法方法,該方法基于聚類系數和共同鄰居指標。實驗結果表明,在大規模社會網絡數據集中提出的方法提供了較高質量的社區劃分結果,并具備線性運行時間的復雜度特性。
1 模型和指標定義
1.1 問題描述
在一個網絡模型中,一張圖G由有限集合(V,E)構成,其中V表示節點集合(網絡的用戶),E表示邊或節點之間相互聯系的集合,V={vi|i=1,…,n},E={eij|vi,vj∈V},n=|V|為節點總數,m=|E|為邊的總數。此外,當圖G′中節點的集合E′和邊的集合V′都是圖G中V和E的子集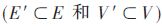 時,G′表示G的子圖。社交網絡可以建模為一個有向圖或一個無向圖,其中節點表示個體,邊表示節點之間的關系。本文重點是在社交網絡中進行社區檢測,它可以用一個無向圖來表示。這個社區可以被定義為節點的一個子集,與網絡的其他節點相比較,這些節點更有可能連接在一起。圖1顯示了一張具有3個社區的信息圖。
時,G′表示G的子圖。社交網絡可以建模為一個有向圖或一個無向圖,其中節點表示個體,邊表示節點之間的關系。本文重點是在社交網絡中進行社區檢測,它可以用一個無向圖來表示。這個社區可以被定義為節點的一個子集,與網絡的其他節點相比較,這些節點更有可能連接在一起。圖1顯示了一張具有3個社區的信息圖。

1.2 采用的度量標準
本文采用共同鄰居的相似性來衡量兩個節點的相似度,這意味著,當此度量指標較高時,節點更有可能是在同一個社區內。相比應用平均聚類系數來衡量集群的方法,本文提出的結果準確性更高。本文采用了兩種度量標準:
(1)共同鄰居的相似性:在參考文獻[8]和[10]中使用共同的鄰居來定義節點之間的相似性。如果兩個節點有大量的共同鄰居,那么它們更相似。這個指標由以下公式進行計算。

式中,A表示鄰居相似性。
(2)聚類系數:采用此類度量標準的目的是評估節點在一個集群中的集群化趨勢。其中最受歡迎的一個測量標準是模塊性最大化,但是它存在兩個問題:①它合并小型子圖,當分辨率較低時,它占主導地位;②它分裂大型子圖,當分辨率較高時,它占主導地位。另一種被廣泛使用的度量稱為聚類系數[10-11],在一個社區內提供了一個強大的鄰居結構。這項標準被廣泛應用于社會網絡分析中,它被定義為封閉的三聯體(三角形)數量和給定圖的三聯體數量之間的比率,式(2)給出了其定義[2]:

式中,C表示聚類系數。
2 提出的權重系數
本研究的目的是研究社區之間的邊所存在的一些性質,最后提取新的社區。
引理1:假設G是一張無向非加權圖,E表示G的邊集合,V表示G的節點集合,得到如下公式:

其中,L表示節點vi鄰居之間的關聯數量。
論證:假設G為一張圖,僅僅包含一個三角形T,本文假設它由3個節點組成(v1,v2,v3)。
如果計算L(v1),則發現一對關聯(v2和v3);如果計算v2的這一度量,則發現v1和v3之間的關聯;最后計算v3,得到了v1和v2之間的關聯。之后,如果計算總和L(v1)+L(v2)+L(v3),那么得到的結果是3對關聯。總之,當本文計算一張圖中每個節點與其鄰居之間的關聯數量時,對同一個三角形計算了3次。
圖2闡釋了一張無向圖,由7個節點和10條邊構成。該圖由3個三角形組成。當本文計算這7個節點鄰居之間的關聯數量總和時,得到表1所示結果。


根據這些結果,3個三角形共計算了3次,這意味著3×(在G1中的三角形數量)等于在G1中每個節點鄰居之間的關聯數量總和。
性質1:運用式(1),本文可以得出結論:兩個社區之間的一條邊的節點是不同的。它們沒有或僅有少數幾個共同的鄰居。
性質2:本文研究的重點在于在社區內最大化聚類系數(式(2))。為了達到這一目標,三角形的數量以及式(4)中的度量必須盡可能地最大化。實際上,在一個社區中每個節點鄰居之間的關聯數量必須最大化。這意味著對于具有較高聚類系數(大量三角形)的兩個社區之間的節點,其鄰居之間的關聯數量較大。
引理2:假設G是一張無向非加權的圖。在兩個社區之間一條邊e(vi,vj)的節點沒有或有幾個共同鄰居,節點vi和vj具有較高的度量L。
論據:通過使用性質1和性質2獲得引理2。
本文將節點鄰居之間的關聯數量標準化。由以下方程來定義標準化:

式中,B表示的是節點鄰居關聯數據標準。
通過式(1)可知節點之間共同鄰居的數量。從引理2可以得知,本文的目標是找到這些邊e(vi,vj),它們在鄰居i和j之間的關聯數量較大(見式(5)),而在i和j之間的共同鄰居數量較少(見式(1))。因此,以這些邊為基礎,所提方法的目標是找到度量W,W可以由如下公式定義:

3 本文提出的方法
在過去的幾年中,在社交網絡中進行社區檢測已經吸引了很多研究人員,但它仍是一項具有挑戰性的任務。事實上,大多數現有方法的適用性受限于它們的計算成本。本文提出的方法通過刪除在未加權圖中的社區之間的邊,從社交網絡中找到社區。本文假設一個社區必須至少有4個節點,如參考文獻[2]所使用的社區。刪除邊是為了最小化每條邊節點之間的共同鄰居數量(少于共同鄰居的20%),并且提高社區劃分的質量。下面介紹算法步驟和實例分析。
3.1 算法描述
本文提出的方法使用了以下步驟:
輸入:無向非加權的網絡G(V,E)
輸出:n個社區,Gs={Gs1,Gs2,…,Gsn}
(1)首先,本文計算在圖G中每個節點鄰居之間的關聯數量L(vi)。然后,本文計算每條邊e共同聚類數量C,以及這條邊的節點之間鄰居U的結合情況。之后,設L=L(vi)+L(vj)和S=|鄰居(vi)+鄰居(vj)|,其中vi、vj表示由邊e相連的兩個節點。

(2)本文使用W在表格T中以遞減順序對邊進行分類。一旦這個操作完成,就按照在T中的順序找到第一條邊e(vi,vj)。如果在刪除這條邊之后,vi鄰居的數量和vj鄰居的數量均會超過0,那么將這條邊從G中刪除,否則不刪除。本文需要對T中的其他邊重復測試,直到表格T是空為止。
(3)本文應用了一個社區必須至少包含4個節點的假設。為了確保該假設成立,需要把每張少于4個節點的子圖G′加入到在步驟(2)中已經被分離的最后一張子圖中。
3.2 實例分析
設一個網絡N1結構如圖3所示,圖4體現了提出的方法應用于網絡N1的結果。首先,運用步驟(1)在未加權的圖中計算每條邊的W值。然后,本文選擇符合以下條件的邊e(vi,vj):在節點vi和vj之間共同鄰居的數量較低(少于20%)。


本文運用W值對這些邊進行分類,按照遞減順序將這些邊儲存在表格T中。重復步驟(2)中邊的刪除操作,直到為空白為止。注意,大小小于2的群組不可以被分為獨立的群組。
最后,本文將少于4個節點的每張子圖G′加入到已經被分離的最后一張子圖中。
4 實驗結果與分析
為了驗證本算法的有效性,采用真實的較大規模社會網絡數據集進行實驗分析,并與生成樹算法[8]、CBCD算法[12]進行比較分析。
實驗環境中服務器設備參數為:Xeon E7-4820雙核處理器,2.5 GHz CPU頻率,16 GB內存,Windows Server 2012系統。本文在核心圖社區檢測時采用GN算法(Girvan-Newman)。
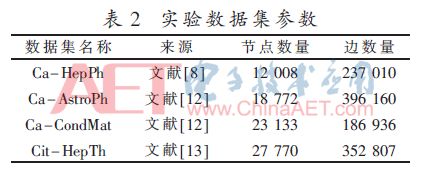
本文采用模塊性Q函數[13]來評價劃分出的模塊性,采用NMI[13]來評價劃分結果的相似性,兩個評價指標的數值越接近1,說明算法劃分的效果和質量越高。實驗采用的4個較大社會網絡數據集的具體參數如表2所示。
4.1 結果分析
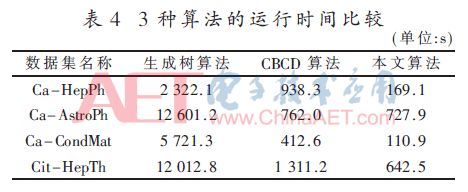
采用生成樹算法、CBCD算法和本文提出算法在以上4個社會網絡數據集上分別進行了100次運行測試,實驗結果的平均指標數據如表3所示。

通過表3可以看出,在Q函數指標結果上,本文提出算法比其他兩種算法都表現更好,即社會發現更有效,更好地體現了社區結構的劃分。在NMI指標結果上,相比其他兩種算法,本文算法的數值更接近于1,即劃分結果和真實的劃分更相似。
從表4中可以看出,本文算法在4個社會網絡數據集上的運行時間均比其他兩種算法少,即相比其他兩種算法,本算法具有更高的效率。
4.2 復雜度分析
該方法不是對所有的邊進行分類,而僅僅對共同鄰居少于20%的邊進行分類。例如,在Ca-CondMat網絡中,包含186 936條邊,本文僅僅對其中的67 297條邊進行分類。同樣,本文在Cit-HepTh網絡中僅僅對352 807條邊中的176 403條邊進行分類。
在步驟(2)中,本文對一部分共同鄰居少于20%的邊進行分類。如果本文假設這些邊的數量為k,那么復雜度為O(k·log(k)),即具有線性復雜度。在本算法的實施過程中,運用了python 3.3分類算法。如果假設在步驟(3)的操作之后發現子圖的數量為c,由少于4個節點構成的子圖數量為c1,那么復雜度為O(c1·log2(c))。因為O(c1·log2(c))<
5 結束語
本文提出了一種適用于社交網絡的新型社區檢測新方法。該方法使用了兩個最重要的度量來定義社區:(1)聚類系數,用于定義社區的質量;(2)屬于同一條邊的兩個節點共同鄰居的數量。實際上,與在不同社區中的兩個節點相比,在同一個社區中的兩個節點具有的共同鄰居數量較高。基于這些度量,本文推導出一個公式,允許在社區之間查找邊。在這個迭代的算法中,運用一些查找社區的標準來刪除邊。最后,實驗結果表明,與傳統的算法相比,本文提出的方法提供的網絡數據集合劃分不但模塊性高,NMI指標和運行效率也非常高。此外,該方法的運行時間具有線性復雜度,由此可以應用于大型的社交網絡中。
-
社交網絡
+關注
關注
0文章
48瀏覽量
3999
原文標題:【學術論文】基于非加權圖的大型社會網絡檢測算法研究
文章出處:【微信號:ChinaAET,微信公眾號:電子技術應用ChinaAET】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
矢量混頻器表征和混頻器測試系統矢量誤差修正的新方法 白皮書
基于LabVIEW8.2提取ECG特征點的新方法
運用于matlab中的矩陣求逆的新方法有哪些啊(不是函數inv)
使用電感式傳感的篡改攻擊低功耗檢測新方法
虛擬環境中軟體的包圍盒更新方法分析
采用小波包分析和擬同步檢波的電壓閃變信號檢測新方法
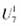
采用小波包分析和擬同步檢波的電壓閃變信號檢測新方法
基于平面陣列電磁傳感器的金屬缺陷檢測新方法






 適用于社交網絡的新型社區檢測新方法
適用于社交網絡的新型社區檢測新方法











評論