隨著人工智能系統(tǒng)在現(xiàn)實世界中扮演越來越重要的角色，理解不同的系統(tǒng)如何相互作用至關(guān)重要。

剛剛，DeepMind發(fā)表了一篇名為Symmetric Decomposition of Asymmetric Games的論文。在這篇論文中，DeepMind研究人員采用了博弈論的分支試圖這個問題。

研究人員重點觀察了在德州撲克，棋盤游戲蘇格蘭特警等非對稱博弈中，兩個智能體會有怎樣的行為和表現(xiàn)。

用這種新方法，智能體能簡單快速地在復(fù)雜的非對稱博弈里找到納什均衡。

博弈與納什均衡

博弈論屬于數(shù)學(xué)的一個分支，用于分析競爭環(huán)境下決策者的策略。

這套理論適用于人類，動物，以及超過一個AI時的多AI環(huán)境。比如說家里多個機(jī)器人同時打掃房間。

非對稱信息博弈模擬了真實世界的場景，就像拍賣時買家和賣家的心態(tài)和動機(jī)不同。我們得到的結(jié)果給了我們獨道的見解，以及極其簡潔的方式分析他們。

非對稱博弈的特點是每方玩家都有不同的策略、目標(biāo)和獎勵。比如說博弈論研究里最常見的協(xié)調(diào)博弈，性別之戰(zhàn)。

一般來說，多AI系統(tǒng)的進(jìn)化動態(tài)過程是用簡單的對稱博弈來分析，比如說經(jīng)典的囚徒困境，兩方玩家都可以采取同樣的行動。即使這些博弈能夠為多AI系統(tǒng)提供有效的洞見，告訴我們?nèi)绾尾僮魉型婕也拍塬@得最優(yōu)結(jié)果（這就是納什均衡），但他們并不能模擬出所有的情況。

DeepMind的新的方法，能簡單快速地在復(fù)雜的非對稱博弈里找到納什均衡。

雖然目前這套理論的重點還在如何應(yīng)用在多個AI系統(tǒng)的互動中，但研究人員相信這個結(jié)論也可以用于經(jīng)濟(jì)、進(jìn)化生物學(xué)、經(jīng)驗博弈論中。

歌劇還是電影？

舉個例子吧。

兩名玩家需要決定晚上是去看歌劇還是電影，不巧的是，其中一名偏好歌劇而另一名偏好電影。這是場不對稱的游戲，雖然兩名玩家可以任意選擇，但是根據(jù)玩家的喜好，每個玩家得到獎勵是不同的。

但是，為了維持他們的友誼，或者我們稱為一種平衡，雙方需要選擇相同的活動，因此單獨行動的回報為零。

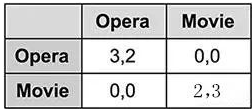
這個游戲有三個平衡：(i)雙方都去看歌劇，(ii)雙方去看電影，(iii)還有一個混合選項，每個玩家在五分之三的時間里選擇他們喜歡的選項。

這個“不穩(wěn)定的”的最后一個選項，就是用了將不對稱游戲簡化或分解成它的對稱對等體的方法。

我們可以將這種游戲的本質(zhì)想象成，每個玩家的獎勵分?jǐn)?shù)表是一個獨立對稱的雙玩家游戲，它的平衡點與原始的不對稱游戲一致。

在下面這張圖中，納什均衡是通過兩個對等點得到的，幫助我們快速確定不對稱博弈中的最優(yōu)策略(a)。反過來說，利用不對稱博弈來確定對稱對等點的均衡。

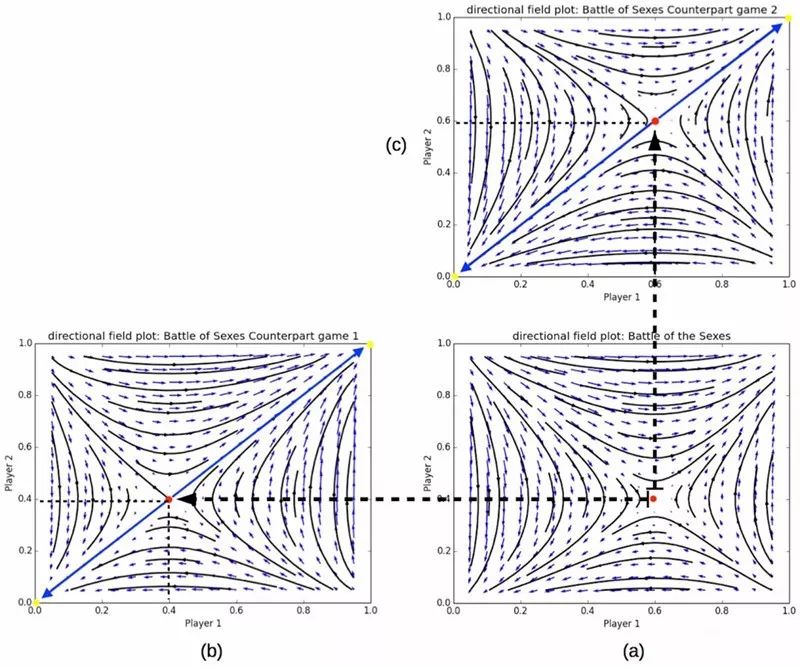
△紅點代表納什均衡。對于不對稱的游戲(a)，納什均衡可以很容易地從(b)和(c)兩張對稱圖中得到。上述圖中，x、y軸分別為玩家1、2選擇歌劇的概率

好消息是，這種方法也適用于其他游戲，比如Leduc撲克等。這些方法應(yīng)用了一個簡單的數(shù)學(xué)原理，從而快速直接分析不對稱游戲。我們希望它也能幫助我們理解各種動態(tài)系統(tǒng)，包括多代理環(huán)境。