微變等效電路和小信號等效電路是電子電路分析中兩種重要的等效電路方法。它們在電路設計和分析中有著廣泛的應用。本文將介紹微變等效電路和小信號等效電路的區(qū)別。
- 定義
微變等效電路(Microscopic Equivalent Circuit)是一種用于分析和設計電子電路的方法,它將電路中的元件視為微觀的物理實體,通過分析電路中各個元件的微觀行為來研究電路的整體性能。微變等效電路通常用于高頻、高速和大功率電路的分析和設計。
小信號等效電路(Small-Signal Equivalent Circuit)是一種用于分析和設計電子電路的方法,它將電路中的元件視為線性的、小信號的元件,通過分析電路中各個元件的小信號行為來研究電路的整體性能。小信號等效電路通常用于低頻、低功率和線性電路的分析和設計。
- 應用場景
微變等效電路主要應用于高頻、高速和大功率電路的分析和設計。這些電路中的元件通常具有非線性特性,需要考慮元件的微觀行為和相互作用。例如,射頻放大器、功率放大器和高速數(shù)字電路等。
小信號等效電路主要應用于低頻、低功率和線性電路的分析和設計。這些電路中的元件通常具有線性特性,可以通過線性化的方法來簡化電路的分析。例如,音頻放大器、濾波器和傳感器電路等。
- 分析方法
微變等效電路的分析方法主要包括:
(1)元件建模:根據(jù)電路中各個元件的物理特性和行為,建立相應的數(shù)學模型,如電容、電感、電阻、二極管、晶體管等。
(2)電路拓撲分析:根據(jù)電路的拓撲結(jié)構,確定電路中各個元件之間的連接關系和相互作用。
(3)電路方程求解:根據(jù)電路中的元件模型和拓撲結(jié)構,建立電路的微分方程或代數(shù)方程,并通過數(shù)值或解析方法求解電路的性能參數(shù)。
小信號等效電路的分析方法主要包括:
(1)線性化處理:將電路中的非線性元件進行線性化處理,如通過泰勒級數(shù)展開等方法,將非線性元件轉(zhuǎn)化為線性元件。
(2)等效電路構建:根據(jù)電路中的線性元件,構建等效電路,如電阻、電容、電感等。
(3)電路分析:通過等效電路,使用線性電路分析方法(如節(jié)點電壓法、回路電流法等)來求解電路的性能參數(shù)。
- 優(yōu)缺點
微變等效電路的優(yōu)點:
(1)能夠準確描述電路中各個元件的微觀行為和相互作用,適用于高頻、高速和大功率電路的分析和設計。
(2)可以提供豐富的電路性能參數(shù),如增益、帶寬、失真、穩(wěn)定性等。
(3)可以用于電路的優(yōu)化設計,提高電路的性能和可靠性。
微變等效電路的缺點:
(1)分析過程較為復雜,需要考慮電路中各個元件的物理特性和行為,計算量較大。
(2)對于非線性元件的建模和分析,需要較高的專業(yè)知識和技能。
小信號等效電路的優(yōu)點:
(1)分析過程相對簡單,適用于低頻、低功率和線性電路的分析和設計。
(2)可以通過線性化處理,簡化電路的分析,降低計算量。
(3)可以快速獲得電路的性能參數(shù),如增益、帶寬、失真等。
小信號等效電路的缺點:
(1)對于非線性元件,需要進行線性化處理,可能存在一定的誤差。
(2)對于高頻、高速和大功率電路,可能無法準確描述電路的性能。
- 結(jié)論
微變等效電路和小信號等效電路是電子電路分析中兩種重要的等效電路方法。它們在電路設計和分析中有著廣泛的應用。微變等效電路適用于高頻、高速和大功率電路的分析和設計,可以準確描述電路中各個元件的微觀行為和相互作用;而小信號等效電路適用于低頻、低功率和線性電路的分析和設計,可以通過線性化處理,簡化電路的分析。
-
功率放大器
+關注
關注
102文章
3927瀏覽量
133823 -
元件
+關注
關注
4文章
1065瀏覽量
37440 -
電子電路
+關注
關注
78文章
1242瀏覽量
67676 -
微變等效電路
+關注
關注
5文章
14瀏覽量
6379
發(fā)布評論請先 登錄
諾頓等效電路和戴維南等效電路的區(qū)別
晶體管的微變等效電路相關資料分享
如何一秒學會畫微變等效電路?(等效電路畫圖技巧)
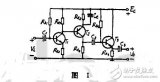
共射放大電路的微變等效電路分析詳情
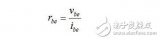
微變等效電路分析法解析
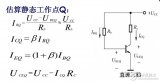





 微變等效電路和小信號等效電路的區(qū)別
微變等效電路和小信號等效電路的區(qū)別










評論