相噪是與哪種類型的抖動相對應？如何理解相位噪聲與時間抖動的關系？

相位噪聲與時間抖動是兩個在信號處理領域中經常涉及的概念。在討論相位噪聲時，我們常常聽到相位噪聲和時間抖動的聯系。因此，本文將探討相位噪聲和時間抖動的含義以及它們之間的關系。

一、時間抖動

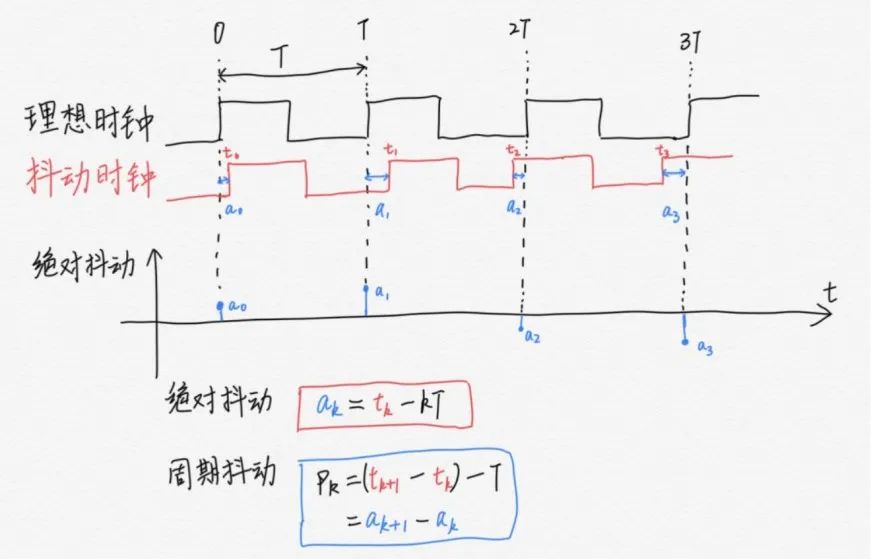
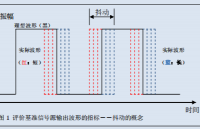
時間抖動是指信號的相位相對于一組參考信號的期望相位的偏差。它可以由以下數學公式表示：

$t_j = \frac{\phi_j}{2 \pi f_c}$

其中，$t_j$表示第$j$個采樣點的時間偏移；$\phi_j$是該采樣點的相位偏移；$f_c$是信號的中心頻率。時間抖動的單位為秒。

二、相位噪聲

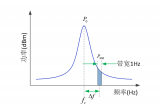
相位噪聲是指信號的相位在頻率上的偏移。它通常由相位噪聲密度（PSD）來表示，即單位頻率內相位噪聲的平均功率。相位噪聲的單位為弧度。

三、相噪

相噪是指在頻率域內，信號的相位偏移噪聲。相噪是相位噪聲的一種體現。相噪和時間抖動之間有一個很重要的關系：在某些情況下，它們可以互相轉換。

四、理解相位噪聲和時間抖動的關系

相位噪聲和時間抖動是兩個不同的概念，但它們之間是有聯系的。具體來說，相位噪聲和時間抖動之間的關系可以通過以下公式表示：

$\Delta t_j = \frac{\Delta \phi_j}{2 \pi f_c \frac{\partial \phi}{\partial f}}$

其中，$\Delta t_j$是第$j$個采樣點的時間偏移誤差；$\Delta \phi_j$是該采樣點的相位偏移誤差；$\frac{\partial \phi}{\partial f}$是信號的相位斜率。

通過這個公式，我們可以看到，當信號的相位斜率越大時，時間抖動誤差越小。相反，當相位斜率越小時，時間抖動誤差越大。此外，如果相位噪聲密度相同，但是信號的中心頻率不同，那么時間抖動誤差也會有所不同。

總之，相位噪聲和時間抖動都是信號處理中非常重要的概念。相位噪聲是指信號的相位在頻率上的偏移，而時間抖動是指信號的相位相對于一組參考信號的期望相位的偏差。相噪是相位噪聲在頻率域內的體現，相位噪聲和時間抖動之間有一個很重要的關系：在某些情況下，它們可以互相轉換。通過深入理解這些概念之間的關系，我們可以更好地理解信號處理的內在機制，從而更好地應用它們來解決實際問題。