本文將繼續研究電壓模式Buck,從頻域邊帶效應和多頻率模型的角度,深度揭秘:
- PWM調制器在小信號環路中,究竟是何等效模型?在中高頻段,小信號的精確模型與傳統平均模型的偏差何在?
- 在中高頻段,精確的小信號模型與真實PWM變換器的系統是否仍有偏差?
LTI系統頻率響應的適用性
頻率響應,即穩態下線性時不變(LTI)系統的幅值/相位隨頻率的變化。它反映了任意頻率下,系統正弦輸出和對應正弦輸入的一一對應關系,且LTI系統的輸出響應和輸入信號的注入時刻無關。
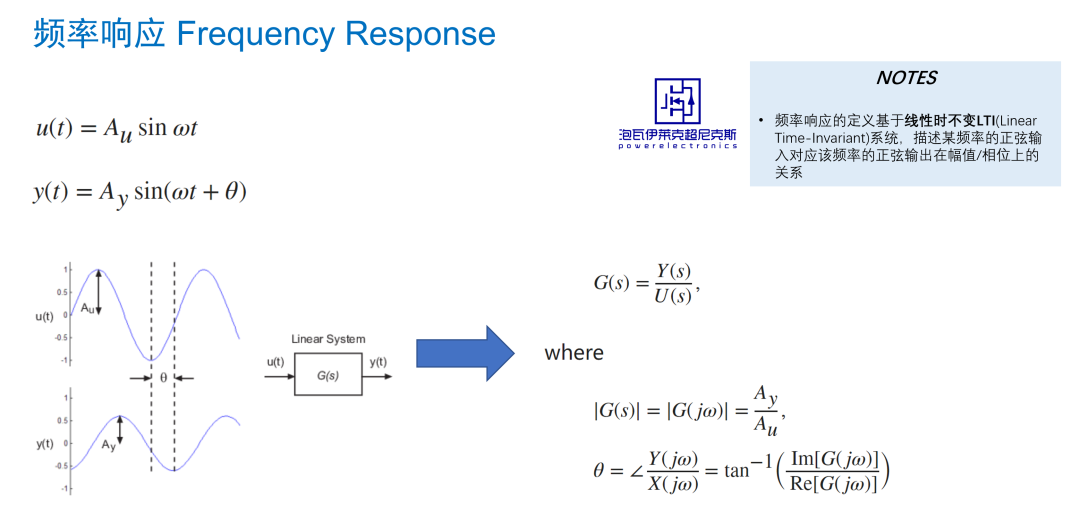
LTI系統頻率響應的定義
然而,前文提過PWM調制器具有時變的采樣特性,時變系統本身已經破壞了LTI系統的分析基礎。若從頻域上考察PWM變換器,在閉環回路中注入一個接近fsw的高頻擾動 fx ,可以明顯看到Buck的輸出電壓* vo存在一個 ** fsw -fx的差頻響應(beat frequency),這是由于fx經過開關頻率fs的載波自然采樣下的邊帶效應造成的。如此,系統在某頻率下的輸出響應并不僅僅由該頻率的擾動輸入貢獻,這是LTI系統頻率響應無法描述*的特性。

非LTI系統中頻率響應不再適用
PWM變換器的時變特性,導致越往高頻處越遠離一個LTI系統,在LTI波特圖理論下的頻響指標(帶寬/穩定裕量等)參考價值越低。有學者提出利用線性周期LTVP/LTP系統理論建模和分析,這是足夠嚴謹的,但分析手段在數學上過于復雜且物理意義并不直觀。
小信號精確模型的意義
在介紹系統大小信號建模時,已簡單歸納過小信號建模的部分手法,本文將中高頻小信號精確建模的途徑重新歸納如下。

小信號精確建模的方法分類
PWM調制器在中高頻的時變特性已然不可忽略,勢必造成使用LTI系統理論下的小信號模型,即便是環路分析儀直接掃頻的結果,也無法精準描述實際PWM變換器的全部特性(下圖可形象說明這個問題)。但是,從理論上建立小信號精確模型仍然是有必要的,因為 頻率響應和波特圖分析方法是工程實踐普遍接受的設計習慣 ,精確建模可在中高頻無限接近實際的環路掃頻結果,從而給基于頻率響應的 環路補償和高帶寬設計提供理論指導 ,同時也可從小信號頻域的角度大致預測中高頻的不穩定行為(如次諧波振蕩)。另一方面,基于平均模型的建模思路不斷改進而來的頻域精確建模方法,最容易被工程實踐人員理解和使用。

各數學模型的關系
既然通過頻域波特圖設計環路依然是工程實踐的絕對主流,本文將從頻域的角度介紹邊帶效應和多頻率小信號精確模型,以幫助大家理解PWM調制器在中高頻究竟帶來了什么。
邊帶效應和頻率混疊/耦合
下圖通過例子說明了開環的PWM調制器,自然采樣下的時變特性:占空比的輸出響應和輸入調制波的注入時刻相關。

PWM調制器自然采樣的時變特性
開環情況下,如果把PWM調制器看做fsw的采樣環節,調制波在某頻率的小信號擾動輸入下,會在頻域以nfsw為中心,產生周期性的延拓,這些因fsw采樣產生的高頻信號稱為 **nfsw **的 邊帶效應 。


PWM調制器的邊帶效應與頻率混疊
然而,閉環中的PWM調制器比僅考慮開環PWM調制器的特性更為復雜。環路是一個低通濾波器,調制波的擾動產生的邊帶會在閉環繞一圈后重新回到調制器參與調制,導致PWM占空比輸出的響應既含有擾動頻率成分,又含有各邊帶頻率成分, 擾動頻率和邊帶頻率相互耦合 (有文獻也稱這種耦合是PWM調制器的頻率混疊,這取決于頻率混疊如何明確定義)。


PWM調制器的邊帶效應在考慮閉環以后的頻率耦合
由上圖容易知道:擾動頻率越高,越接近 nfsw * ,則越容易在低頻處產生差頻的輸出響應; 且環路的帶寬設計得越高,更多落在低頻的邊帶成分將被有效放大,邊帶效應造成的頻率耦合越嚴重 ,傳統的小信號平均模型造成的誤差是非常顯著的。

頻率越高,越不可忽略邊帶效應和閉環的頻率耦合
多頻率模型
逐步考慮高頻和大紋波
基于頻域邊帶的小信號精確建模被稱為“多頻率模型”,始于CPES邱陽在2005年左右的研究,考慮采樣帶來的高頻邊帶效應以及在閉環系統中的頻率耦合。

多頻率模型的發展
近年來,眾多學者對邱陽多頻率模型的精度不斷優化,考慮的邊帶數越來越多,配合對大幅度調制紋波具體形狀的分析,可以突破“低頻假設”和“小紋波假設”的雙重限制,求得和環路分析儀擾動法掃頻幾乎一致的結果。

不同多頻率模型考慮的邊帶數
在調制波幅值和載波相比不可忽略的情況下,調制波含“大紋波”對小信號全頻段增益和中高頻段相位帶來的影響也是顯著的。學術界從引入紋波的開關頻率正弦基波開始,結合多頻率模型共同分析。

調制波是“大紋波”情況下對小信號模型的影響
為了同時解決所有高頻邊帶和所有紋波頻率分量對小信號的影響,本文引用南航李鑫博士的“拓展頻率模型”及其結論說明PWM調制器在小信號模型中的特性。
拓展頻率模型
完整的PWM調制器小信號模型
在已知補償器參數進而考慮“大紋波”形狀的PWM調制下,結合邊帶效應和閉環頻率耦合,可得到一個完整的PWM調制器小信號模型。下圖給出的是PI補償器的閉環Buck,其PWM調制器的小信號傳遞函數GPWM的近似結果。


PI補償的閉環Buck,完整的PWM調制器小信號模型GPWM
由下圖的例子可以明顯看到:
- GPWM不再是平均模型中的恒定增益,而是和紋波形狀(補償器參數、主電路參數、開關頻率、占空比共同決定)相關
- GPWM近似為一階系統,在平均模型1/Vm基礎上多了一個增益調節量和一個極點,它們均和補償器的Kp相關(一個正相關,一個反相關)
- 試圖提高帶寬的過程中,增大補償器Kp往往會增大全頻增益,但會降低中高頻的相位,無法保證充足的相位裕量
- 有兩點可能性是相當反直覺的,因GPWM的增益調節量和極點均可正可負:
①有時,增大補償器Kp反而有可能降低 GPWM的增益 ,導致環路增益和帶寬不再提升
** ②有時, 極點也有可能成為右半平面的開環不穩定極點**

GPWM和小信號環路隨增益Kp的變化趨勢
兩個反直覺的實例
嘗試把帶寬提升到逼近fsw/2
綜上所述,我們將PWM調制器的特點總結如下。

用邊帶效應理解PWM調制器的總結
當我們試圖通過增大補償器Kp,盡可能地提升帶寬直至逼近 fsw /2的過程中,不難遇到上述兩點反直覺的可能性,即增大補償器Kp對環路增益/帶寬的提升無效,和產生中高頻的右半平面極點。如下的仿真實例可以印證。


必須再次強調,正如本文一開始所談的那樣,從結果上看,帶寬可以提高直到逼近 fsw /2系統仍是穩定的,但此時依然是基于LTI系統理論的分析手段,波特圖上的帶寬和相位裕量等指標已經部分失去了參考價值。 這也是設計經驗提示我們要把小信號環路的帶寬設計在開關頻率1/10-1/5范圍內的深層原因 。
-
PWM
+關注
關注
116文章
5364瀏覽量
217943 -
變換器
+關注
關注
17文章
2130瀏覽量
110372 -
頻率響應
+關注
關注
1文章
103瀏覽量
18539 -
PWM控制
+關注
關注
7文章
195瀏覽量
26969 -
調制器
+關注
關注
3文章
889瀏覽量
46007 -
補償器
+關注
關注
0文章
87瀏覽量
14419
發布評論請先 登錄
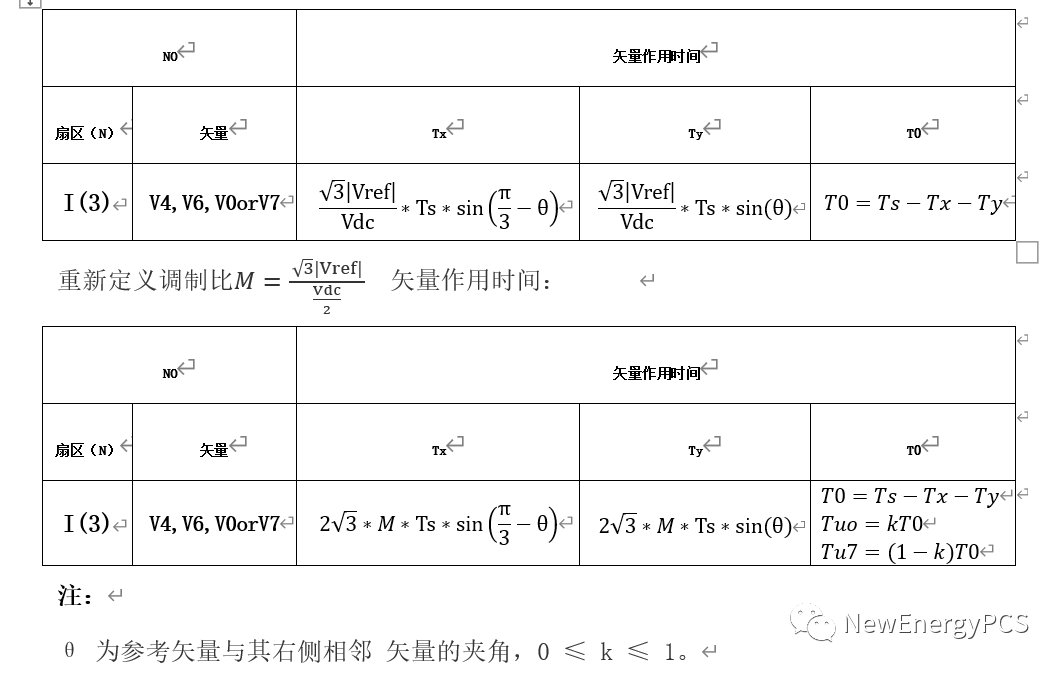
SVPWM調制波的數學表達究竟是怎樣的呢?





 PWM調制器在小信號環路中,究竟是何等效模型?
PWM調制器在小信號環路中,究竟是何等效模型?











評論