文章詳細(xì)對(duì)高斯濾波器的綜合設(shè)計(jì)進(jìn)行講解,解釋如何從時(shí)域無過沖推導(dǎo)出高斯濾波器的。并且深入探討了高斯濾波器的零極點(diǎn)分布。最后介紹基于Matlab的濾波器設(shè)計(jì)軟件,以低通、帶通濾波器為例,展示其功能,并給出Github相關(guān)鏈接。
高斯濾波器特點(diǎn)和用途
高斯濾波器(Gaussian Filter)濾波器是具有最佳時(shí)域特性的濾波器,其幅頻曲線具有高斯函數(shù)(Gaussian function)曲線分布特性,對(duì)階躍響應(yīng)無任何過沖,實(shí)際應(yīng)用中高斯逼近濾波器和貝塞爾逼近濾波器特性非常類似,隨著兩者階數(shù)增加兩者表現(xiàn)將趨于一致,高斯濾波器的能夠高保真的傳輸時(shí)域信號(hào)特點(diǎn)使得它在時(shí)域應(yīng)用中很重要,比如示波器設(shè)備,雷達(dá)設(shè)備等。當(dāng)然現(xiàn)在在數(shù)字圖像處理中應(yīng)用也非常廣泛。
高斯濾波器逼近
約束
- 1,是階多項(xiàng)式(可實(shí)現(xiàn)性,在頻率增益為0)
- 2,(低通定義,在頻率為0的位置增益為1)
- 3,(定義低通半帶寬)
- 4, 給定一個(gè)階躍信號(hào), 無過沖
- 5, 給定一個(gè)階躍信號(hào), 有最快上升沿(按階躍信號(hào)導(dǎo)數(shù)所生成的鐘形曲線的半寬度最小定義)
傅里葉變換
首先我們需要復(fù)習(xí)下連續(xù)時(shí)間傅里葉變換:
如下左圖是一個(gè)脈沖信號(hào),右圖是這個(gè)脈沖信號(hào)的連續(xù)傅里葉變換結(jié)果。
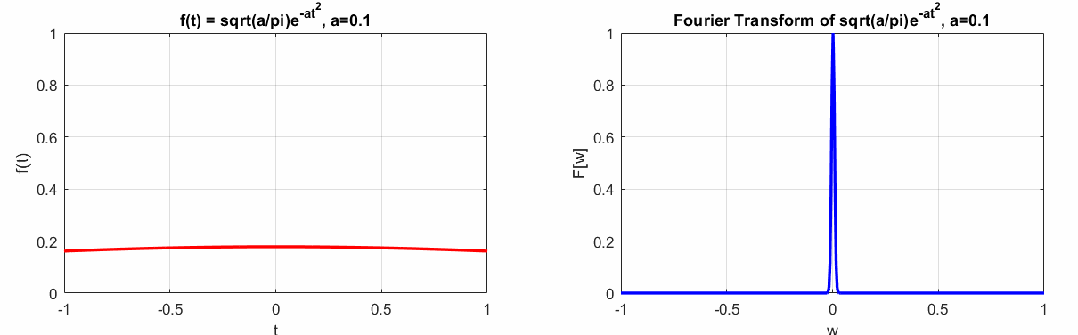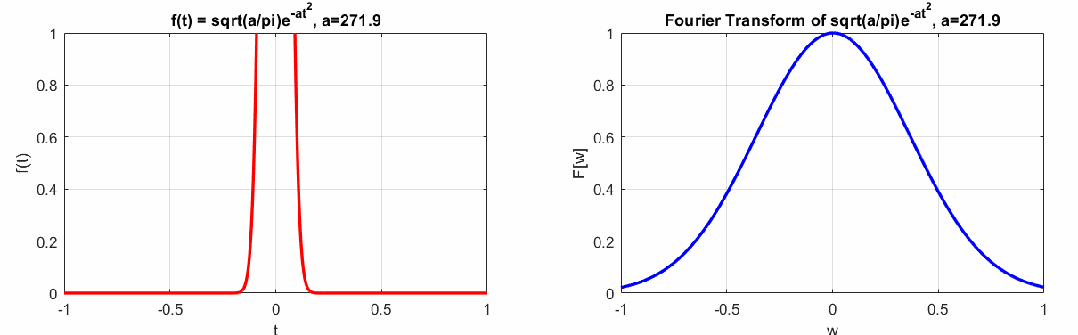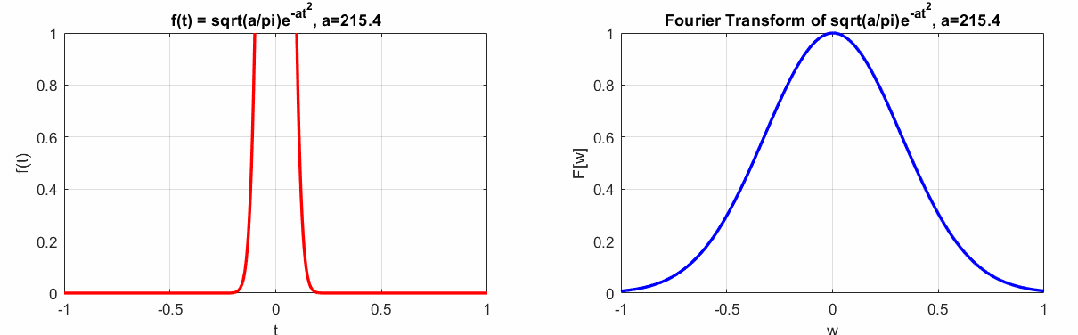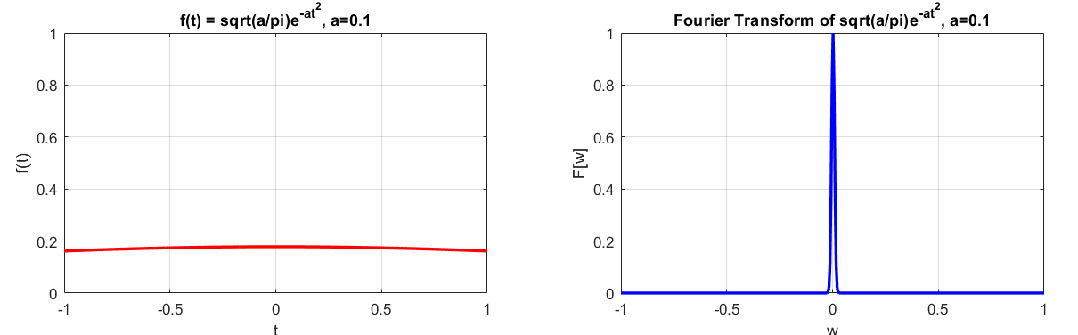
可以看到左邊曲線和右邊曲線的胖瘦關(guān)系相反,若左邊時(shí)域脈沖信號(hào)越瘦,右邊越胖,反之左邊越胖,右邊越瘦,這個(gè)特點(diǎn)即時(shí)間-頻域的不確定性原理(類似海森堡動(dòng)量-位置的不確定性原理),即時(shí)頻特性不能兼得(感興趣的同學(xué)可以參考時(shí)頻分析的相關(guān)書籍)。
時(shí)域階躍到頻響
從約束4可以看到一個(gè)階躍信號(hào)無過沖,這是一個(gè)時(shí)域信號(hào),而最后我們要求解的頻域響應(yīng),所以這里必然要用到時(shí)域-頻域轉(zhuǎn)換,即前面提到的傅里葉變換,以下是一個(gè)階躍信號(hào)如何變換為一個(gè)頻域響應(yīng)的:
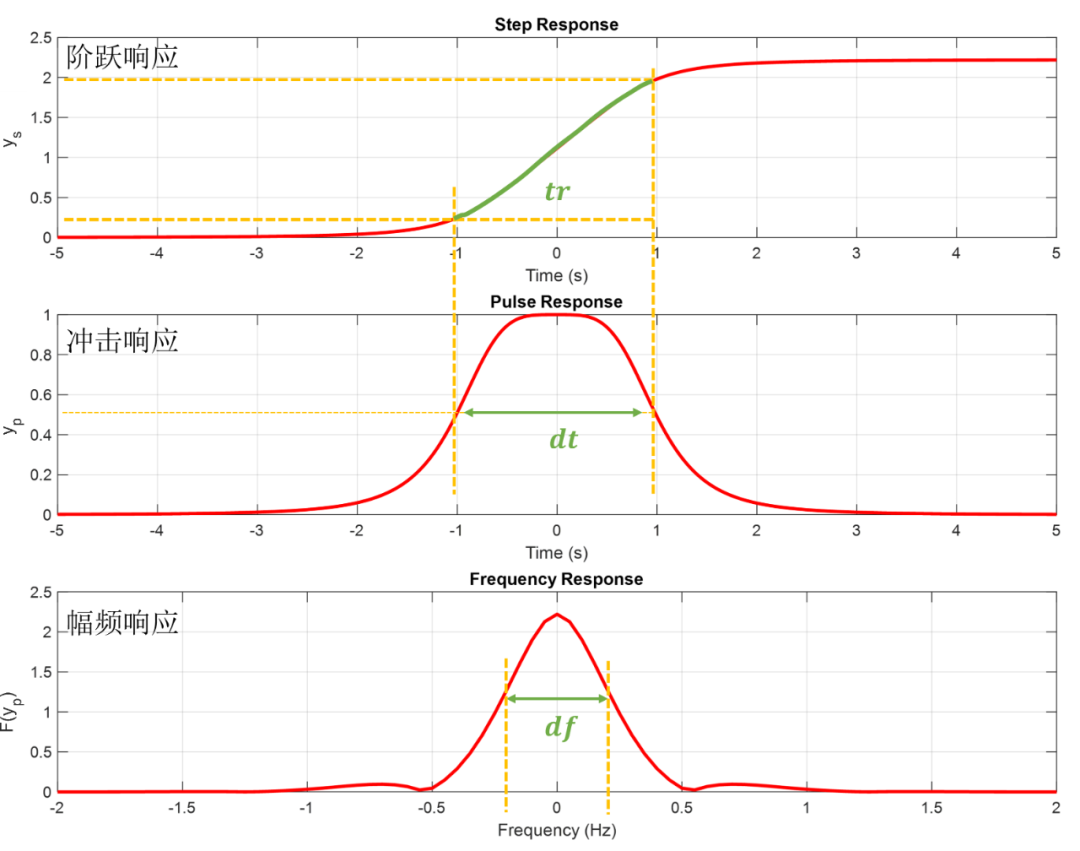
首先我們要對(duì)階躍響應(yīng)進(jìn)行微分,即可得到?jīng)_擊響應(yīng),然后運(yùn)用連續(xù)傅里葉變換(式1)將沖擊響應(yīng)轉(zhuǎn)換到頻域,即可得到頻響。
這里有一個(gè)重要的點(diǎn)是,階躍響應(yīng)的上升時(shí)間的計(jì)算,如圖中的階躍信號(hào)所展示的,表示上升時(shí)間,所對(duì)應(yīng)了沖擊響應(yīng)的脈沖寬度,這里的時(shí)域脈沖寬度選擇了脈沖的半時(shí)間寬度。而幅頻響應(yīng)的頻域?qū)挾却砹诉@個(gè)脈沖系統(tǒng)響應(yīng)的帶寬,這里的頻域脈沖寬度選擇了脈沖的半頻域?qū)挾?即-6dB截止頻率點(diǎn))。
有了上述鋪墊,我們可以求解出一個(gè)無過沖的最佳時(shí)頻濾波器了,從上面約束可以得到,當(dāng)頻域?qū)挾纫欢ㄇ闆r下,我們希望得到的階躍響應(yīng)無過沖,并且上升時(shí)間(即沖擊響應(yīng)寬度)最小的系統(tǒng)函數(shù),那么滿足這樣的系統(tǒng)函數(shù)是什么呢?
這要求,Gabor給出了答案(有關(guān)這個(gè)問題的討論可以參考),滿足這個(gè)時(shí)頻最佳響應(yīng)的濾波器即高斯濾波器(Gaussian Filter),即系統(tǒng)函數(shù)是:
換句話說:在給定的帶寬下,其階躍響應(yīng)上升時(shí)間最短且無過沖的濾波器就是高斯濾波器。
注意這里的帶寬和上升時(shí)間的定義與通常定義的不同。
高斯濾波器
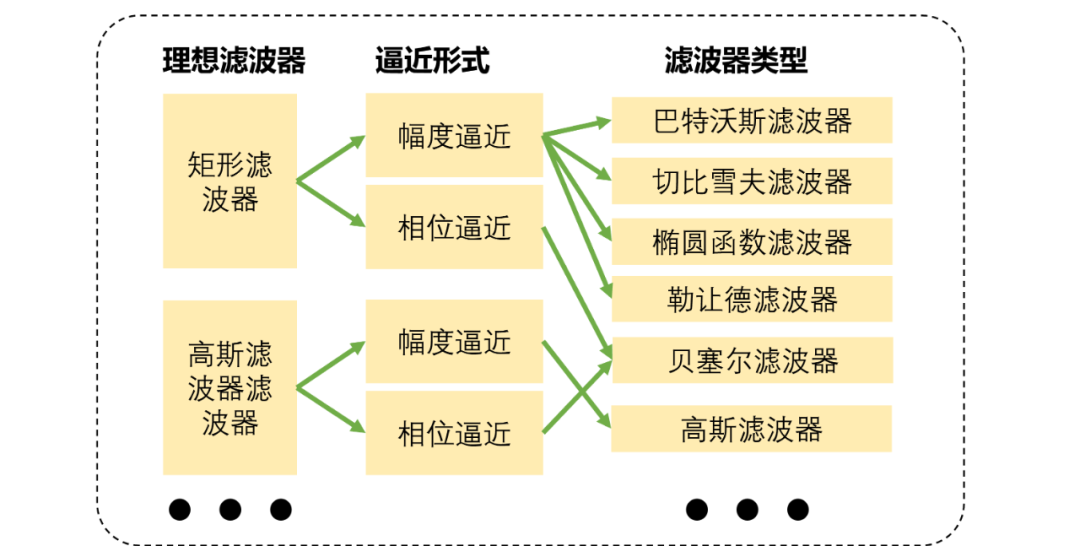
高斯濾波器是一類特殊的理想濾波器,其地位和矩形濾波器(Rectangular Filter, 也叫理想濾波器, Ideal Filter, 磚墻濾波器, Brick-wall Filter, sinc濾波器)相當(dāng),是無法通過多項(xiàng)式直接擬合得到的,只能通過函數(shù)逼近的方式得到,現(xiàn)在我們總結(jié)下現(xiàn)有濾波器設(shè)計(jì)。
總共有兩類濾波器綜合如下(當(dāng)然這個(gè)圖還可以擴(kuò)展):
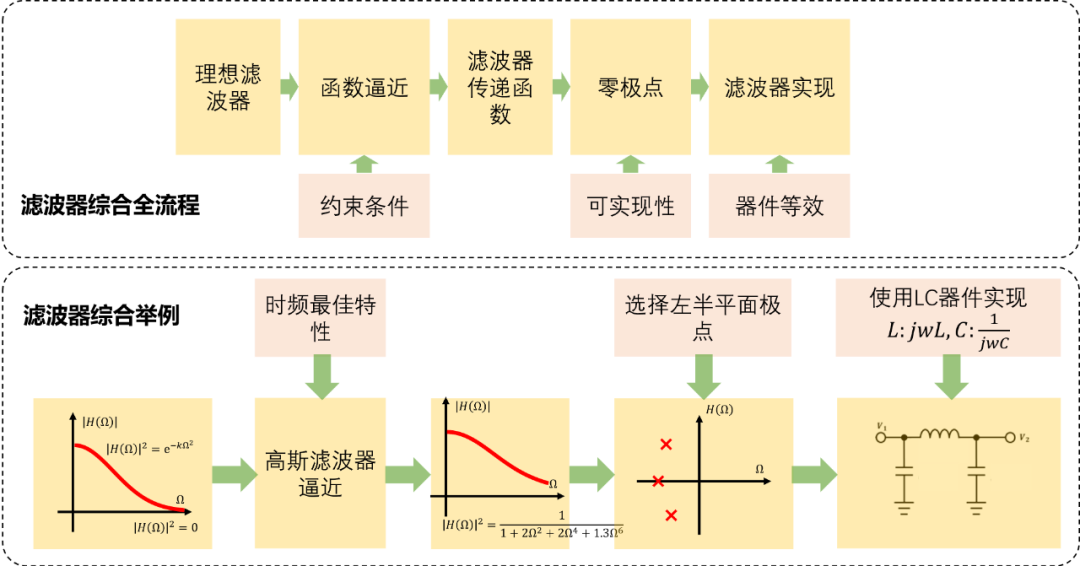
高斯濾波器綜合全流程如下:
高斯濾波器逼近
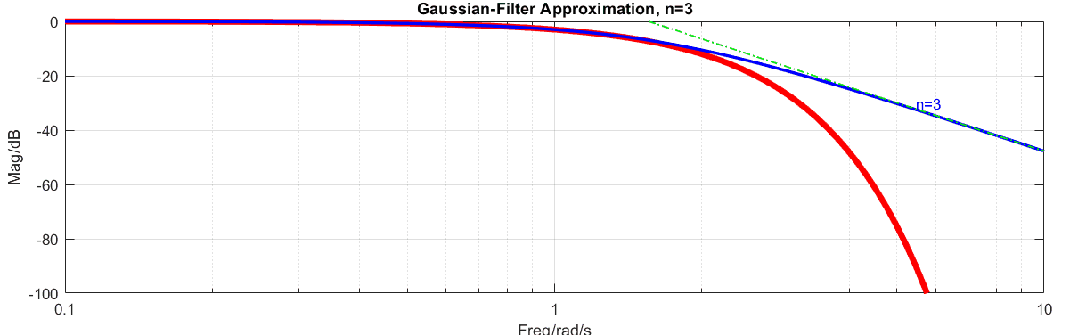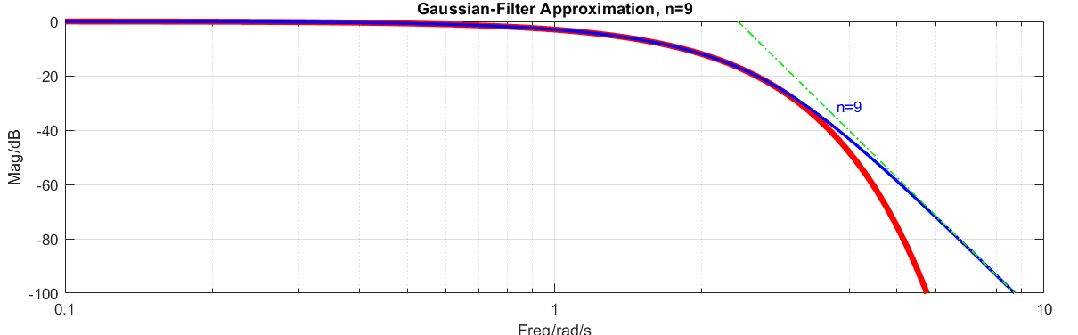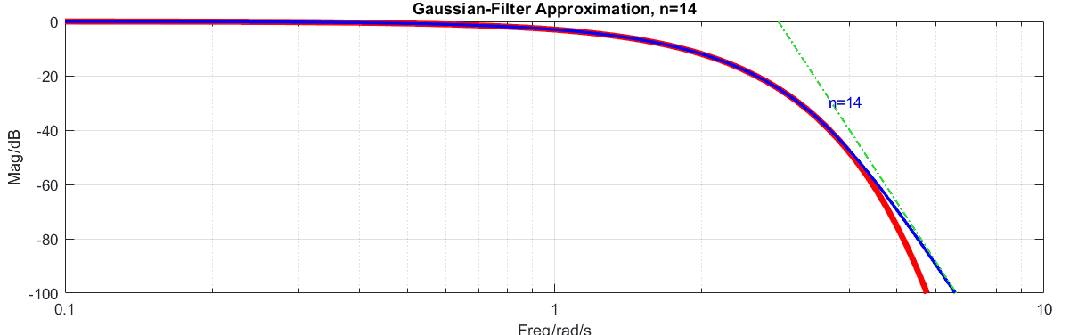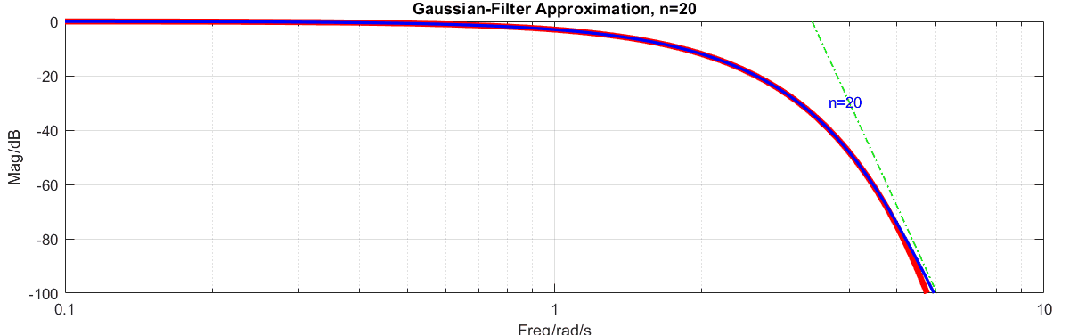
高斯濾波器是理想濾波器,其原因可以用如下動(dòng)圖說明,圖中高斯濾波器曲線是紅色曲線(式2),在對(duì)數(shù)-對(duì)數(shù)坐標(biāo)系下這樣高斯濾波器就是指數(shù)函數(shù),而藍(lán)色曲線是有理多項(xiàng)式逼近,在對(duì)數(shù)-對(duì)數(shù)坐標(biāo)系下,高頻范圍是線性的。使用一個(gè)線性函數(shù)去逼近指數(shù)函數(shù)顯然是不能完成的,所以無法使用有限階的有理多項(xiàng)式來逼近高斯函數(shù)。
我們只能使用多項(xiàng)式盡可能的去逼近高斯濾波器,這里常用的方法是泰勒展開,公式如下:
當(dāng)我們系統(tǒng)中要求頻率在時(shí)為其截止點(diǎn)時(shí):
令得到前7階高斯濾波器系數(shù)為():
| 濾波器階數(shù) | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
在s平面取其左半邊極點(diǎn)得到前7階高斯濾波器系數(shù)為():
| 濾波器階數(shù) | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 |
前7階高斯數(shù)濾波器極點(diǎn)為():
| 濾波器階數(shù) | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 |
同Bessel濾波器一樣需要有高斯濾波器帶寬修正系數(shù):
| 濾波器階數(shù) | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|
| 極點(diǎn)修正系數(shù) |
注:手機(jī)黨可橫屏查看表格
高斯濾波器零極點(diǎn)
和貝塞爾濾波器極點(diǎn)符合反斯托克斯線類似,高斯濾波器極點(diǎn)分布符合某個(gè)曲線,這個(gè)曲線公式為:
其中是實(shí)軸,是虛軸,其來源于的泰勒展開部分展開式零點(diǎn)的漸進(jìn)線——Szeg?曲線,Szeg?曲線分布(注意下圖橫坐標(biāo)為虛軸,縱坐標(biāo)為實(shí)軸)如下,其極點(diǎn)分布在一個(gè)水滴型曲線上,具體公式是(注意:這個(gè)是個(gè)近似公式,當(dāng)越大,精確度越高):
上式也可以化為和的形式:
這個(gè)公式只能在趨于無窮大時(shí)才和實(shí)際零點(diǎn)重合,而且趨近速度很慢,這里對(duì)其進(jìn)行擬合得到一個(gè)新近似公式(若希望得到更高精度的逼近可以參考,關(guān)于指數(shù)函數(shù)泰勒級(jí)數(shù)求和零點(diǎn)分布問題也是一個(gè)研究熱點(diǎn)):
效果如下動(dòng)圖所示(其中New Fit:式8的曲線;藍(lán)色曲線:Szego曲線的式6a;黑色的圓圈是Szego曲線的式6b,綠色盤面即指數(shù)泰勒展開式零點(diǎn)分布區(qū)域,紅色點(diǎn)是不同n下的實(shí)際零點(diǎn)位置):
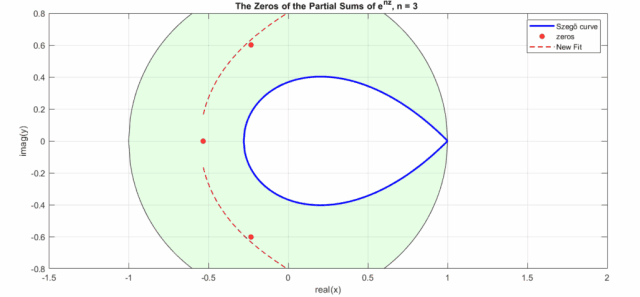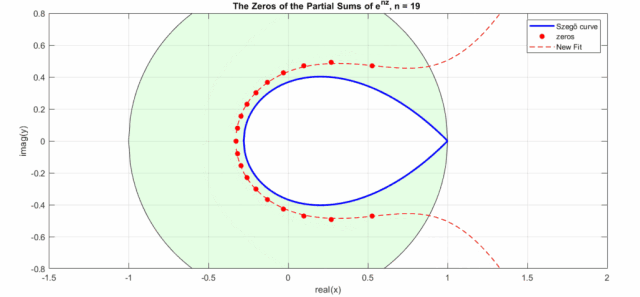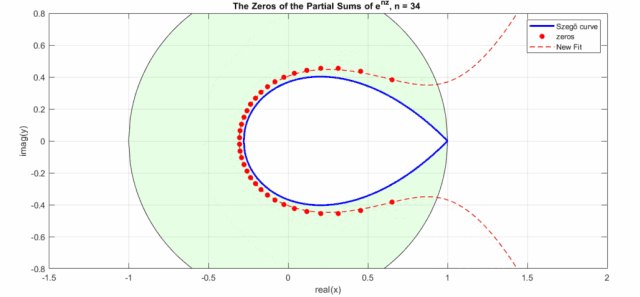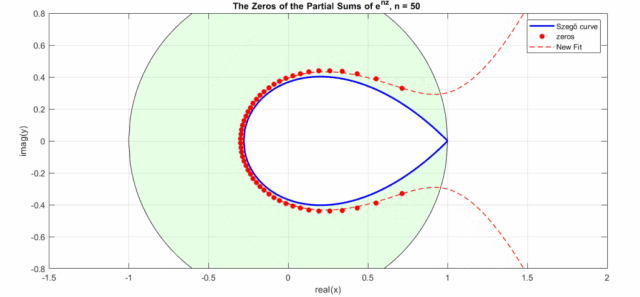
有了的零點(diǎn),那么高斯函數(shù)的零點(diǎn)也就可以簡(jiǎn)單的通過來求解,即:
令且那么得到:
通過這個(gè)變換后可以將指數(shù)函數(shù)的零點(diǎn)轉(zhuǎn)換為高斯函數(shù)的零點(diǎn):
上面的公式有所以,平方后將零點(diǎn)映射到虛軸(這里是軸)的右半部分。
按照轉(zhuǎn)換公式11,可以得到修正后的高斯函數(shù)零點(diǎn)為:
下圖是修正后的高斯函數(shù)(式12)零點(diǎn)曲線圖(注意,這里圖橫坐標(biāo)為虛軸,縱坐標(biāo)為實(shí)軸。藍(lán)色為Szego曲線式6經(jīng)過式11映射后的曲線,紅色虛線式式12表示的曲線,紅色點(diǎn)是高斯函數(shù)泰勒級(jí)數(shù)展開部分和的零點(diǎn)分布):
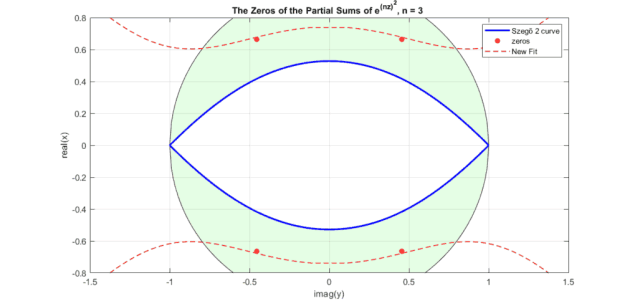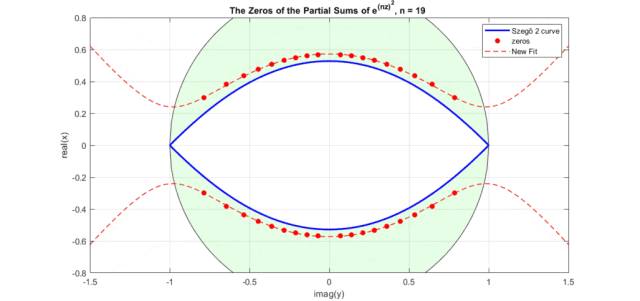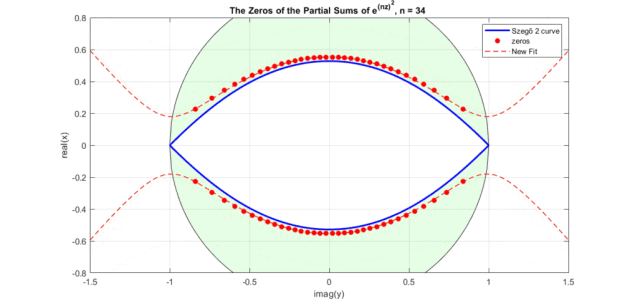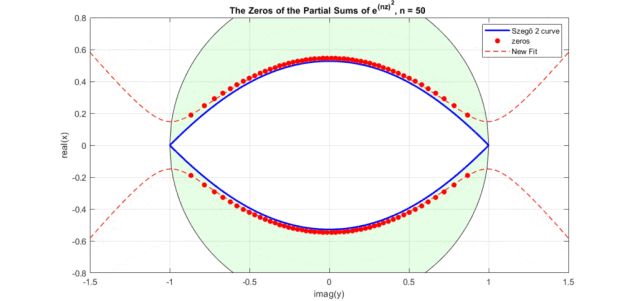
圖中出現(xiàn)了和Bessel多項(xiàng)式零點(diǎn)非常相似的圖形,是一個(gè)眼型曲線。
PS.通過平方,這個(gè)曲線變得更加對(duì)稱了,而且對(duì)稱點(diǎn)為原點(diǎn)。
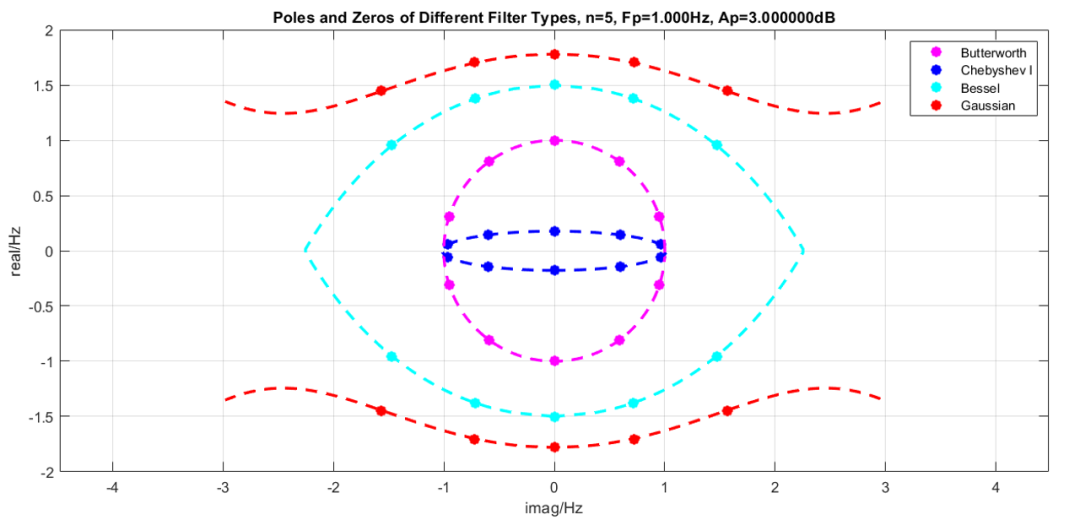
下面是四種不同濾波器極點(diǎn)的對(duì)比(以上討論是零點(diǎn),濾波器中由于求了個(gè)倒數(shù),故零點(diǎn)變極點(diǎn)),在這里我們得到了一只完整的眼睛。藍(lán)色曲線是切比雪夫I型濾波器極點(diǎn)分布,是瞳孔(Pupil);品紅色曲線是巴特沃斯濾波器極點(diǎn)分布,是眼球(Eyeball);青色曲線是貝塞爾濾波器極點(diǎn)分布,是眼瞼(Eyelash);紅色曲線是高斯濾波器極點(diǎn)分布,是眼皮(Eyelid)。
高斯濾波器的過沖
高斯濾波器在理想情況下無過沖,原因是高斯函數(shù)的逆傅里葉變換也是高斯函數(shù),也是時(shí)域的沖擊響應(yīng),高斯函數(shù)恒定大于0,即積分后無斜率小于0的點(diǎn),所以沒有過沖。但是使用泰勒展開高斯函數(shù)逼近后的濾波器卻是有過沖的,如下圖顯示了不同濾波器的過沖(縱坐標(biāo)改為對(duì)數(shù)用于不同濾波器的對(duì)比):
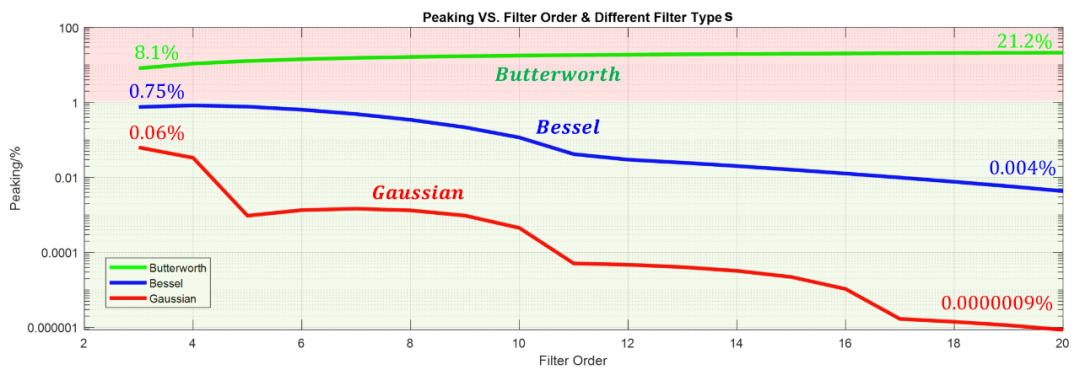
從中可以看到巴特沃斯濾波器的Peaking隨著階數(shù)增加而增加,但是貝塞爾和高斯濾波器隨著階數(shù)的增加Peaking是減小的!而且從趨勢(shì)看到,當(dāng)后,高斯濾波器和貝塞爾濾波器的過沖都會(huì)趨近于0。
高斯濾波器綜合
高斯濾波器綜合和巴特沃斯濾波器一樣,屬于全極點(diǎn)濾波器,所以這里僅僅列出一個(gè)3階高斯濾波器綜合實(shí)例,以供參考:
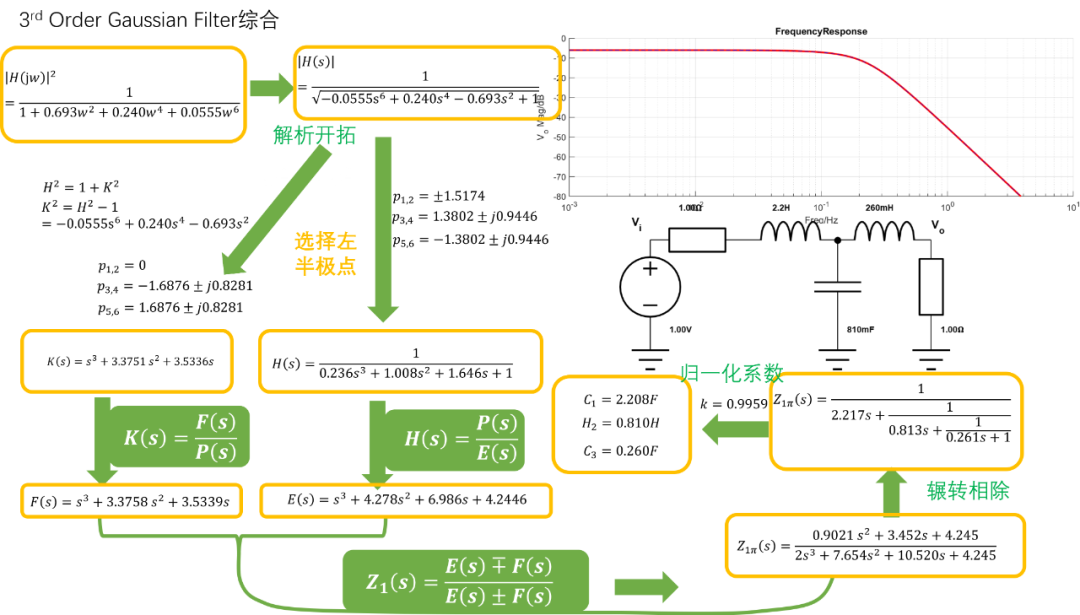
對(duì)于高斯濾波器,其綜合出來的電路器件值和貝塞爾濾波器器件值非常相似:
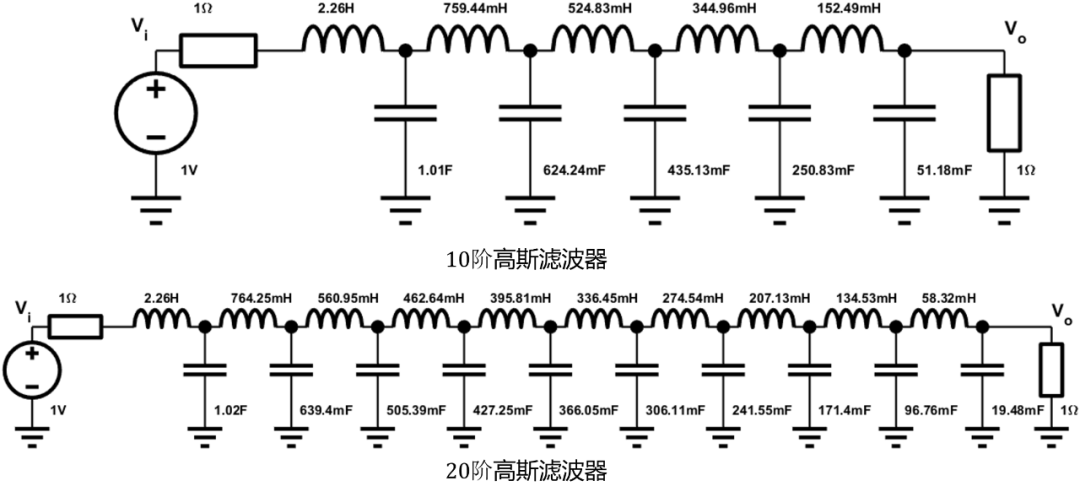
可以看到濾波器第一個(gè)器件值幾乎是相等的,而且距源越遠(yuǎn)器件值越小,下圖繪出了2-20階低通高斯濾波器系數(shù)圖,可以看出隨著階數(shù)的增加,前級(jí)器件值非常接近。
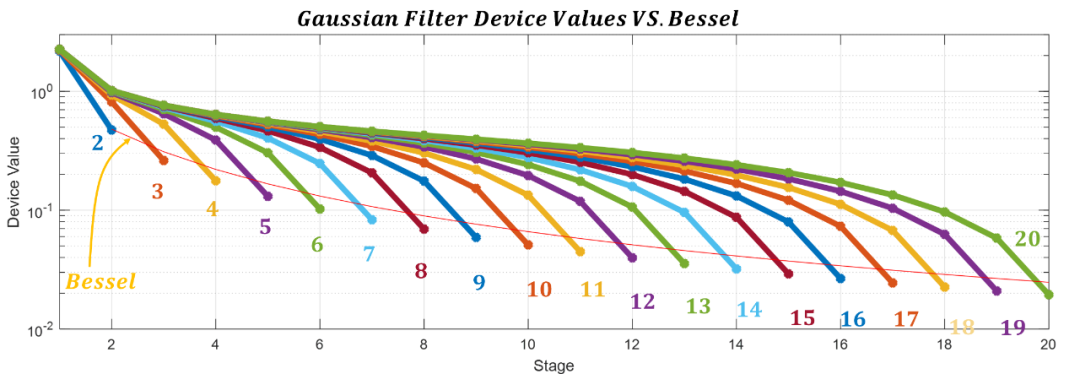
對(duì)比貝塞爾濾波器器件值而言,高斯濾波器器件值要小些。
任意負(fù)載條件下的高斯濾波器綜合
這里需要求解特征多項(xiàng)式,即需要求解(這里有關(guān)概念可以參考濾波器設(shè)計(jì)的逼近方法 - Butterworth, Chebyshev, Elliptic):
式中的定義參考模擬無源濾波器設(shè)計(jì)(六)-Chebyshev濾波器設(shè)計(jì)詳解中關(guān)于任意負(fù)載條件下的求解公式。
不同濾波器通帶類型之間的轉(zhuǎn)換
只要有了低通原型, 其他濾波器通帶類型之間的轉(zhuǎn)換同Butterworth濾波器模擬無源濾波器設(shè)計(jì)(五)-Butterworth濾波器設(shè)計(jì)詳解。
高斯濾波器設(shè)計(jì)軟件
基于Matlab的appdesign工具開發(fā)了一套濾波器設(shè)計(jì)軟件, 主要特點(diǎn)是:
- 支持高斯濾波器(Gaussian Filter)、貝塞爾濾波器(Bessel Filter)、橢圓函數(shù)濾波器(Elliptic/Cauer Filter)、切比雪夫?yàn)V波器(Chebyshev I)、逆切比雪夫?yàn)V波器(Chebyshev II, Inverse Chebyshev)、巴特沃斯濾波器(Butterworth)設(shè)計(jì)
- 支持4種不同濾波器通帶類型(LPF,HPF,BPF,BRF)設(shè)計(jì)
- T型和PI型結(jié)構(gòu)濾波器隨意切換
- 可以設(shè)置阻帶衰減決定濾波器階數(shù)
- 可以設(shè)置通帶衰減來綜合濾波器
- 可以隨意配置負(fù)載和終端阻抗, 并支持一端接載(源端電阻短路, 源端電流源, 終端開路, 終端短路)設(shè)計(jì)
- 可以幅頻響應(yīng)分析、零極點(diǎn)分析、瞬態(tài)分析
- 可以顯示理想頻率響應(yīng)、零極點(diǎn)和實(shí)際仿真的的頻率響應(yīng)、零極點(diǎn)
- 可以支持實(shí)際標(biāo)準(zhǔn)器件逼近設(shè)計(jì)
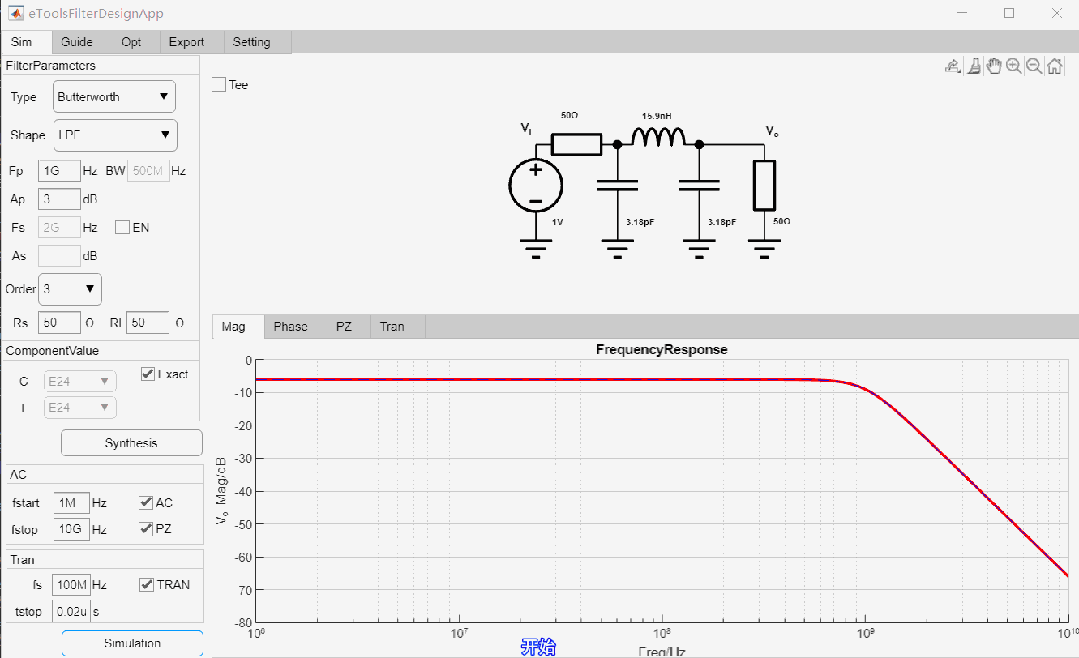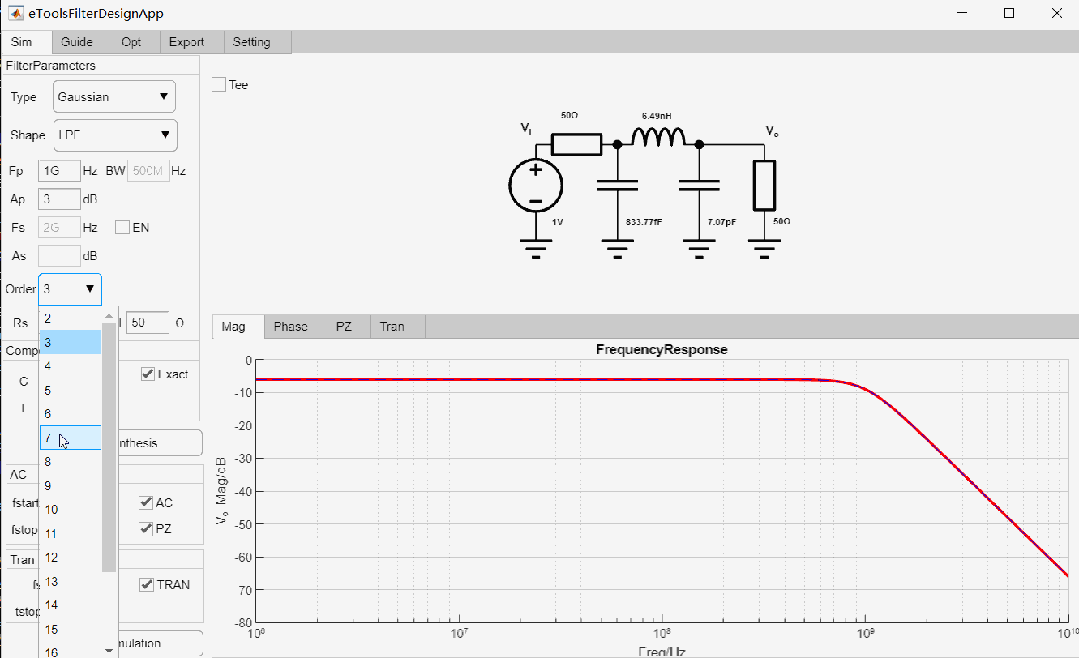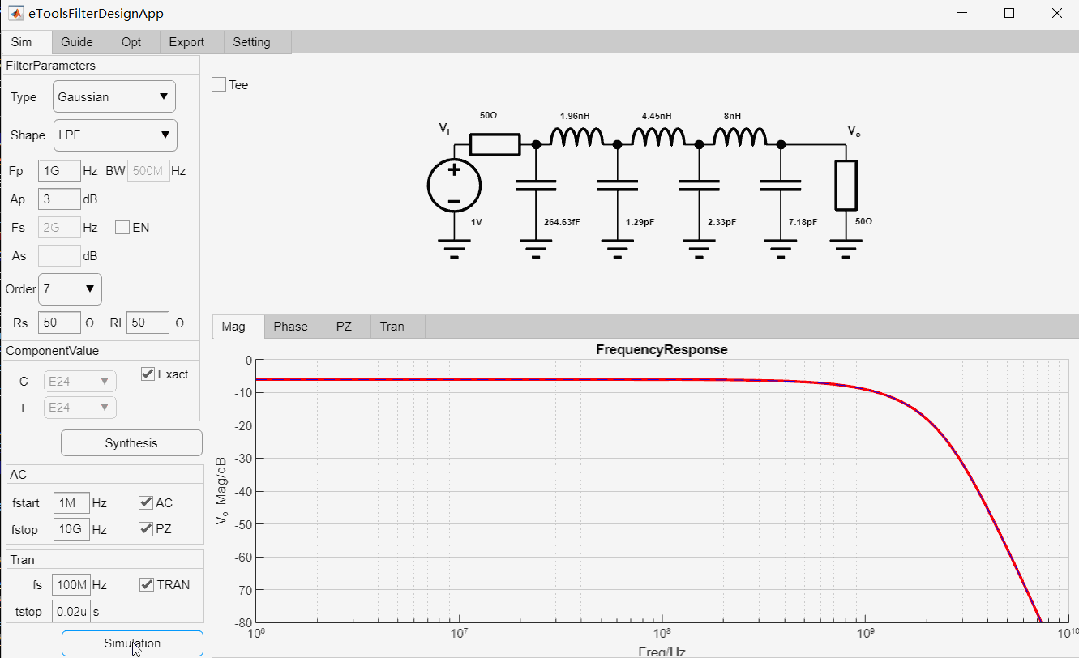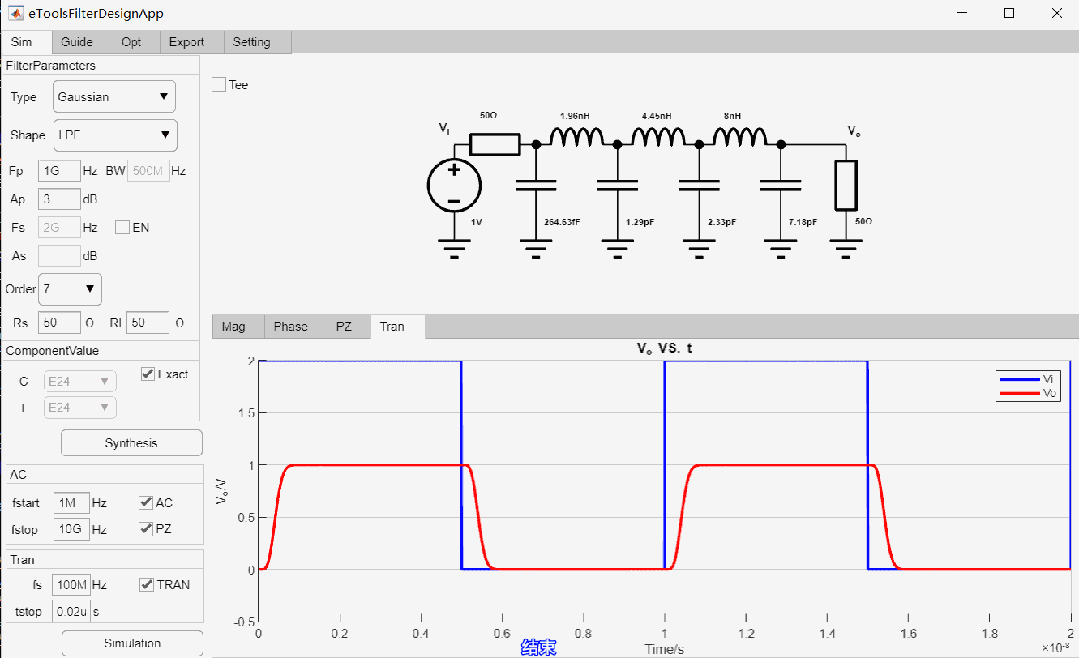
Gaussian LPF設(shè)計(jì)舉例
設(shè)計(jì)一款-3dB截止頻率為1GHz, 7階低通Gaussian濾波器,輸入輸出阻抗為50歐姆,設(shè)計(jì)過程如下:
最終設(shè)計(jì)參數(shù)如下:
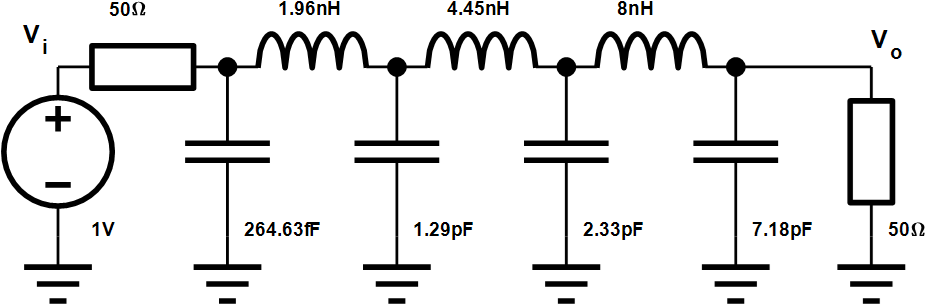
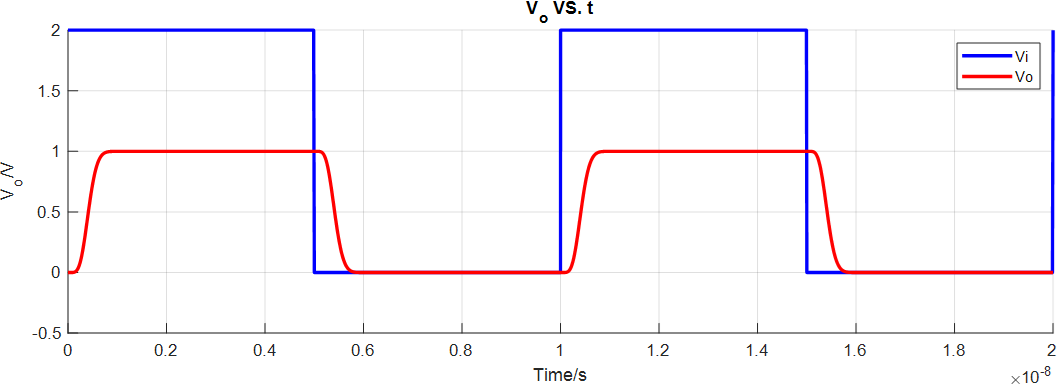
高斯濾波器瞬態(tài)仿真結(jié)果:
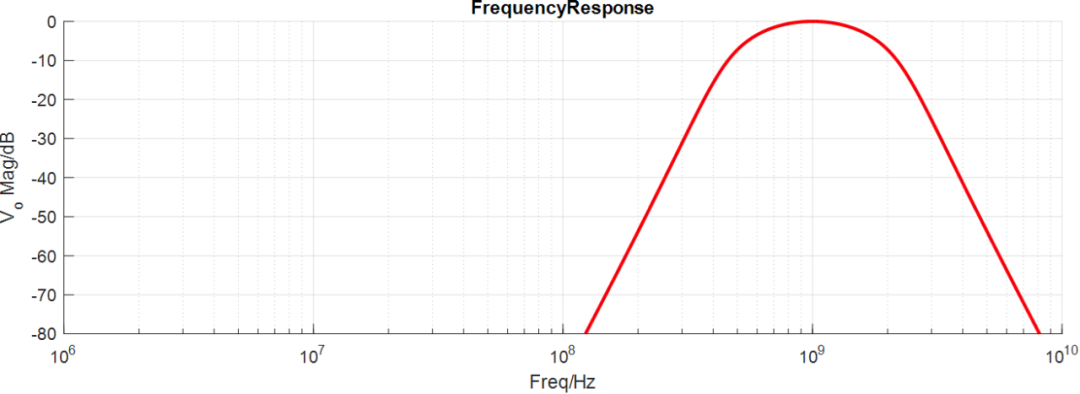
Gaussian BPF設(shè)計(jì)舉例
設(shè)計(jì)6階帶通Gaussian濾波器, 中心頻率為1GHz,帶寬為1GHz,50歐姆輸入,輸出阻抗為高阻,最后進(jìn)行瞬態(tài)仿真,設(shè)計(jì)過程如下:

最終設(shè)計(jì)參數(shù)如下:

AC仿真結(jié)果:
瞬態(tài)仿真結(jié)果:
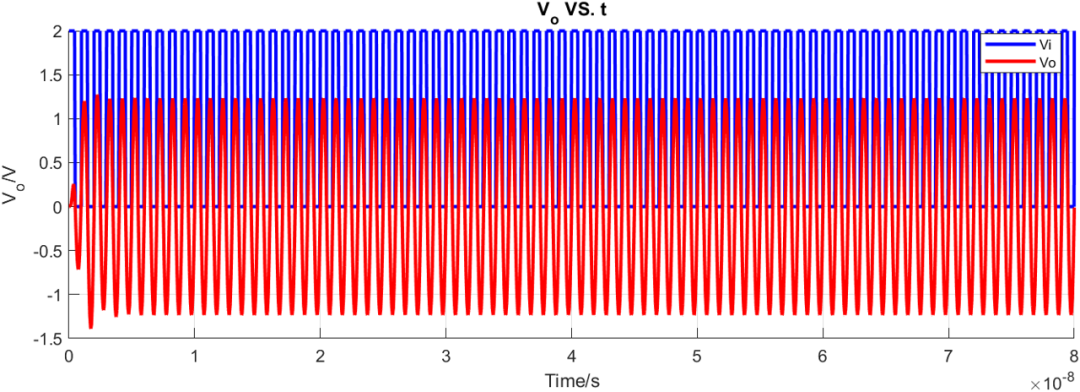
如果將濾波器帶寬繼續(xù)變窄為100MHz:
高斯濾波器的瞬態(tài)特性:
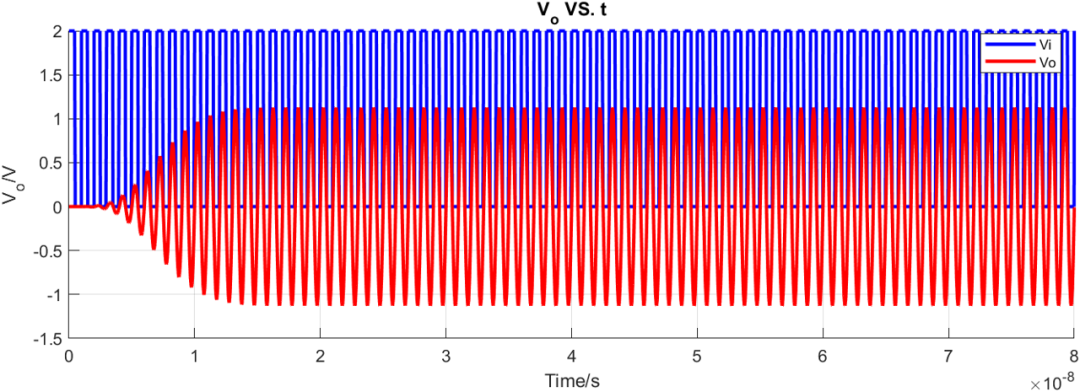
同樣參數(shù)對(duì)比貝塞爾濾波器的瞬態(tài)特性:
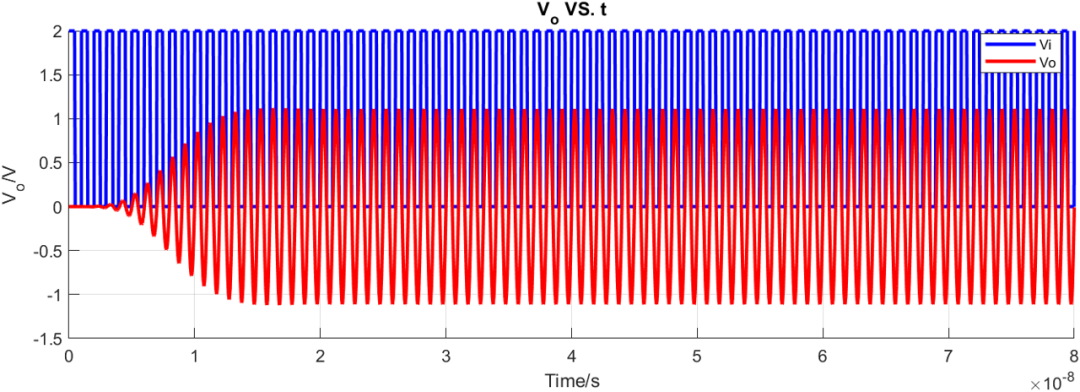
同樣參數(shù)對(duì)比巴特沃斯瞬態(tài)特性:
可以看到同樣濾波器設(shè)置參數(shù)下,高斯濾波器具有最小延遲和最小過沖。
程序的Matalb源碼已經(jīng)上傳GitHub中(https://github.com/etools361/MatlabGaussianFilterDesignApp),有興趣的同學(xué)可以下載試用體驗(yàn),當(dāng)然也歡迎技術(shù)交流。
-
示波器
+關(guān)注
關(guān)注
113文章
6527瀏覽量
188156 -
無源濾波器
+關(guān)注
關(guān)注
4文章
79瀏覽量
15424 -
GitHub
+關(guān)注
關(guān)注
3文章
481瀏覽量
17441
原文標(biāo)題:模擬無源濾波器設(shè)計(jì)(九)-Gaussian濾波器設(shè)計(jì)詳解
文章出處:【微信號(hào):電路設(shè)計(jì)小工具,微信公眾號(hào):電路設(shè)計(jì)小工具】歡迎添加關(guān)注!文章轉(zhuǎn)載請(qǐng)注明出處。
發(fā)布評(píng)論請(qǐng)先 登錄
有源濾波器和無源濾波器的區(qū)別?
轉(zhuǎn):有源濾波器和無源濾波器
模擬濾波器實(shí)驗(yàn)
無源帶通濾波器電路,有源帶通濾波器原理圖
無源濾波器的原理,和無源濾波器電路設(shè)計(jì)詳細(xì)解析





 模擬無源濾波器設(shè)計(jì)(九)-Gaussian濾波器設(shè)計(jì)詳解
模擬無源濾波器設(shè)計(jì)(九)-Gaussian濾波器設(shè)計(jì)詳解










評(píng)論