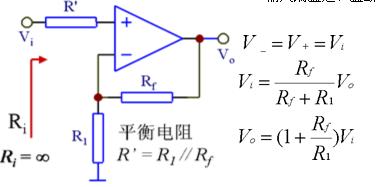
實際應用中,常要獲取兩個信號的差值或對多個模擬信號進行疊加混合,這時就要使用信號疊加電路和求差電路。圖一所示的反相比例和同相比例電路是比例運算電路的基本拓撲結構,以此為基礎,利用疊加原理和戴維南定理就可以構造出信號疊加電路和求差電路。
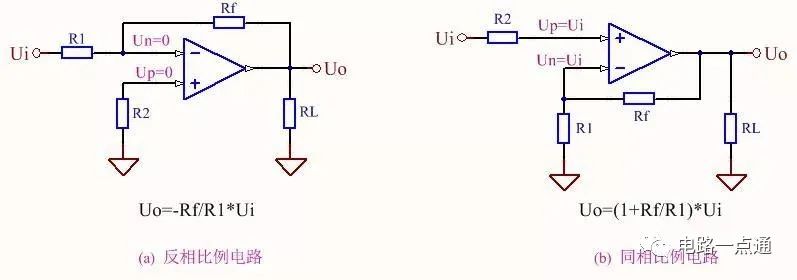
圖一 比例運算電路基本拓撲結構
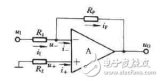
一. 信號疊加分同相疊加和反相疊加,圖二為信號同相疊加電路,其戴維南等效電路如圖二右側所示。
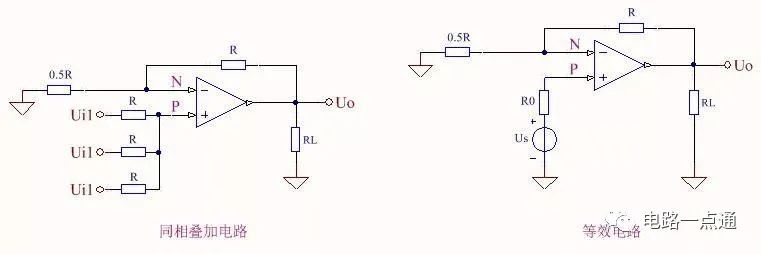
圖二 同相疊加及其等效電路
從圖二可看出,等效電路就是圖一(b)所示的基本同相比例電路,利用疊加原理得P點開路電壓 Us=1/3(Ui1+Ui2+Ui3),電壓源等效內阻R0=R//R//R;直接套用基本同相比例電路的公式,可得:
Uo=(1+R/0.5R)*Us=Ui1+Ui2+Ui3 , 輸出為三個輸入信號的同相疊加。
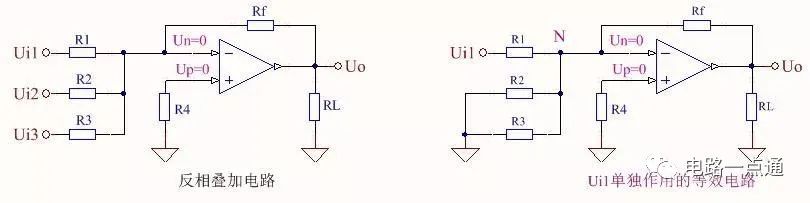
圖三 反相疊加與等效電路
圖三為信號反相疊加電路,其輸出等于各個輸入信號單獨作用時的輸出之和,當Ui1單獨作用時,將Ui2、Ui3對地短路,此時的等效電路 如圖三右側所示。因同相端接地,反相端為虛地點,即N點為零電位,R2、R3上沒有電流,可以認為R2、R3 存在與否對電路無影響,即可以拿掉,等效電路就和圖一(a)的基本反相比例電路相同,直接套用反相比例電路公式,得Ui1單獨作用時的輸出:Uo1=-Rf/R1*Ui1 ; 同理可得:Uo2=-Rf/R2*Ui2 ; Uo3=-Rf/R3*Ui3 ; 總輸出Uo=Uo1+Uo2+Uo3 ;當Rf=R1=R2=R3時, Uo=-(Ui1+Ui2+Ui3),完成了輸入信號的反相疊加。
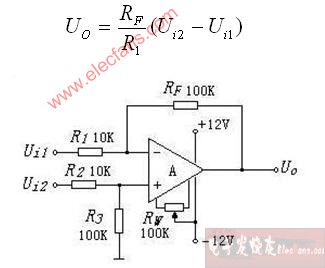
二.采用不同思路可構成不同的求差電路。用信號反相并求和的思想,可以得到圖四所示的減法電路。
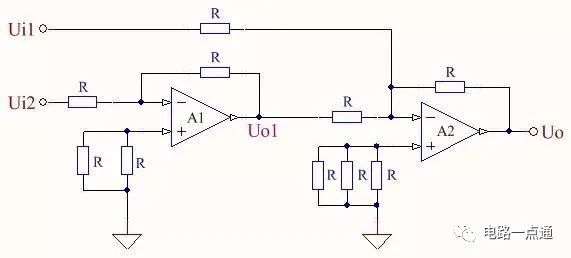
圖四 信號反相與疊加實現的求差電路
該電路由兩級運放構成,其中A1構成反相器,A2構成兩信號反相疊加電路,圖中運放同相端并聯的電阻,是為了運放兩輸入端的電阻平衡。第一級輸出Uo1=-Ui2 ; 按圖三反相疊加電路的結論,得該電路輸出為:Uo=-(Uo1+Ui1)=Ui2-Ui1 ,實現了信號的求差運算。
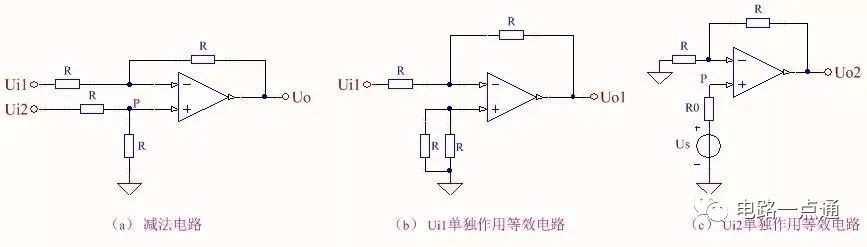
圖五 差分電路實現的求差電路
圖五是按同相比例和反相比例相結合的思想,利用差分電路構成的求差電路,與圖四相比,只用一個運放單元,但該電路不能用虛地概念,運放兩輸入端存在共模電壓,實際使用時,應盡量選高共模抑制比的運放。當Ui1單獨作用時,等效電路如圖五(b)所示,為基本反比例電路,此時Uo1=-Ui1 ; 當Ui2單獨作用時,利用戴維南定理,將電路等效為圖五(c)所示電路,其為基本同相比例電路,P點開路電壓Us=R/(R+R)*Ui2=0.5Ui2 ; 等效電源內阻R0=R//R ; 直接套用同相比例電路公式, 得Uo2=(1+R/R)*Us=Ui2 ; 電路輸出Uo=Uo2+Uo1= Ui2-Ui1 ; 實現了信號求差運算。
-
運算電路
+關注
關注
8文章
117瀏覽量
27064 -
電壓
+關注
關注
45文章
5696瀏覽量
117256 -
接地
+關注
關注
7文章
812瀏覽量
46392
原文標題:信號疊加和求差電路
文章出處:【微信號:硬件測試雜談,微信公眾號:硬件測試雜談】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
比例求和運算電路實驗
比例運算電路:同相比例運算電路與反向比例運算電路的區別
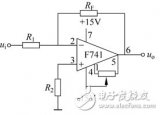





 比例運算電路基本拓撲結構
比例運算電路基本拓撲結構











評論