摘 要：精確的位置信息在無線傳感網絡（WSNs）中扮演著重要地位，基于用戶節(jié)點之間信息交互的協(xié)同定位可以提供高精度定位，是目前非常有前景的研究方向。傳統(tǒng)的協(xié)同定位模型，例如最小二乘（LS）模型，依賴于從先驗測量信息中得到粗略的位置估計作為迭代初值。由于代價函數一般為非凸，該模型對迭代初值的選取十分敏感，計算結果容易陷入局部極值。為了深入解釋這一現(xiàn)象，文中通過求取最小二乘代價函數的二階導數，同時對相應的 Hessian 矩陣進行相似變換，分析了最小二乘代價函數的凸性，得出最小二乘代價函數為凸的一個充分不必要條件。同時利用數值仿真驗證了當用戶節(jié)點測距偏差全部為負數時，最小二乘代價函數在全局范圍內為凸函數，這一結論為后續(xù)研究奠定了理論基礎。

0 引 言

實時高精度位置感知在無人機技術、醫(yī)療服務、搜索救援、智能圖書館、自動駕駛等領域中有著廣泛的應用［1?3］。近年來，作為傳統(tǒng)無線傳感網絡（WirelessSensor Networks，WSNs）定位方法的補充，協(xié)同定位受到越來越多的關注。所謂的協(xié)同定位是指多用戶節(jié)點之間的協(xié)同，與傳統(tǒng)定位方法相比，該方法增加了用戶節(jié)點之間的幾何測量與通信。協(xié)同定位算法有很多，基于到達時間（Time of Arrival，TOA）的極大似然估計模型是應用最為廣泛的定位模型之一，當測距誤差服從高斯分布 時 ，極 大 似 然 模型與最小二乘估計模型（LeastSquare，LS）等價［4］。為了求得該模型的最優(yōu)解，比較常見的算法為牛頓迭代法或高斯?牛頓迭代法。文獻［5］給出了這兩種算法的收斂性證明，指出收斂性與代價函數的凸性緊密相關，當目標函數為嚴格凸時（Hessian矩陣正定），由牛頓算法解算LS模型為強整體二階收斂。

劃分一個優(yōu)化問題難易程度的分水嶺在于其代價函數是凸或者非凸［6］，而 LS 定位模型的代價函數一般為非凸，因此求解LS定位模型代價函數的全局最優(yōu)解是困難的，屬于NP難問題，目前已有相關研究嘗試對這一個問題進行解決。文獻［7?8］對單用戶定位場景下的LS 模型進行了深入分析，提出了代價函數滿足全局為凸的條件。LS模型基于最小方差準則（這一準則也是其他定位模型的基礎），例如極大似然、加權最小二乘、遞推最小二乘等。與此同時，相比遞推最小二乘，卡爾曼濾波（Kalman Filtering，KF）模型相當于在兩次迭代之間多了狀態(tài)轉移步驟，其核心也是通過最小化方差求得最優(yōu)估計［9］。因此，對LS定位模型的凸性進行分析具有一定的代表性，其相關結論可以通過最小方差準則推廣到其他定位模型。

在協(xié)同場景中，當用戶節(jié)點數量增多時，函數的局部極值點增多，使得迭代算法對初值更加敏感并導致算法不收斂。本文將對協(xié)同定位LS模型的凸性進行分析，以深入解釋這一現(xiàn)象。

1 無約束最小二乘定位模型

1.1 節(jié)點與鏈路定義

在基于TOA方法的定位場景中，設用戶節(jié)點個數為M，用Fc={T1 ， T2 ，?， TM}表示其編號的集合，用戶節(jié)點真實坐標為xj∈Rη，1≤j≤M，j∈N+，η∈N+為定位場景歐幾里得空間維度。錨節(jié)點的個數為N，其編號的集合為Fa={A1，A2，?，AN}，錨節(jié)點真實坐標為si ∈Rη，1≤i≤N ，i∈N+。設所有節(jié)點的集合記為Ft，則Ft =Fa?Fc。在定位場景中，定義任意兩點之間的距離觀測為一條測距鏈路，假設某個場景中共有 L 條測距鏈路，記各個鏈路編號的集合為L={l1 ， l2 ，?， lL}。定位場景中的測距鏈路可以分為兩類：一類為用戶與錨節(jié)點之間的測距鏈路（以下簡記為 AT 鏈路）；另一類為協(xié)同測距鏈路（以下簡記為 TT 鏈路）。設所有鏈路距離觀測值的集合記為 Dt，其中 AT鏈路距離觀測值的集合記為 Da，TT鏈路距離觀測值集合記為Dc，易知Dt=Da?Dc，Da?Dc=?，并且有|Dt=L|，|Da=N|，|Dc= L - N|。令dK1K2是節(jié)點編號 K1到 K2點的真實距離，dK1K2為兩點之間距離的估計值，其中 K1 ，K2 ∈ Ft。

1.2 測距偏差定義

由于信號在傳播過程中會受到觀測噪聲、多徑效應以及非視距（Non?Line of Sight，NLOS）傳播的影響，觀測值不等于節(jié)點之間的真實距離，存在測距偏差。設偏差向量為ε=［ε1，ε2，?，εL］T∈RL，其中εi表示第i條鏈路上的測距偏差。在視距（Line of Sight，LOS）傳播環(huán)境中，測距偏差完全由觀測噪聲引起，其通常滿足均值為零、方差為常數的高斯分布，用εLOS表示。在NLOS環(huán)境中，除了噪聲以外還存在一個正偏差，假設此正偏差滿足均值和方差都為常數的高斯分布，用εNLOS表示。基于以上假設，可以對測距偏差建模如下：

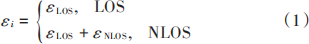
式中：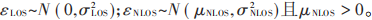

1.3 最小二乘模型定義

在非協(xié)同定位場景中，假設有M個用戶節(jié)點，且任意兩個用戶節(jié)點之間無測距和數據交互。考慮某一用戶節(jié)點Tj，其位置的真實值為xj，令xj表示Tj節(jié)點坐標的估計值，則有：

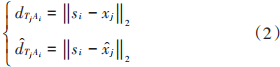
式中2表示兩點之間的歐幾里得距離。

若測距鏈路個數為N，分別記為l1 ， l2 ，?， lN，令與之相對應的距離真實值與估計值分別為di和di，且有：

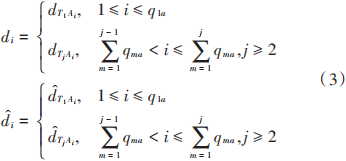
式中：1≤i≤N， i∈N+；qja是與節(jié)點Ti 相連接的鏈路個數。設距離觀測值為ρi∈Da ， 1≤i≤N， i∈N+，如果考慮偏差的存在，由定義可知，距離觀測值與真實距離之間的關系為：

那么非協(xié)同場景中無約束LS估計模型可以表示成如下形式：

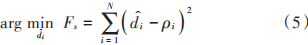
在非協(xié)同場景中，設Tj節(jié)點真實坐標和坐標估計值分別為xj和xj，那么有：

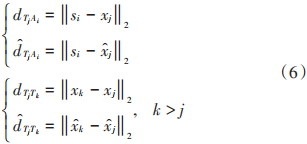
設測距鏈路有L條，分別記為l1 ， l2 ，?，lN，與之相對應的距離真實值與估計值分別記為di和di 。若1≤i≤N，li為AT鏈路，按照式（3）對di和di 進行賦值。若N《i≤L，li為TT鏈路，按照式（7）進行賦值：

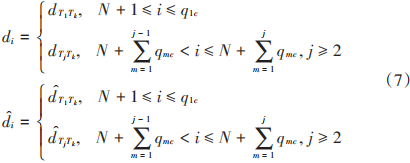
式中：qjc是鏈路端點為Tj Tk且滿足k》j的TT鏈路個數，Tk∈Uj，k》j，j≥2，Uj為與Tj之間存在測距鏈路的用戶節(jié)點的集合，其元素下標按由小到大的順序進行排列。令Tk為 Uj中第g個元素，且 g的值按照式（8）進行計算：

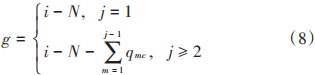
設ρi∈Dt， 1≤i≤L， i∈N+ 為距離觀測值，其與真實距離之間的關系滿足式（4）。在此基礎上構建協(xié)同場景無約束LS模型為：

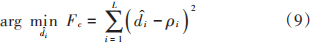
在本文中統(tǒng)一稱Fs和Fc為LS定位代價函數并且將其記為F。

2 模型的非凸性分析

2.1 非協(xié)同定位場景分析

為了便于分析且不失一般性，本文選取η=2。由凸分析相關理論可知，函數的凸性與其Hessian矩陣密切相關，并且有如下定理成立：

定理1［6］：函數為凸的二階條件。假設x的函數f二階可微，定義域domf為凸集且Hessian矩陣存在，則函數在domf中為凸的充要條件為：對于?x∈domf，其Hessian矩陣為半正定矩陣。

首先求取代價函數Fs的梯度（一階微分）和Hessian矩陣（二階微分），計算結果分別如下：

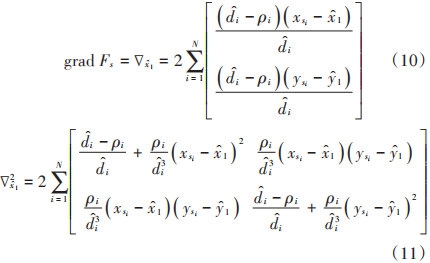
運用定理1可以得出以下推論：推論1：當LS代價函數的dom Fs為R2時，其定義域為凸集。令?2x1?0，設滿足此條件的所有x1的集合為A，則當x1∈A時，F(xiàn)s為凸函數。

上述推論給出了LS代價函數為凸的一個充分必要條件。?2x1為實對稱矩陣，關于實對稱矩陣有以下兩個引理成立：

引理 1［10］：實對稱矩陣的特征值均為實數。

引理 2［10］：實對稱矩陣是半正定矩陣的充要條件為其所有特征值非負。

由引理2可知，對?2x1半正定的判斷可以轉化為對其特征值正負的判斷。設J=?2x1，J∈R2 × 2，令Jij 為J 中各個元素，設J的特征值為λ，其特征多項式為：

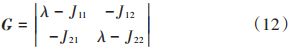
令G=0，可以得到特征多項式方程為：

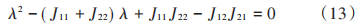
式（13）為一元二次方程，由引理1可知，此方程必存在2個實根，即根的判別式Δ≥0恒成立，函數2個非負實根的充分必要條件為：

推論2：所有滿足不等式組（14）條件的x1的集合為A。

推論2是LS代價函數為凸的一個等價條件。然而，由于不等式組（14）的非線性特征，使得對該不等式組分析變得比較困難。下面將針對一類特殊的情況進行討論，并且作出簡要證明。

命題1：存在一個集合C，若該集合中所有估計值x1均滿足di-ρi ≥ 0，則在此集合中最小二乘代價函數Fs為凸，且滿足C?A。

引理3：有限個半正定矩陣的和仍為半正定矩陣。即若Ri?0， 1≤i≤N， i∈N+，則有W=∑i=1N，Ri ? 0。

考慮對J進行分解，并且令J =∑i =1NQi

其中：

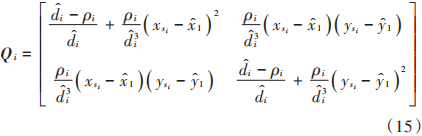
對Qi求特征值，令：

化簡得：

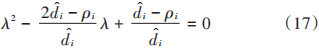
因式分解可求得λ的2個根分別為：

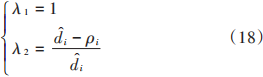
從式（18）中可以看出，矩陣Qi有2個特征向量，其中λ1》0 恒成立，所以當λ2=di-ρi ≥0時，Qi ?0。由引理3易知，當di-ρi≥0， 1≤i≤N， i∈N+ 成立時，J?0。所有滿足此條件的估計值x1的集合即為C。

命題1實際上是Fs局部為凸的一個充分不必要條件，F(xiàn)s的非凸區(qū)間會隨著εi 的增大而減小，且當滿足εi》0的測距鏈路數量增多時，F(xiàn)s的非凸性也會增強。

2.2 協(xié)同定位場景分析

在協(xié)同場景中，測距鏈路由AT鏈路和TT鏈路兩部分組成。受引理3的啟發(fā)，將Fc的 Hessian矩陣J分解為若干個子矩陣Qi，每一個Qi 實際上是一個與估計值相關的函數f（di）=（di-ρi2），子矩陣中的各個元素為f（di）對用戶節(jié)點坐標的二階偏導。在2.1節(jié)中，證明了當li為AT鏈路時滿足命題1，接下來說明當li為TT鏈路也具有類似于命題1的性質。為了便于分析，選取協(xié)同場景中的某一條TT鏈路lk，記此鏈路兩端的用戶節(jié)點為Tm，Tn。其估計值分別為（xm，ym），（xn，yn），測距觀測值為ρk，此時LS代價函數為：

分別對xm，xn，ym，yn求偏導，可得梯度向量（一階微分）為：

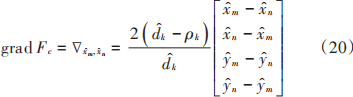
則Hessian矩陣為：

求取J 的特征值，通過計算可以求得其特征多項式為：

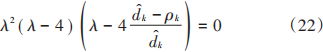
可以解得其4個特征值分別為：

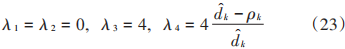
由式（23）可知，當dk-ρk≥0時，J?0。接下來做進一步地推廣，證明當LS代價函數中同時具有兩種測距鏈路時，這一性質仍然不變。

設協(xié)同場景中有M個用戶節(jié)點，記Fc的Hessian矩陣為J ，易知J∈R2M×2M 。對J進 行分解，并且令J=∑i=1LQi。其中，Qi 為每一個測距鏈路對應的Hessian矩陣。

引理4［11］：相似矩陣具有相同的特征值。

若測距鏈路位于錨節(jié)點與待定位節(jié)點之間，則Qi的元素位于對角線和與之相鄰的位置上，且元素的個數為4，將 Qi 中的4個元素全部平移至左上角。設變換后的矩陣為Qi′，易知 Qi 與 Q i′ 為相似矩陣。由引理4可知Qi 與Qi′具有相同的特征值。設Gi′=λI-Qi′，為了求取G ′的特征值，對G ′作如下分塊：

式中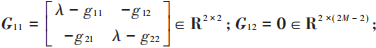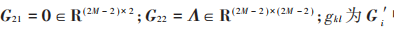：中第k行l(wèi)列元素。

由分塊矩陣行列式定理可知［11］：

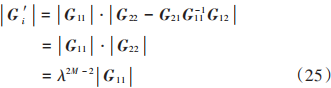
令|Gi′|=0，由非協(xié)同場景分析可知，|G11|=0的2個解分別為λ=1和λ=di-ρidi，|Gi′| 0的剩余（2M-2）個解均為 0。因此，當di -ρi≥0時，Qi?0。

若測距鏈路位于兩個待定位節(jié)點之間，易知Qi 中的元素個數為16個，將其中各個元素全部平移至左上角，將其記為Qi′，設Gi′=λI-Qi′。同樣地，對Gi′進行分塊：

式中：

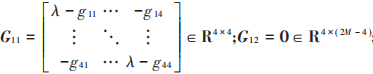
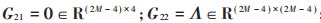
gkl為Gi′中第k行l(wèi)列元素。

由分塊矩陣行列式定理可知：

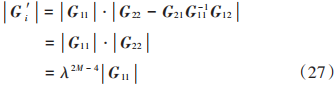
令|Gi |=0。由協(xié)同鏈路分析可知，|G11|的特征值有4個，分別為λ1=λ2=0，λ3=4以及 λ4=4di-ρidi，|Gk′|=0 剩余（2M-4）個解均為0。因此，當di-ρi≥0時，Qi?0。

命題1指出，在滿足di-ρi≥0這一條件時，總可以找到合適的區(qū)間，在區(qū)間中LS代價函F為凸。

命題2：對于?i ， 若di-ρi≥0在x?=［x1，x2，?， xM ］T∈R2M上恒成立，則F在R2M上為凸函數。

命題2是LS代價函數全局為凸的一個充分不必要條件。在實際場景中，當測距偏差大于 0時，距離觀測值ρi為正，在此情況下不滿足全局為凸的條件，若εi≤-di，則ρi≤0，此時di-ρi≥0恒成立，F(xiàn)s在全局范圍內為凸。

3 仿真驗證

3.1 仿真場景設定

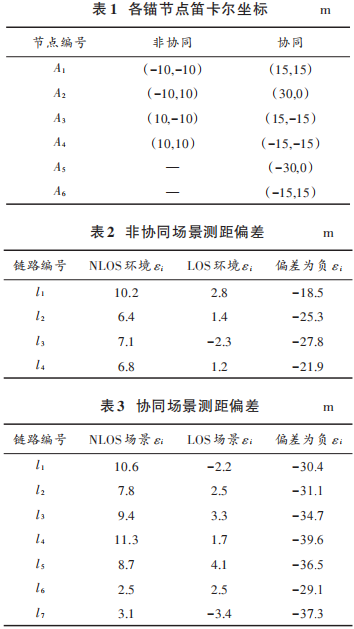
在二維平面內建立笛卡爾坐標系，表1給出了非協(xié)同與協(xié)同場景各個錨節(jié)點的平面坐標。本節(jié)將對三種偏差環(huán)境進行仿真，分別為NLOS環(huán)境、LOS環(huán)境以及測距偏差為負的情形。每一個場景在各種情況下的偏差大小如表2和表3所示。

3.2 凸性驗證

首先對Fs作全局仿真。考慮測距誤差不同的情況下代價函數Fs的凸性，作出其函數圖像、Hessian矩陣J的正定圖像以及選取不同初值的迭代情況，仿真結果如圖1~圖3所示。

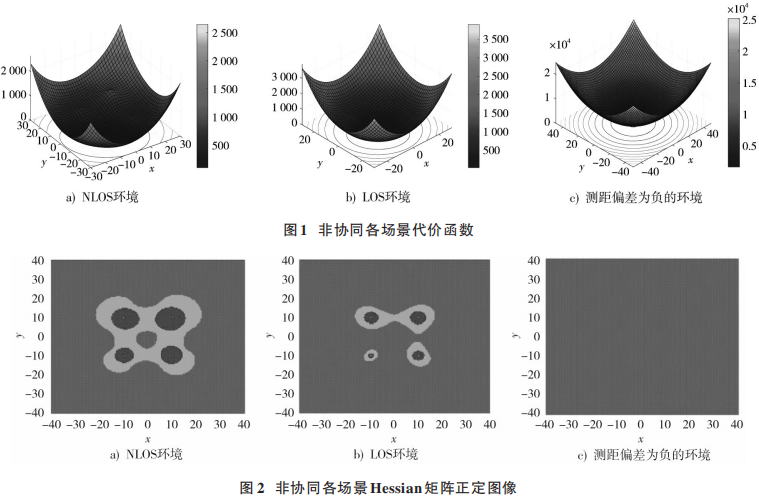
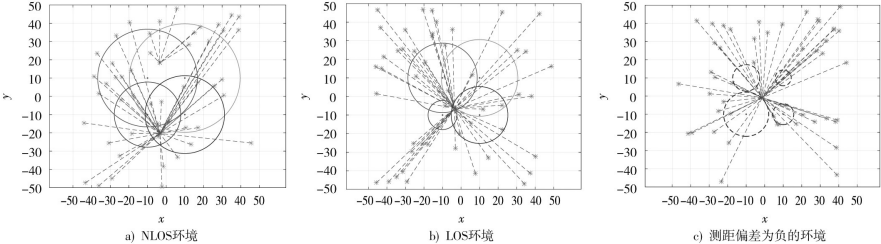
圖1分別顯示了NLOS環(huán)境、LOS環(huán)境以及測距偏差為負的環(huán)境下LS代價函數圖像。

圖2分別顯示了二維平面中各個點Hessian矩陣J的半正定情況，其中紅色部分表示J?0，藍色部分表示J?0，綠色部分表示不定。

由定理1可知，當J為半正定時，函數為凸。從圖2a）中可以看出，當定位環(huán)境為 NLOS 環(huán)境時，J的半正定區(qū)域不連續(xù)，不定與半負定面積總和較大，當定位環(huán)境為LOS環(huán)境時，J的半正定區(qū)域連續(xù)，不定與半負定面積總和較小。由命題2可知，當存在正的測距誤差時，則代價函數 Fs 在全局范圍內為非凸，因此在上述的兩個定位環(huán)境中，F(xiàn)s 在全局范圍內均為非凸，如圖1a）和圖1b）所示。當測距誤差為負且絕對值較大時，滿足命題2中代價函數 Fs 為凸的全局條件，如圖1c）和圖2c）所示，由J 的半正定性和Fs函數圖像可以看出，J在全局范圍內半正定且 Fs在全局范圍內為凸函數。

為了說明初值選取對迭代結果的影響，從各個方向選取不同的初值，用高斯?牛頓迭代法進行位置解算。解算結果如圖3所示，其中虛線構成的圓表示測距半徑為負，其大小為距離觀測值的絕對值。從仿真結果可知，在NLOS環(huán)境中，LS代價函數Fs為非凸函數，存在多個極值點，當初始值不同時迭代算法會收斂到不同的極小值點；在LOS環(huán)境中測距偏差較小，LS代價函數在全局范圍內為非凸，但其極值點個數并沒有增加，在這種情況下迭代算法會收斂于同一個位置，說明LS模型在LOS場景中適用；在偏差為負的場景中，迭代結果與初始位置無關，驗證了在此情況下Fs具有全局收斂的特性。

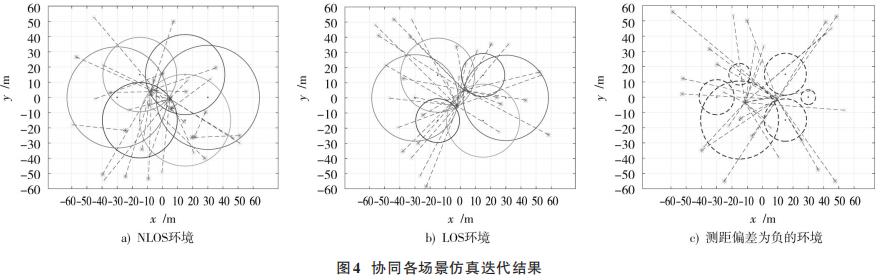
在協(xié)同場景中，選取不同的初值，利用高斯?牛頓迭代算法解算用戶位置，仿真結果分別如圖4所示。在NLOS定位環(huán)境中，由于存在較大的正測距誤差，使得Fc在全局范圍內非凸并且導致產生了多個極值點，因此不同的初始值會導致算法迭代收斂到不同的極值點上；在LOS定位環(huán)境中，F(xiàn)c在全局范圍內為非凸，但正測距偏差較小，因此仍然可以收斂到相同的極值點上；在測距偏差為負的情況下，F(xiàn)c在全局范圍內為凸，因此無論初值如何選取，其必然會收斂到全局最優(yōu)解。此結果較好地驗證了命題2的正確性。

4 結 語

本文對協(xié)同定位無約束LS定位模型進行了凸性分析。通過對代價函數的 Hessian矩陣的分析，得出了無約束LS代價函數的一個充分不必要條件，該條件指出，當測距偏差全部為負時，無約束LS定位代價函數全局為凸。在此基礎上，分別對NLOS環(huán)境、LOS環(huán)境以及測距偏差為負環(huán)境下的LS代價函數凸性進行了仿真分析，驗證了該命題的正確性。除此以外，本文提出影響最小二乘代價函數非凸性的主要因素為正測距偏差，為后續(xù)研究奠定了理論基礎。

審核編輯 ：李倩