上次介紹了與、或、非門。這次我們講講這些門能用來做什么。
《加法器》(實現兩數相加)
我們考慮以下幾種情況(以下數字皆為二進制數)。
0+0=0 零加零毫無疑問等于0。
0+1=1 1+0=1 這個應該也不用解釋。
1+1=10 2的二進制數寫作10,所以也沒有什么問題。
我們可以繪制出這樣一張表。其中A和B為輸入(加數),C(和)和D(進位)為輸出。
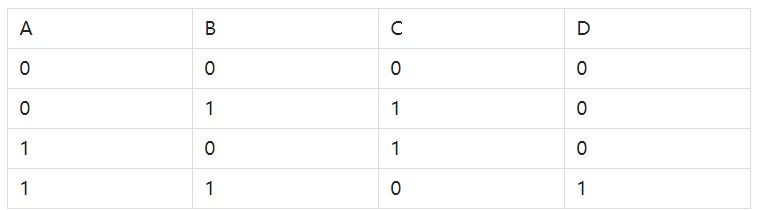
我們可以用以下電路來滿足這張表(真值表)
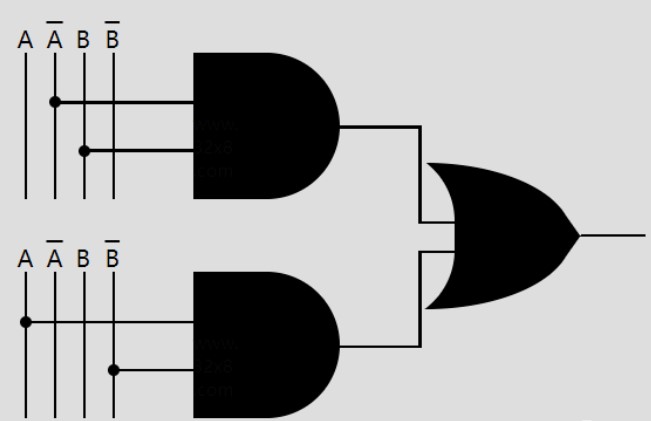
解釋一下,A上有一條橫線則意為A的取反。如果A是0,那么A-就是1。最右邊的則是C本位求和輸出。本圖中沒有D輸出,D輸出放在下圖中討論。我們來試一下真值表的第一行。
第一行中A和B數值均為0,A-為1,故第一路與門輸出為0,同理第二路輸出也為0。兩條與門輸出作為或門的輸入,故與門的輸出也為0。剩下的幾行你們可以自己試試看。
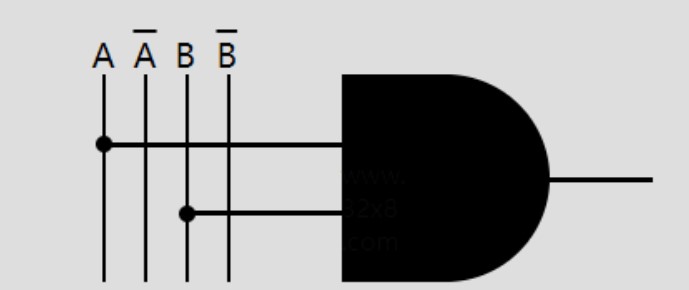
這張圖是D的進位輸出。可以從真值表很容易觀察得到D與A和B的關系就是與門的關系,所以很容易畫出這個電路。
既然本位相加和進位信號都有了,那么我們便可以設計出下圖這樣的加法器:
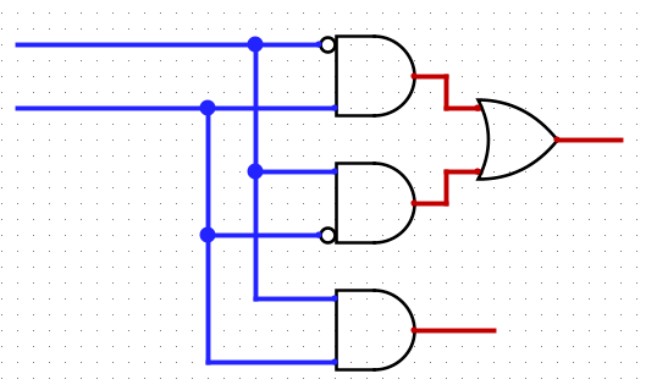
左邊兩根藍線從上至下分別是A和B輸入。右邊兩根紅線從上至下分別是C和D輸出。
這個電路被稱為半加法器。如果我們要算的數值有三位,那么我們就串聯三個這樣的電路就可以實現四位的加法。注意不是簡單串聯,本位的進位要與下一位的和相加。
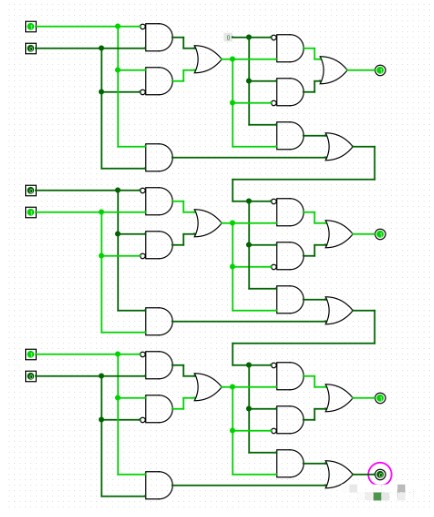
這是三位加法器,其中加數分別是101(5)和10(2),和是111(7)右下角粉紅圈中的是溢出信號(最高位的進位信號),第一位數字沒有前一位的進位信號,所以你可以在圖中的上半部分看到一個特別的常數0。注意:不要將該電路誤解成并聯,其實質還是串聯。你們可以跟著門電路和二進制加法琢磨琢磨其本質。
其中減法比較巧妙,它在加法的基礎上稍加改動而來。
比如101(5)-010(2)=011(3)我們把減數010按位取反,變成101,再在末尾加1,變成110。我們發現101+110=1011,若把最高位的數字舍去,剩下的便是差011。
再例如110110(54)-100100(36)=010010(18)。100100按位取反,變成011011,加1,變成011100。110110+011100=1010010,最高位舍去,得010010(18)。
你們可以隨便寫幾個數試試,感受一下這個方法的巧妙之處。
不單單是加減運算,邏輯門還可以實現乘除、開方、指對等運算,可以勝任圖像處理、數據檢索、人工智能等任務。
重頭戲還在后頭呢。
審核編輯:劉清
-
邏輯門
+關注
關注
1文章
142瀏覽量
24734 -
加法器
+關注
關注
6文章
183瀏覽量
30578
發布評論請先 登錄





 講講與、或、非門都能用來做什么
講講與、或、非門都能用來做什么










評論