1 連續周期信號的傅里葉分解
信號的正交分解 -- 在區間上的任意能量有限信號f(t)可以用正交函數集合 中的函數的線性組合來近似表示:
式中:表示正交函數集中的函數,系數可以利用最小均方誤差準則求解:
常用的完備正交函數集:
三角函數集{}
復指數函數集{}
信號在這兩個函數集中分解得到的級數叫做傅里葉級數,周期信號進行傅里葉分解應該滿足狄利克雷條件:
在一個周期內滿足絕對可積
在一個周期內有有限個極大值和極小值
在一個周期內有有限個第一類間斷點
三角傅里葉級數設f(t)為一周期為T的周期信號,且滿足狄氏條件,則f(t)在區間可分解為:
式中:
T為信號周期,為基波頻率(看作整體一項)。
寫作余弦形式:
式中:
為偶函數,為奇函數。
指數傅里葉級數設f(t)為一周期為T的周期信號,且滿足狄氏條件,則f(t)在區間可分解為:
式中:
指數傅里葉級數中負頻率的出現是數學處理的結果。
復振幅表示式中,表示n次諧波分量的復振幅。
2 連續非周期信號的傅里葉變換周期信號的頻譜具有離散性,非周期信號的頻譜變為連續譜。
非周期信號傅里葉變換存在的充分條件是信號滿足絕對可積,即:
正變換:
反變換:
與周期信號相比,中自變量連續取值,而離散取值,且滿足:
若信號不滿足絕對可積條件,其傅里葉變換就不存在,此時拉普拉斯變換適用,略。
3 周期序列的離散傅里葉級數(DFS)時域的周期造成頻域的離散,時域的離散造成頻域的周期延拓,因此周期序列的DFS也是離散的周期序列。
周期序列:
式中,r為任意整數,N為周期。DFS正變換:
DFS反變換:
式中,從DFS計算中可以看出,周期序列的DFS也是周期為N的離散序列,周期序列的DFS也具有無限個頻率,僅有N個不同幅值。
4 離散傅里葉變換(DFT)長度為N的序列x(n)可以看作:
式中,表示長度為N的單位矩形序列。叫做的主值序列。DFT正變換:
DFT反變換:
從DFT的計算中可以看出,DFT的結果對應DFS一個周期的序列值。
-
頻譜
+關注
關注
7文章
893瀏覽量
46298 -
函數
+關注
關注
3文章
4367瀏覽量
64165 -
傅里葉
+關注
關注
0文章
60瀏覽量
20782
原文標題:信號的分解
文章出處:【微信號:zhuyandz,微信公眾號:FPGA之家】歡迎添加關注!文章轉載請注明出處。
發布評論請先 登錄
VirtualLab:光柵的優化與分析
VirtualLab 應用:薄元近似(TEA)與傅里葉模態法(FMM)的光柵建模
VirtualLab Fusion應用:元件內部場分析儀FMM
VirtualLab Fusion應用:抗反射蛾眼結構的仿真
VirtualLab Fusion案例:單分子顯微鏡高NA成像系統的建模
VirtualLab Fusion案例:高NA傅里葉單分子成像顯微鏡
低壓配電中產生的諧波應該如何治理?
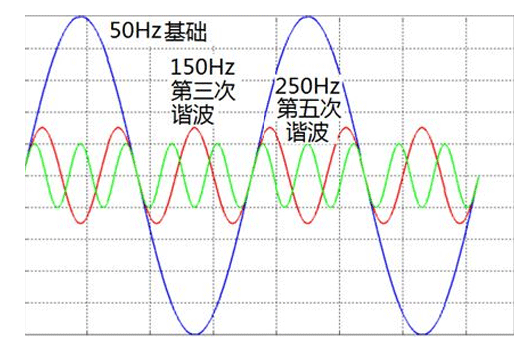
傅里葉變換的數學原理
無葉風扇燈的優缺點有哪些
傅里葉半導體榮獲季豐電子AEC-Q100與AEC-Q006證書
FIR連續采樣分段卷積時域重疊相加法





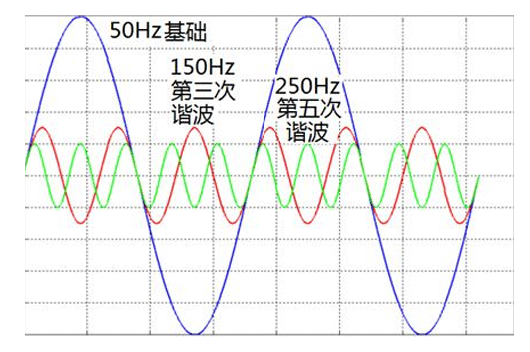
 連續周期信號的傅里葉分解
連續周期信號的傅里葉分解










評論