這是工作中遇到的小問(wèn)題。
數(shù)據(jù)結(jié)構(gòu)中有一種數(shù)據(jù)類(lèi)型——堆棧,該結(jié)構(gòu)中的數(shù)據(jù)項(xiàng)有如下特點(diǎn):
除了最前面和最后面的數(shù)據(jù),每個(gè)數(shù)據(jù)項(xiàng)都有一個(gè)前驅(qū)結(jié)點(diǎn)和一個(gè)后繼結(jié)點(diǎn);
堆棧兩端分別稱(chēng)為棧頂和棧底,數(shù)據(jù)項(xiàng)只能在棧頂加入或者彈出。
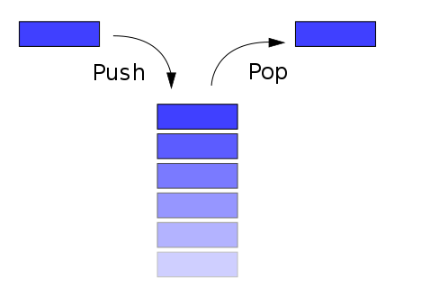
很明顯,堆棧的數(shù)據(jù)遵循先入后出原則。假設(shè)我們有 3 個(gè)不同的數(shù)據(jù)項(xiàng),編號(hào) 1,2,3,只要保證入棧順序是大編號(hào)在后小編號(hào)在前,且每次進(jìn)棧的數(shù)量不限,則所有可能的出棧順序有:1-》2-》3,1-》3-》2,2-》1-》3,2-》3-》1,3-》2-》1 一共 5 種,注意 3-》1-》2 不是可能的出棧順序,因?yàn)槿绻?3 最先出棧,那么 1 和 2 必在棧中(如果還未入棧,則說(shuō)明 3 先入棧,與假設(shè)矛盾),只能 2 在上 1 在下,所以出棧順序必然是 2-》1。那么,
問(wèn)題一:編號(hào)\(1\sim n\)的連續(xù)數(shù)據(jù)項(xiàng)以編號(hào)的先后順序入棧然后出棧,所有可能的出棧順序有多少種?
上面的問(wèn)題比較難于回答,引申之后得到另一個(gè)比較弱的問(wèn)題
問(wèn)題二:給定一個(gè)長(zhǎng)度為\(n\) 的整數(shù)序列,且各個(gè)元素均不相同,它是否是一個(gè)出棧序列?
為了回答以上的兩個(gè)問(wèn)題,我們首先來(lái)看下一個(gè)正常的出棧序列有什么特點(diǎn)。假設(shè)長(zhǎng)度為 \(n\)的出棧序列是\(a_1,a_2,…,a_n\),取其中第\(k\) 個(gè)數(shù) \(a_k\),則有如下結(jié)論:
\(a_k\)之前的所有數(shù)據(jù)項(xiàng)都已經(jīng)出棧,即\(a_1,a_2,…,a_{k-1}\)都已經(jīng)出棧;
\(a_k\) 之后的所有數(shù)據(jù)項(xiàng)中,小于 \(a_k\)的都在棧內(nèi),大于\(a_k\)的尚未入棧;
\(a_k\)之后緊跟的出棧數(shù)據(jù)項(xiàng) \(a_{k+1}\) 要么大于\(a_k\),要么是所有未出棧的比\(a_k\)小的數(shù)據(jù)項(xiàng)中最大的一個(gè)
結(jié)論 1 很明顯,因?yàn)楸旧砭褪浅鰲P蛄校虼酥暗臄?shù)據(jù)肯定已經(jīng)出棧;結(jié)論 2 中,之后的數(shù)據(jù)只有兩種存在的可能:在棧內(nèi),或者未進(jìn)棧。比\(a_k\)小的如果未進(jìn)棧,那么 akak 根本不可能出棧(因?yàn)榫蜎](méi)進(jìn)棧),比\(a_k\)大的如果在棧內(nèi),那\(a_k\)也無(wú)法出棧,因?yàn)閈(a_k\)在它的下面,因此得證;結(jié)論 3,\(a_{k+1}\)就是\(a_k\) 出棧后棧頂?shù)臄?shù)據(jù),因此必然是在棧內(nèi)的數(shù)據(jù)的最上面的一個(gè),或者是棧外的某一個(gè)數(shù)據(jù)(進(jìn)棧再出棧)。
于是由結(jié)論 3 找到判斷序列的方法:逐個(gè)檢查序列的每一項(xiàng)\(a_k\),將該項(xiàng)之后的數(shù)據(jù)分為大于該數(shù)據(jù)的大數(shù)集合\(S_g\)和小于該數(shù)的小數(shù)集合\(S_l\),查看是否后續(xù)的數(shù)據(jù)項(xiàng)是小數(shù)集合的最大值或者是大數(shù)集合的任意值,如果不是則不是出棧序列,即若 \(a_{k+1}\in S_g\) 或 \(a_{k+1}=max_l{S_l}\),即是出棧序列。
問(wèn)題一的解答,就是窮舉長(zhǎng)度為 nn 的序列,逐個(gè)進(jìn)行判斷,得到最后的結(jié)果,附上 python 程序。
import math
import itertools
% 輸入序列的長(zhǎng)度
n = raw_input(“Input n: ”)
% 判斷是否是出棧序列
def IsNotStackSeq(n_ls, n):
for k in range(0,n-2):
% 逐個(gè)檢查序列中的每一個(gè)元素
ak = n_ls[k]
set_in = n_ls[k+1:]
a_max = ak
% 將ak之后的元素分為大于和小于兩組集合
min_list = [item for item in set_in if item 》 ak]
max_list = [item for item in set_in if item 《 ak]
if len(max_list) 》 0:
a_max = max(max_list)
% 后續(xù)的元素是否是小于集合的最大值或者屬于大于集合
if n_ls[k+1] != a_max and (n_ls[k+1] not in min_list):
return 1
return -1
def StackSeqList(n):
n_permation = list(itertools.permutations(range(1,int(n)+1), int(n)))
n_list = [item for item in n_permation if IsNotStackSeq(list(item),int(n)) 《 0]
return (len(n_list),n_list)
編輯:hfy
-
堆棧
+關(guān)注
關(guān)注
0文章
183瀏覽量
20024 -
數(shù)據(jù)結(jié)構(gòu)
+關(guān)注
關(guān)注
3文章
573瀏覽量
40575 -
python
+關(guān)注
關(guān)注
56文章
4823瀏覽量
86060
發(fā)布評(píng)論請(qǐng)先 登錄
c++之棧和隊(duì)列
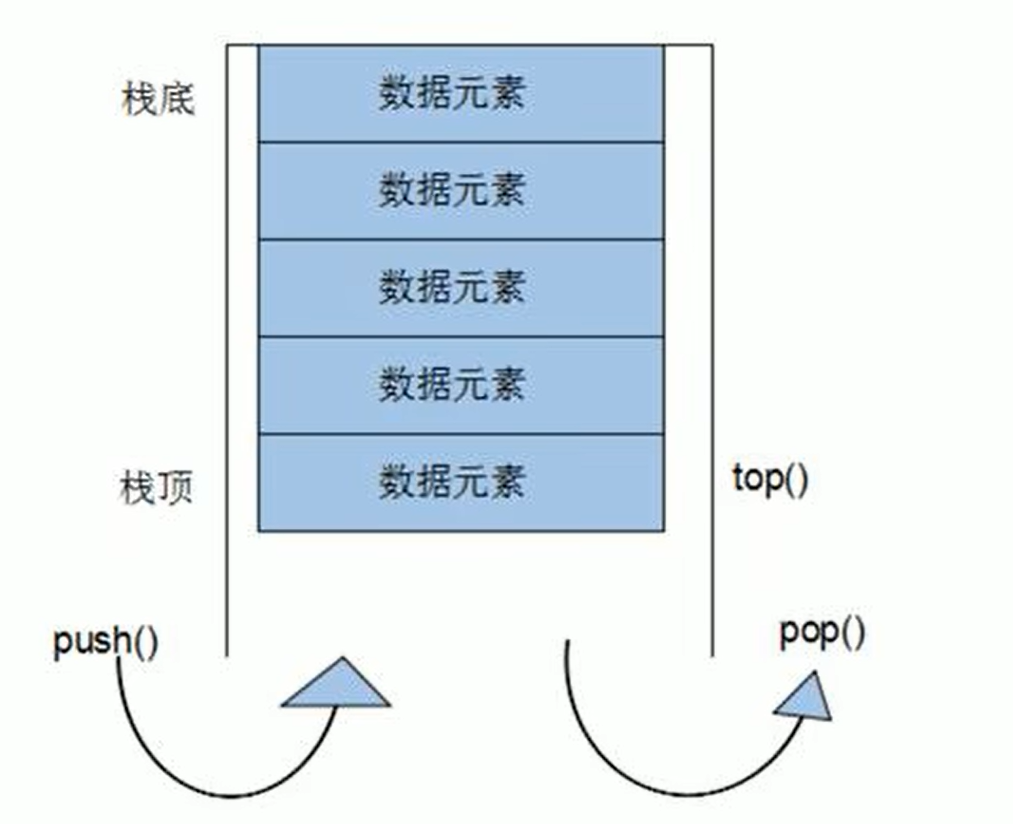
數(shù)據(jù)結(jié)構(gòu)的幾個(gè)重要知識(shí)點(diǎn)
UCOSIII任務(wù)堆棧和STM32堆棧增長(zhǎng)方向是否一致?
常見(jiàn)的數(shù)據(jù)結(jié)構(gòu)
數(shù)據(jù)結(jié)構(gòu)之鏈?zhǔn)?b class='flag-5'>棧介紹
STM32堆棧區(qū)劃分
計(jì)算機(jī)堆棧有哪些功能
java數(shù)據(jù)結(jié)構(gòu)學(xué)習(xí)
堆和棧有什么區(qū)別堆棧的詳細(xì)資料說(shuō)明
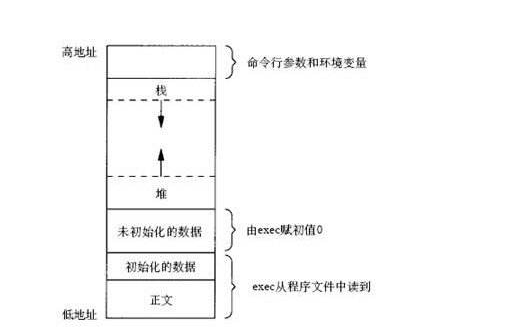
JAVA的堆和棧介紹和內(nèi)存機(jī)制中堆和棧的區(qū)別及變量在內(nèi)存中的分配

什么是棧?數(shù)據(jù)結(jié)構(gòu)中棧如何實(shí)現(xiàn)
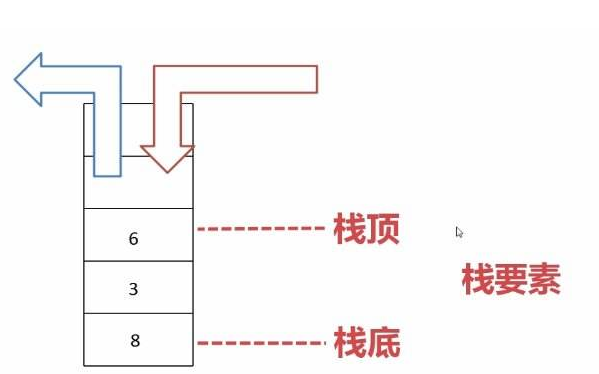
如何解決數(shù)據(jù)結(jié)構(gòu)設(shè)計(jì)最大頻率棧問(wèn)題?
PLC編程實(shí)現(xiàn)堆棧功能

PLC實(shí)現(xiàn)入棧出棧功能

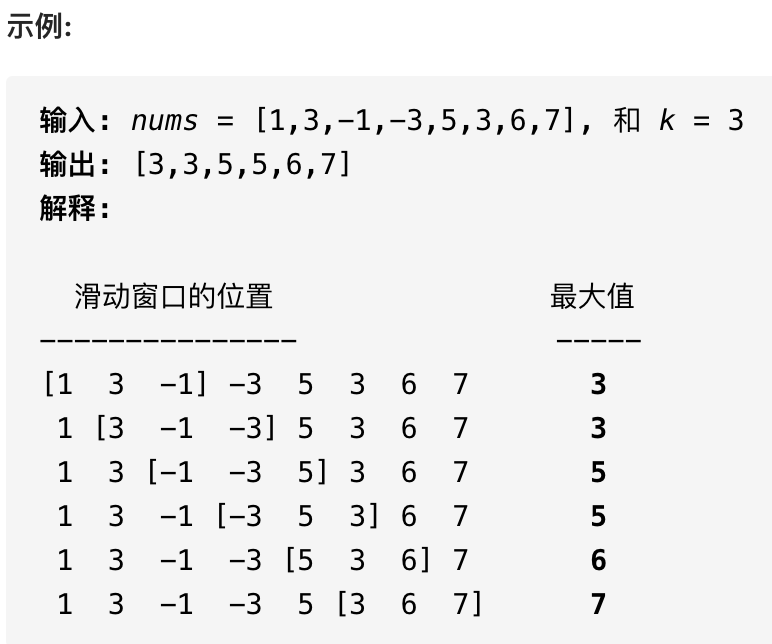
數(shù)據(jù)結(jié)構(gòu)解決滑動(dòng)窗口問(wèn)題





 數(shù)據(jù)結(jié)構(gòu)中堆棧出棧序列問(wèn)題解析
數(shù)據(jù)結(jié)構(gòu)中堆棧出棧序列問(wèn)題解析










評(píng)論