摘要

Σ-Δ模數轉換器是從脈寬調制器類積分型ADC演變而來的，其模擬部分相對容易實現、數字部分則比較靈活。隨著技術的發展，Σ-ΔADC基本原理已結合不同量化器形成了有意義的變種。本應用札記回顧了與Σ-ΔADC相關的重要概念與拓展：過采樣、（量化）噪聲整形、（量化）噪聲調制、數值化、濾波抽取，以及殘量累積和局部精細量化（Zoom）等變種。

目錄

1 Σ-Δ ADC概述... 2

2 過采樣量化噪聲整形和量化噪聲調制... 4

2.1 量化噪聲與ADC的分辨率... 4

2.2 過采樣量化噪聲整形與ADC的分辨率... 5

2.3 量化噪聲調制... 6

2.4 改善量化噪聲抑制收斂速度以及階數的概念... 8

3 抽取和濾波... 9

4 改進和變種... 10

4.1 局部放大（Zoom）Σ-Δ型ADC. 10

4.2 殘量繼承電容DAC SAR預量化Σ-Δ型ADC[4][5][6] 11

參考資料... 11

?

以1作為量化門限時，0.7被量化為0；無論多少次采樣0.7保持被量化為0。只有1這一個量化臺階的Σ-Δ型ADC經過反復量化可以得到0.7；Σ-Δ量化的基本原理是從多次量化中抽取其統計分布中心，結合其它量化方案可以加快誤差收斂速度和提高量化分辨率。關于Σ-Δ型ADC的文獻最早出現于1962年[1]，早期的原理討論淹沒在了深化研究之下。本札記試圖鉤沉這些早期原理討論，為理解Σ-Δ型ADC做入門鋪墊。

1 Σ-Δ ADC概述

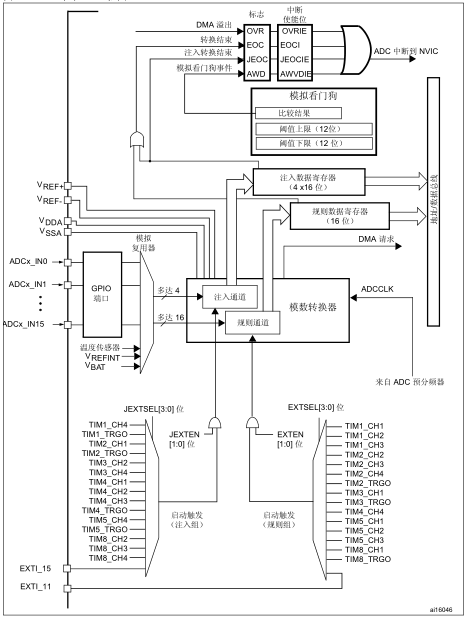
圖 1是介紹Σ-Δ型ADC工作原理時常見的頂層框圖，圖中將Σ-Δ型ADC表達為Σ-Δ調制器和數值抽取濾波器兩個環節。該圖表達了Σ-Δ型ADC的兩個關鍵特征，其一是有一個調制過程在一個時間段內使調制量與模擬輸入相互作用，其二是以k×fs的過采樣速率獲取速率為fs量化輸出。采樣孔徑[1]指量化輸出反映的模擬輸入片段的整體效果。就Σ-Δ型ADC而言，對調制狀態流采樣需要持續時間、濾波器需要狀態建立時間，表現為采樣孔徑大、輸出延遲大。采樣孔徑的大小和輸出延遲表現為量化過程的幅頻特性和瞬態響應特性。

圖 1 Σ-Δ型ADC頂層框圖

圖 1是概念性框圖，圖 2則是具體以脈寬調制器為Σ-Δ調制器的Σ-Δ型ADC的功能框圖，方便更具體地說明其各個局部的功能。該電路中調制器的狀態流為脈寬調制器的占空比信號，調制量流是受占空比信號控制的、相對于中間值電壓VCOM的±VREF偏移電壓。VX的范圍限制在VCOM±VREF范圍內。

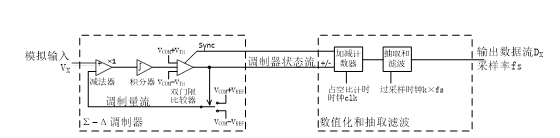
圖 2 具體基于脈寬調制器的Σ-Δ型ADC的功能框圖

當調制量流為VCOM-VREF時，減法器輸出為正，積分器輸出逐漸增大。直到積分器的輸出超過上閾值VCOM+VTH，雙門限比較器輸出翻轉、將調制量流輸出切換為VCOM+VREF。由于VX幅度在VCOM±VREF范圍內，上述切換后積分器輸出逐漸變低。積分器輸出變低最后會超出下閾值VCOM-VTH，雙門限比較器輸出翻轉、將調制量流輸出切換為VCOM-VREF方波幅度流。當VX=VCOM時，調制器狀態流輸出占空比D=1:1；當VX與VCOM不同時，占空比D反映VX偏離VCOM的程度，即D=0.5 + (VX-VCOM)/(2×VREF)。或者，在中心值為0時，VX=2×(D-0.5)×VREF，即VX決定了占空比偏離1:1的程度。調制器的狀態流是對積分器輸出的量化結果，該結果影響調制量流，但不是對VX的量化。VX通過調制器反映為調制器狀態流的占空比，這個占空比由圖中加減計數器讀取，計數器的值為VX的量化值。在一個周期內占空比計數器的量化誤差反映為調制器狀態翻轉時間與計時時鐘clk對齊的偏差，即可能存在一個時鐘周期的偏差。重復多個周期，總計數時間不斷增大，這一個周期的量化誤差占比不斷減小。這種通過多個周期不斷累積獲得精確占空比的過程即抽取[2]過程。由于VX是變化的，過長的累積過程會掩蓋掉VX的變化，上述累積需要利用具備一定時間常數的數值濾波器實現，即抽取和濾波是同時由濾波單元實現的。

上述原理介紹中沒有提及圖 2中Sync信號的功能，該功能與Σ-Δ型ADC設計方案的演化相關。圖 2電路是典型的早期雛形積分型ADC；如果Δ代表差值、Σ代表積分，則此雛形電路應為Δ-Σ型ADC（部分文獻[1]仍采用Δ-Σ的命名）。Sync信號的引入取代了早期Σ-Δ型ADC方案中的加擾電路（dither），利用它在積分環節引入了一個殘差，亦可用Δ表達。引入Sync信號后，該類型的ADC則名副其實地稱為Σ-Δ型ADC了。上述殘差與加擾電路的功能一致，用來保證量化誤差能在一定范圍的量化臺階內均勻分布。這個保證量化誤差均勻分布的功能即（量化）誤差調制，將在下文2.3中進行詳細討論。

Σ-Δ型ADC本質上或者底層原理是利用多次采樣取平均將量化誤差對消。無論是圖 1還是圖 2，用來分析量化噪聲的調制如何改善信噪比都太過具象，通常利用圖 3所示的一般模型做理論分析。該模型中，帶有量化噪聲的量化結果被送回到輸入與輸入模擬量相減合并到下次量化中；如果每次量化作為一個迭代周期，則每次迭代量化誤差的極性是翻轉的。如果量化誤差是完全隨機的，即出現正隨機誤差和負隨機誤差的幾率一致，則經過充分迭代后，量化誤差反復加減后會趨于零。圖 3中輸入到ADC的是VH，但ADC的輸出并不是VH，而是根據一段時間內VH的變化得到的VX量化值DX；對VX的量化過程是從對VH量化提取得到的。直觀的解釋是重復對VX做多次采樣取其平均值，有正有負的量化誤差被平均過程減小了。

圖 3 分析Σ-Δ型ADC中量化噪聲改善影響的一般結構框圖

Σ-Δ型ADC的三個關鍵特征分別是，過采樣過程將量化噪聲推到高頻、在大量數據中抽取出量化值及濾波、以及保證量化噪聲的平穩和均勻分布。

2 過采樣量化噪聲整形和量化噪聲調制

借助于奈奎斯特采樣的分析方法從信息提取角度可以導出過采樣過程如何提高量化精度的一般性解釋。首先，仍需要假設量化噪聲是平穩和均布的，以及過采樣數據處理過程不引起信息損失，即僅考慮過采樣時的量化誤差。以下將解釋如何從信息提取的角度評估量化噪聲與ADC位長的關系以及將量化噪聲調制在量化臺階內的實施例。

2.1 量化噪聲與ADC的分辨率

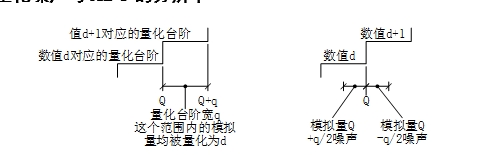
圖 4 理解量化臺階和量化噪聲的示意圖

參考圖 4左圖，不局限于Σ-Δ型ADC，量化臺階指對應相鄰兩個量化值的模擬量范圍，在這個范圍內模擬輸入都被量化為同一個數值，即圖中的d。記d臨界變化的模擬量是Q，相鄰數值d+1臨界變化對應模擬量為Q+q，則數值增量1對應的模擬量增量q即量化臺階。對于線性量化過程，這個臺階即最小量化權值位LSB（less-significant bit）對應的模擬量范圍。這種將模擬量量化為數值時，因數值表達的不連續性導致的誤差即量化誤差。將量化誤差看作噪聲影響時其效果相當于在模擬量上疊加了幅度在-q~0范圍內的噪聲。考慮這個噪聲是均勻分布的，則平均值為-q/2，即圖 4左圖所表達的量化誤差從統計結果看同時引起統計零點出現-q/2的漂移。這個漂移可在數字域或模擬域移除，從而可以將量化噪聲反映為如圖 4右圖所示的-q/2~+q/2的噪聲，即量化結果d對應較Q低的實際輸入量疊加了同相噪聲或較Q高的實際輸入疊加了反相噪聲。此時在-q/2~q/2范圍均布的噪聲的均值為0（在-q/2~0范圍內均值為-q/4，在0~q/2范圍內均值為q/4），方差密度或噪聲密度為σ= ，式中A為幅度，σ為能量或方差。有限次量化時，n次量化噪聲平均幅度在正和負兩個部分分別為正和負(q/4)/(n1/2)[3]。相對于單次量化時在兩側的均值q/4，隨著量化次數的增加，均值以1/n1/2速度縮小。由于噪聲能量總是正值，量化次數不改變平均到每次的噪聲能量，而只是改變其短期統計偏差與長期統計偏差的偏離程度。

長期且平穩時，信號能量密度與噪聲能量密度為1:1的相對關系用來表述一個信息表達系統的極限能力；量化系統極限有效動態范圍以信號/量化噪聲比SINAD表達為10×lg(Ps/Pn)（dB），其中Ps為信號能量密度，Pn為噪聲能量密度。對于N位ADC，其不失真地采樣一個正弦信號的幅度為2N×q/2，其能量為22×N×q2/8，前述極限有效動態范圍為10×lg[(22×N×q2/8)/(q2/12)]，即SINAD=1.76+6.02×N。由此可看出，位長N與信噪比的正比關系。從另一個角度看SINAD的表達，如果一個量化系統在原始采集到的數據基礎上的后續處理過程中數字表達不受位長限制，降低Pn可獲得更高的SINAD。即，如果平均過程可以降低量化噪聲平均幅度，則可借助平均過程獲得更高的SINAD。

2.2 過采樣量化噪聲整形與ADC的分辨率

2.1中已說明重復n次采樣和量化時平穩和均布的量化噪聲以1/n1/2的比例減小，以及如果處理過程不受位長影響，量化噪聲的減小相當于有效位長增加。將其中SINAD的公式改寫為N=(SINAD-1.76)/6.02=[10lg(Ps/Pn)-1.76]/6.02，帶入n增加時量化噪聲幅度減小1/n1/2的比例關系后，得到n每增加一倍，等效位數增加0.5位的關系[4]。需要注意，此處的量化噪聲能量并不是多次量化的平均量化噪聲能量，而是從平均量化噪聲幅度折算得到的等效值。多次采樣取平均只是多種數據處理方式之一，從量化噪聲能量變化的角度可導出過采樣改善ADC分辨率的一般性關系。

當以fs為采樣速率對模擬信號采樣時，如圖 5所示，帶寬為fa的模擬信號及其鏡像部分經采樣后被搬移到以fs頻率的兩側。奈奎斯特采樣定律指出最低限度地識別信號頻譜的極限情況出現在fs=2×fa時；當fs＜2×fa時，fa頻譜中高于fs/2的部分出現交錯，致使該部分的功率高于實際信號功率，從而導致誤判。在臨界情況下，即fs=2×fa時，采樣過程將量化噪聲調制到了帶寬為fs的采樣頻譜中，這時量化噪聲的影響最大。

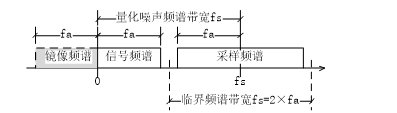
圖 5 采樣對模擬信號頻譜的搬移

量化噪聲可能出現的最高頻率即采樣頻率fs，作為白噪聲時在0頻率到fs間均布。當信號帶寬小于fs時，則只有fa/fs比例的量化噪聲被調制入采樣頻譜。記fa/fs=1/n，則量化噪聲可以調制到采樣頻譜中的部分為1/n。將這個關系帶入公式N=[10lg(Ps/Pn)-1.76]/6.02中，即得到只有部分量化噪聲進入采樣頻譜時ADC分辨率改善的一般關系[5]。

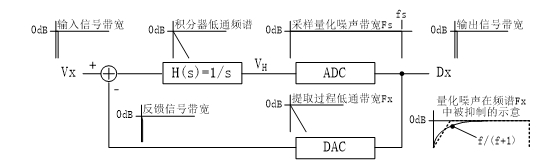
圖 6 增加了頻譜示意的抽象結構框圖

圖 6在圖 3所示的抽象結構基礎上增加了信號帶寬和傳遞函數帶寬的示意，明確了以積分器作為簡潔的模擬低通濾波器限制量化噪聲頻譜的一般性特征，沒有明確ADC的形式和DAC的形式及其反饋延時關系。分析上圖，傳遞方程為DX = (VX-DX)×H(s) + qN，在低頻范圍不考慮相移影響，上述方程可簡化為DX = (VX-DX)/f + qN，可推導出DX = VX/(f + 1) + qN×f/(f + 1)，該導出式顯現對于極點為零的積分器型濾波器，當f接近零時，量化噪聲的影響也接近零。由此可見，對量化噪聲的抑制是由濾波器H(s)、對VH量化和從中提取對窄帶的VX量化結果的（濾波）過程中實現的。

以上即量化噪聲整形的一般性概念，利用過采樣使量化噪聲分布在很大帶寬內，然后只保留有限帶寬內的量化噪聲，從而取得比過量化量化器高的有效位長。過采樣和量化噪聲整形的概念并不局限于低通方式，也包括對高頻窄帶信號（相對于帶通帶寬的）過采樣和利用帶通濾波實現噪聲整形的情形。

2.3 量化噪聲調制

量化噪聲調制是使量化噪聲呈現白噪聲或者接近白噪聲的過程。量化器本身不能保證多次量化過程中量化噪聲是均勻分布的。例如當模擬量在一個量化臺階內保持穩定時，無論是多少次采樣所采集的數據是個確定值，則無論如何抽取和濾波，都不會改變量化噪聲的幅度，從而無法提高有效位長。圖 3中利用DAC將量化結果反饋到前端與輸入信號相減的過程在每次迭代時翻轉量化誤差極性可以加快量化誤差的收斂速度，但仍不能使處于一個量化臺階中的穩定輸入引起不同輸出，因此也無法使量化誤差均布。

Σ-Δ型ADC的早期設計中曾使用主動加入擾動的方式使多次量化的結果在若干位間以輸入模擬量為中心對稱分布。利用加入擾動的產品實例可見MAX110/111[2]（ADI公司產品），其利用一個擾動產生單元（dither generator）產生一個對稱分布的準白噪聲使對穩定輸入信號的量化結果出現在不同編碼上；量化結果的統計分布中心即加擾后的模擬信號的中心，而該統計中心位置精度由統計樣本規模決定、不受量化器精度限制。后期設計中很少使用加擾，但加擾方案中由多個量化臺階上的樣本數決定統計分布中心的精髓得以延續；利用取多個臺階的平均值改善臺階幅度偏差。

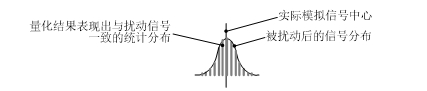
圖 7 利用加擾使多次量化結果以輸入量為中心分布的示意

圖 2中的Sync信號利用比較器翻轉時間與一個穩定的計數時鐘的偏差來產生一個殘量（即文獻[3]第16、17頁提到的線性時間變量）。這個殘量的幅度在一個Sync時鐘間隔內均勻分布，完全符合Σ-Δ型ADC的需要。帶有同步信號的比較器，即鎖存比較器，在Sync信號前沿瞬時將輸入接入一個雙穩態觸發器；無論輸入幅度差是多少，這個雙穩態觸發器一定會產生唯一的邏輯狀態，是一種高增益比較器。鎖存比較器只在Sync信號前沿瞬時檢查獲取輸入幅度信息。如果過閾值的臨界狀態出現在兩個Sync信號前沿之間，臨界時間與比較器輸出之間出現延時；在這段延時期間積分器保持原來的狀態，輸出在過閾值后繼續變化。

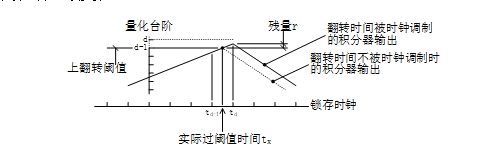
圖 8 翻轉時間被時鐘調制產生殘量的示意

圖 8說明了上述延時如何產生在一個量化臺階內隨機均布的殘量，以及這個殘量帶入下一個積分過程的情形。如圖所示，以過上翻轉閾值為例，實際過閾值時間發生在tx時刻，但直到td時刻鎖存比較器才檢查積分器輸出。從過閾值到鎖存比較器輸出翻轉、改變積分器的變化方向，積分器輸出仍沿著之前的方向變化并產生了一個與td-tx時間有關的殘量r。這個殘量r使得積分器在下一個方向上的變化的起點偏離了量化臺階的端點，是對其計時過程的擾動。考慮tx與時鐘無關，同時在td-1~td的時間范圍內積分器輸出的變化不大，則殘量r在一個量化臺階內均布。對于經常采用的一位量化器而言，殘量r是積分器輸出超出上下翻轉閾值的部分。對于圖 2所示脈寬計數結構的電路來講，殘量r則是均勻分布在d-1和d之間的隨機擾動。除擾動加入方式不同外，圖 2電路與產品實例MAX110/111一樣，單次量化器是多位精度的脈寬計時器；這個單次量化器的分辨率或位數對應積分器一個完整充放周期的計時。

Σ-Δ型ADC的關鍵特征是在單次采樣量化后的數據處理，這是一種廣義的積分過程，即需要某種方式讓多次量化的結果關聯起來；這種情況下單次量化被稱為預量化，后續的處理仍被稱作抽取和濾波過程。其中單次量化器則不局限于積分變換器，例如可以采用基于電荷平衡的逐次逼近型的SAR ADC。電荷平衡SAR ADC可借助其權電容將上次變換所剩余的殘量帶入下次變換采樣中，實現量化噪聲調制[4]。

量化噪聲調制過程同時作用到其它類型由量化器引入的低頻噪聲。部分殘量由量化器的低頻噪聲引起，這部分沒有計算到積分時間內的殘量在下一個方向的積分過程中以反向的形式導致積分的起點向延長積分時間的方向移動。在接續的兩個積分過程中，量化器引入的噪聲分別表現為正和負的影響，相當于利用以積分時間為周期的±1極性對稱方波進行了調制。考慮其作用的一致性，進一步的討論中不必區分量化噪聲和其它類型由量化器引入的噪聲。

2.4 改善量化噪聲抑制收斂速度以及階數的概念

利用快速預量化可直觀和直接地改善收斂速度，大多改進出現在積分調制器和抽取濾波部分（自從1962年這個分類被提出后，大量研究和產品實踐都是圍繞調制器和抽取濾波展開的[1]）。本小節試圖提供有助于理解這些創造的一般概念，而不是嘗試概述。

將圖 3表達為以固定節拍迭代的離散過程，見圖 9。類似地，圖 9只是表達數據提取部分是對之前輸入的量化、僅將量化誤差反向后送回積分的概念，而忽略了其具體實現的復雜性。這個過程的z域表達為D(z) =z-1×X(z) + (1 – z-1)×Q(z)；其中從X(z)到D(z)以1:1增益傳遞，Q(z)為量化誤差序列，z-1代表一個延遲節拍，(1 – z-1)為積分器（與1/s或f/(f + 1)對應的）在零頻率上的陷波函數。其收斂速度慢表現在由f/(f+1)反映的關系上，只有當fs>> fa時才能對量化誤差的有效抑制。

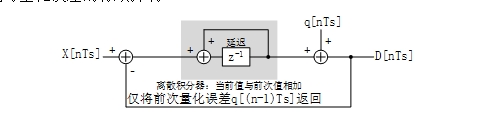
圖 9 以離散過程表達的Σ-Δ型ADC的結構

直觀的改善辦法是嘗試堆疊調制器積分節，使傳遞函數與積分器相關的部分連續延遲-相乘的關系表達為D(z) =z-1×X(z) + (1 – z-1)L×Q(z)；其中L為級聯次數。以三階級聯為例，相應的傳遞模型如圖 10所示；其中系數a1~a3表示在累積延時-積分時的傳遞增益需要控制。這個級聯次數L即所謂Σ-Δ調制器的階數。(1 – z-1)L被稱為量化噪聲整形函數，圖 11是其在0~0.5fs頻率范圍的模值。

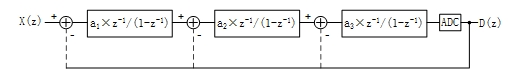
圖 10 對量化誤差做三階級聯積分的模型

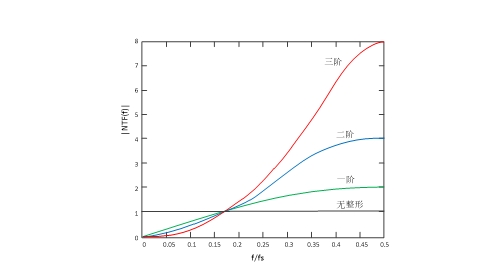
圖 11 整形函數(1-z-1)L在0~0.5fs頻率范圍的模值

(1 – z-1)L的模值為[2×sin(π×f/fs)]L，是2×fs的周期函數。其在零頻率附近的斜率變化與L階冪函數一致，使得L增大時在低頻部分殘余的量化噪聲快速下降。每增加一次級聯相應增加一個延時單位，同時在較高頻率上的傳遞增益快速增加（在f = fs/2處增益為2L）。使用高階結構時需要插入濾波器控制傳遞增益或者采用高位長的預量化器來減小量化噪聲的相對幅度以防止出現自激。

3 抽取和濾波

過采樣產生的大量數據需要在第一時間壓縮和提取有效部分，以便減小后續需要處理的數據量。這部分處理即抽取（decimation）或退過采樣（down-sample）。具體實施均采用對一段時間內采集的數據連續加和獲取平均值的方式來實現。連續加和即離散積分的過程，不需要中間數據寄存器即可完成。如果一個時間片完成后再啟動下一個時間片，則只有完成一次整時間片的加和才能看到數據的變化，處理延時長并且對變化不能快速響應。普遍利用滑動平均（moving average or sliding average）在平均樣本數和快速響應間折中。M階的滑動平均需要存儲M個中間數據，每輸入一個新數據同時放棄一個最老的數據，然后以新的M個數求取平均值。滑動平均僅需要加減操作和桶形結構先入先出寄存器組即可實現。當過采樣比較大時可能需要采樣分片加和級聯多次滑動平均的方式減少電路規模，這時的每個處理節稱為分段預采樣。分段預采樣的離散轉移關系為 ，傳輸函數z域表達為(1-z-M)/[M×(1-z-1)]。當M為1對應分片加和的情況，幅頻響應為SINC函數；M階滑動平均相當于按M次倍頻嵌套相乘多次SINC函數，可以改善最低頻的SINC在低頻部分的平坦度和陷波頻率點附近的衰減速度。這種多次嵌套SINC的幅頻圖上可見在最大滑動區間對應的頻率處出現一連串陷波頻率點，因其曲線形狀也被稱為梳狀濾波器[1]。

經過梳狀濾波器后數據流速率得以降低，而后接入濾波器可以減小濾波電路的規模。對于窄帶應用的輸入頻率相對于實際需要的帶寬仍然可能過高，還是需要利用級聯方式將濾波器分節實現，以便減小電路規模。

4 改進和變種

使量化噪聲均布，然后利用過采樣和抽取過程減小量化噪聲的基本原理配合多種類型ADC實現折中的性能改善。以下介紹常見的局部放大（Zoom）Σ-Δ型ADC和基于電荷平衡的殘量繼承電容DAC SAR預量化Σ-Δ型ADC。

4.1 局部放大（Zoom）Σ-Δ型ADC

利用其它高速或中速ADC，例如采用SAR ADC，快速預量化輸入模擬量后，將預量化結果快速帶入抽取和濾波邏輯，以預量化值為起點可以加快向更精確量化結果的收斂速度。如果只是用來預置收斂過程的起點，Σ-Δ調制器的輸出擺幅不變，調制器部分的時間預算不會降低。

將預量化結果利用DAC還原為模擬量，將輸入減掉還原模擬量得到一個差值，將此差值送入一個Σ-Δ型ADC則可以使Σ-Δ調制器只作用在差值所對應的局部。此實現方式的ADC即局部放大（Zoom）Σ-Δ型ADC，原理圖見圖 12。

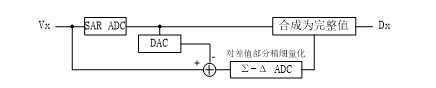
圖 12 局部放大（Zoom）Σ-Δ型ADC的原理

局部放大型ADC適合要求對局部做高精度解析的應用，例如在大尺度測量時獲取以節距為參考的定位，以及測量圍繞某個中心值的弛豫過程。在這些應用中節距或者中心值的精度要求與圍繞節距和中心值的變化的精細要求不同，需要局部放大和量化。從動態范圍角度看，局部放大的獲益局限于其Σ-Δ ADC所處理的局部；全局的量化特性受預量化ADC和還原DAC的制約。局部放大型ADC可以快速輸出預量化值，用于節距定位，也能以慢速Σ-Δ型ADC的方式獲得精細解析結果。

4.2 殘量繼承電容DAC SAR預量化Σ-Δ型ADC[4][5][6]

利用電荷平衡型的電容DAC做SAR型ADC時，完成逐次逼近的節拍后、權電容陣列上會殘留一個或正或負的電壓。這個電壓對應一個電荷殘量，如果將這個殘量帶入下次量化，則相當于實現了量化噪聲調制。相對于圖 2所示或產品例MAX110/111的脈寬計數預量化和量化噪聲調制，殘量繼承可以快速實現殘量調制和預量化，其整體電路結構也比前述局部放大型的結構緊湊。在這種結構方案中，預量化和殘量調制是同一個過程的兩個結果，是最快的噪聲調制方式。對一次預量化而言，殘量在一個量化臺階內是均布的；從多次量化間逐次繼承來看，該殘量的累積影響了下次變換結果，即在SAR ADC結果中包含了一個積分ADC作用。當除量化噪聲外的其它噪聲影響不大時，積分型量化變換的分辨率與積分時間成正比。以過采樣倍數n來表達，殘量繼承預量化對位長改善能力在n1/2~n之間，高于單純以隨機噪聲所做的測算。

參考圖 12所示的原理，SAR量化結束后的殘量即該次采樣與該次量化還原值之間的差值。與局部放大型(Zoom)相比，每次量化的還原值可能是不同的（因量化噪聲之外的擾動）。這導致預量化結果的變動，使預量化的微分非線性影響進入差值。這個影響同樣會經過抽取濾波過程被均化和減小。進一步地，如果有意隨機地提前結束逐次逼近，可將殘值擴大到多個位，進而利用抽取濾波在多個位之間均化其微分非線性的影響。

參考資料

[1] Philips E. Allen, Douglas R. Holberg. CMOS Analog Circuit Design[M]. 2nd ed. Oxford University Press, Inc., U.S.A., 2002.

[2] Analog Devices, Inc. MAX110/MAX111 Data Sheet[EB/OL]. (1998-11). https://www.analog.com/media/cn/technical-documentation/data-sheets/1018.pdf.

[3] Shanthi Pavan, Richard Shreier, Gabor C. Temes, Understanding Delta-sigma Data Converters[M]. 2nd ed. Wiley-IEEE Press，2017.

[4] 雷鑑銘，劉佳明，馬常樂，譚磊，白瑋. 一種基于殘量累加電荷的逐次逼近型數模轉換器：202210664014.8[P]. 2022-06-13.

[5] 譚磊. 一種模數轉換器及其操作方法：202111617749.7[P]. 2021-12-27.

[6] 白瑋，譚磊，于翔，謝程益. 模數轉換器：202111597874.6[P]. 2021-12-24.

修訂記錄

重要聲明

SGMICRO保留更改電路設計、產品規格和產品描述的權利，恕不另行通知。

本文檔內容僅供參考。本文檔中的所有陳述、信息和建議不構成任何承諾。對于本文檔中可能出現的錯誤，以及因本文檔提供的信息和使用本文檔而造成的任何附帶或間接損失，本公司不作任何明示或暗示的陳述和保證。

此文檔未授予任何知識產權許可。除了SGMICRO在其產品的銷售條款和條件中聲明的責任外，本公司概不承擔任何其他責任。