大數據的挑戰與隨機機器學習算法
大小:0.6 MB 人氣: 2017-10-13 需要積分:1
數據在不斷地增長,數據量很大的時候是非常重要的一件事情,因為數據只有到了一定的程度的量才會發生質的變化,有一個例子是Matrix Completion(矩陣補全),就是給你一個表,有一部分的數據你知道,有一部分數據你不知道,沒有辦法拆出來,這個東西就是矩陣補全。矩陣補全非常重要,幾乎所有的機器學習的問題都可以表示成矩陣補全的問題,這里顯示的聚類,也可以看成矩陣補全。
矩陣補全非常有意思的結果是怎樣的?我們這邊的橫軸是數據量,考慮在矩陣里能夠看到的數據量,縱軸是恢復誤差,拆出來的結果和真實結果的誤差,肯定是數據量越多拆的誤差越高,當數據低于一定程度的時候,這可以是非常顯示的刻劃出來,在數據小于一定量的時候,不管怎么做總是拆的很糟糕,幾乎沒有太大的區別。只有當你的數據大于一定量的時候,突然你可以拆的非常準,如果按原來的說法,在一個的情況下,你可以拆的很完美,沒有任何的錯誤。所以我們說大數據,只有當數據到一定的程度的時候,有些事情才是可能的,當你的數據小于這個的時候,不管你怎么做都永遠不可能。
大數據帶來的困難我們大家一直在談大數據的挑戰,來到阿里之前我沒有意識到,來了之后覺得這個事情真的是big deal。做任何統計是最重要的一件事情,比如這里非常基礎、簡單的任務——矩陣平均,即便只是簡簡單單地做大數據下的平均,也是一個big deal,每一個矩陣都是很大(1Bx1M)。在應用里頭,這個矩陣記錄了每個人對每個商品行為的矩陣,這個矩陣是非常大的,但每天記錄下的矩陣是很稀疏的,雖然說你有幾百萬幾千萬的商品,但通常每個人只有在很少量的商品上的行為,你希望把這些矩陣加起來,平均表達出在一個人在很長的周期內的行為是什么樣的,但是一個disaster就發生了,如果矩陣做一個平均、求和,這個矩陣會變成一個death的矩陣,如果不做任何smart commutation,這個事情實際上是非常昂貴的,而且存儲也是昂貴的。我在阿里的第一件事情,就是我能不能做一個這樣的平均,我雖然不能算出確切結果,但有沒有辦法說我可以算出大概結果?最后一個很簡單的辦法,就是用一個隨機算法做這個事情。
隨機算法的好處所謂的機器學習問題(Learning Problem),一般的機器學習問題會寫成這樣的形式,考慮有一堆訓練樣本,有一個叫Lost Function,用來比較預測和現實的差別,并分析這些差別。通常,Learning Problem就是找到一個解,確認這個解能夠給出正確的預測和訓練樣本,通常可以把它變成一個優化問題來做。

解決該問題的主要挑戰在于兩個方面:一個方面是樣本數量很大(1Bx1M),還有一個問題是維度非常高,通常來講都是億級,要解決的不會是一個簡單的問題。一個成熟的解決方案就是隨機算法。相信很多人都有意無意地使用到隨機算法,比如用LR、SGD。
隨機算法有兩個好處:
隨機算法的Efficient,包括兩個方面,第一個方面是即使針對大規模樣本也不需要多次掃描數據,另一個方面,如果是非常高維的數據,一個簡單的辦法是可以使用隨機投影(Random Projection)來降低維度,這樣可以不用直接解決高維問題;隨機算法的Effective,就是它通常有最小化泛化誤差 (Generalization Error) ,不僅僅是計算簡化,同時也可以提供很強的保證。
隨機算法的挑戰(以隨機投影為例)
隨機算法很好,但是總體來講,隨機算法還是有很多的局限的,我的演講用一個很簡單的隨機投影問題來討論,來看一下隨機算法的問題在哪里。
隨機投影是一種非常簡單的方法,而且應用廣泛。一個高維矩陣X,long long vector,處理起來很麻煩,計算量很大,而且可以證明優化收斂速度跟維度是有關系的。一個簡單的做法,針對非常長的vector,乘上一個非常fat的隨機矩陣S,乘完以后得到一個很短vector的X point,很低維度的表示,就把這個X point變成我的數據,用低維的數據來優化問題,在低維空間學習。這個好的解是一個很矮的vector,我還要回到原來的空間上去,把原來的矩陣轉置一下,又變成一個很長的vector,就變成最后的解。幾乎所有的random projection都可以這么做:把一個(很長的)vector用一個隨機矩陣變成一個很短很短的vector,算出一個解來,再把矩陣轉置,把最優解一乘就可以了。這是一個非常簡單的算法,是使用廣泛,而且有無限多的paper分析這個東西有沒有效。幾乎所有的paper都告訴你這個東西很有效,也可以證明它很有效,但是我覺得所有的paper都很理想化,通常會假設原來的問題是一個很容易解的問題,可以證明所有的東西都是對的,但不幸的是,如果你的問題是比較難分類的問題,它告訴你的所有story都是假的。所以這其中隱藏了一個非常有趣的幾何泛函的問題,一百多年前就已經被well study。也就是說,這個W star是真正的最優解,把所有的高維數據放進去讓機器run獲得的最優解,而所有W star cute就是剛才說的用隨機投影的算法降維得到的解,你可以證明這兩個解通常會有非常大的差別,這個差別跟原來的vector應該是一個數量級的。
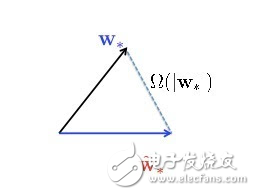
所以說run隨機投影的算法拿到的解,跟原來的解有很大的差別。這是不是因為我描述了一個非常特定的過程,這個中間的過程造成這個解不好,所以是不是嘗試一下變化一個問題就有機會拿到更好的解呢?非常不幸地告訴你,這是不可能的,這也就是我說的Impossibility Theorem,可以證明這個事情不管怎么玩,只要做隨機投影,不管你怎么去解這個w star cute,這兩個解永遠是差別很大,這和怎么解的問題都沒有半毛錢關系。而且非常奇怪這個東西一百多年前都知道了,不知道為什么沒有人提出來。但是對我來說這個事情很有意思,我能不能做其他的事情,稍微加一點限制,就能讓我這個疏密的問題解掉?
對偶隨機投影的優化
這是五年前讓我很感興趣的一個問題,我們創造了一個對偶隨機投影 (Dual Random Projection),非常簡單、非常神奇,把隨機投影得到的w star cute這個解塞到每一個Lost Function里去,然后去求一個導數,這里稱為alpha i,最后的解是用每一個training instance和alpha i對應,所以你需要做的,不是直接采用隨機投影得到的解,而是用隨機投影的解去算它的對偶變量,用對偶變量去win每一個training instance。
非常好我支持^.^
(0) 0%
不好我反對
(0) 0%
