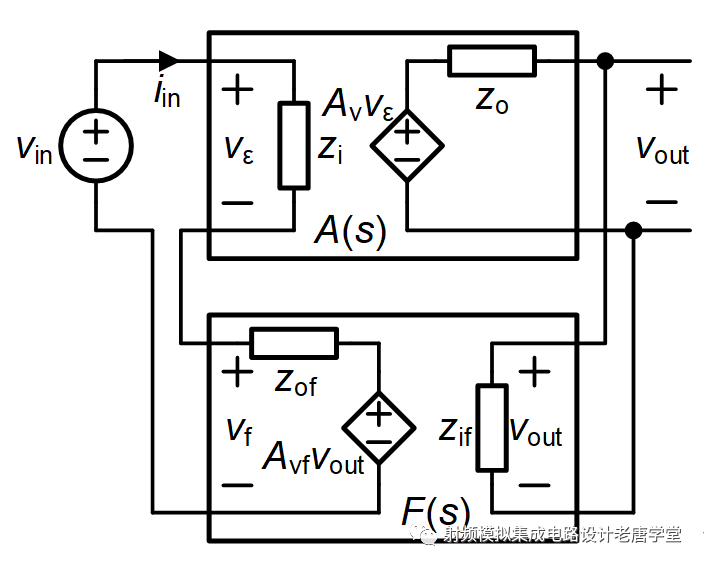
無論拓撲結構如何,閉回路(close-loop)增益都是通用形式:
其中A ideal是理想極限a ε →∞時的閉回路增益,a ε是開回路增益,T=a ε /A ideal是回路增益。盡管運算放大器是電壓輸入/電壓輸出(VV)元件,但它可以配置為四種拓撲結構中的任何一種。現在我們來討論II拓撲結構,并由此引出負回饋的其他細節。電流放大器圖2的回饋拓撲結構通常稱為并聯-串聯型,其中具有開回路電壓增益a v的運算放大器被配置為電流放大,其增益可表示為A=i O /i I (除了a v<∞的情況,該運算放大器假定是理想的。另外,為簡單起見,我們假設負載短路,這是電流輸出元件最簡單的負載類型,就像開路是電壓輸出元件最簡單的負載一樣)。
圖2:使用運算放大器作為電流放大器,或II轉換器。要得到A ideal,參考圖3a,我們有:
消除v O,整理得到:
參考圖3b,可以看到沿回路傳輸的訊號v D首先被a v放大,然后通過LD和R 2完整地返回到運算放大器的反相輸入端,因此回路增益僅為T=a v。我們是否可以應用公式(1)得到下面的公式?
讓我們透過PSpice軟體工具來看一些特殊情況,例如R 1 =R 2 =10kΩ和a v =10V/V。然后,公式(3)得出A=2/(1+1/10)=1.818A/A。然而,PSpice卻得出1.909A/A,雖然差別不大,但對于這樣簡單的電路來說絕對是不能接受的。在圖3c中a v →0的情況下甚至出現更大的差異。藉由檢查發現,i O =i I,因此A=i O /i I =1A/A,而公式(3)預測A=2a v /(a v +1)=2x0/(0+1)= 0A/A!
圖3:獲得(a)A ideal;(b)回路增益T; (c)饋通增益a ft的電路。有什么問題?公式(3)的問題在于它試圖使II轉換器符合圖1的電路圖,它假設訊號單向傳輸,即透過放大器正向傳輸,以及透過回饋網路反向傳輸,如圖中的箭頭圖形所示。然而,仔細審視II轉換器就會發現,回饋網路是雙向的,如圖3c所示,在將v N =v O /(1+R 2 /R 1 )回饋回運算放大器的反相輸入時,網路也將i I前饋到負載,繞開了運算放大器。這時,饋通增益為a ft =1A/A。我們該如何考慮這種雙向性?電路很簡單,我們可以直接分析它(參考文后的附錄)。確切的結果是:
這與公式(3)不完全相同。但是,我們可以輕松地將公式(4)重新表達為:
其中最后一項確實考慮了訊號饋通。在我們的范例中(R 1 =R 2 =10kΩ及a v =10V/V),公式(5)得出A=1.818+1/11=1.909A/A,本來就應該這樣。透過PSpice查看各種增益還是很直觀的。圖4a的電路采用了一個直流增益為10V/V、增益頻寬積GBP為10MHz的運算放大器(沒錯,這里特意采用低于標準的運算放大器,以更充分顯示由饋通產生的影響)。從圖4b的跡線(trace)可以看出,只要a v (跡線#1)足夠高,饋通分量(跡線#3)可以忽略不計。然而,a v隨著頻率滾降,饋通變得越來越相關,最終占據主導地位。因此在高頻下,跡線#4與跡線#3匯合,使得A→a ft。
圖4:(a)用于模擬圖2電流放大器的PSpice電路圖;(b)相對應的跡線:#1是開回路增益a v,#2和#3是公式(5)右邊的第一和第二分量,#4是整體閉回路增益A。漸近增益模型討論了簡單的II轉換器,我們再用圖5的電路圖對圖1的簡單電路圖作一個概括,稱之為漸近增益模型(asymptotic gain model),該電路給出:
其中:
圖5:考慮誤差放大器的饋通并概括圖1的電路圖。我們應該擔心饋通嗎?將饋通項a ft s I視為一種雜訊形式是有益的,我們將之反映到誤差放大器的輸入,即(a ft s I )/a ε。圖6可以很容易證明這一點。
顯然只要|a ft |<<|a ε |,饋通可能就不會是問題;但是,a ε隨著頻率滾降(rolls off),a ft變得越來越相關,并最終占據主導。
圖6:將饋通建模為一種輸入雜訊形式。我們是否應關心饋通,取決于實際應用。
圖7:使用GBP=1MHz和r o =100Ω的運算放大器來實現積分器。在積分器(integrator)電路中,饋通可能是一個問題。圖7使用了一個1MHz運算放大器,其輸出阻抗r o=100Ω,以接近理想的傳遞函數:
其中f 0是積分器的單位增益頻率:
在f→∞時,傳遞函數應降至零。然而,r o ≠0的存在導致高頻饋通增益a ft (∞)≠0。因為在高頻時C表現為短路,我們有:
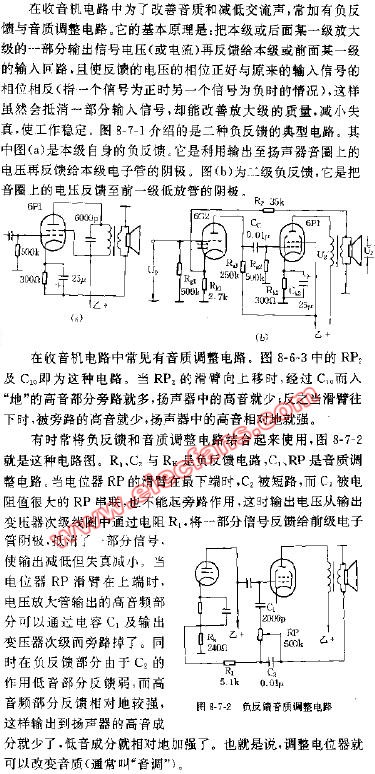
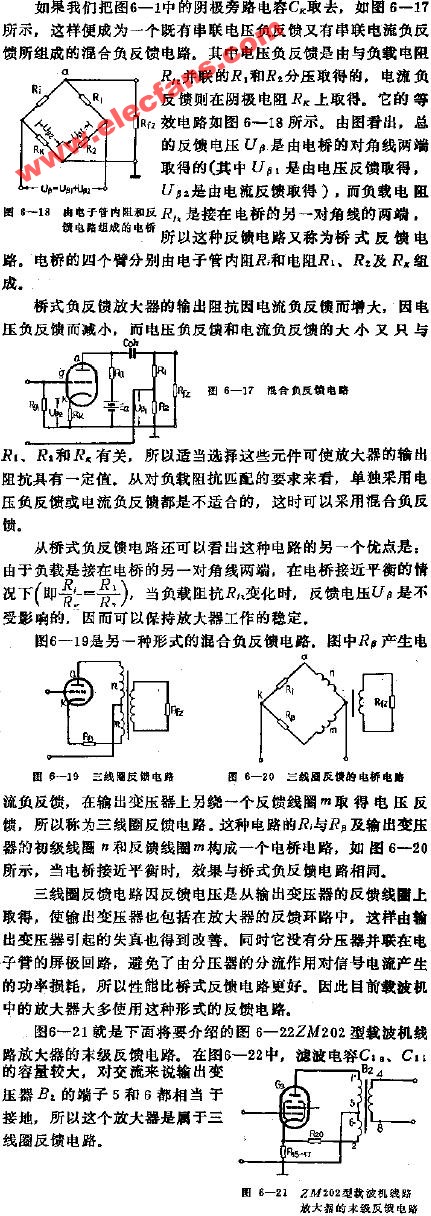
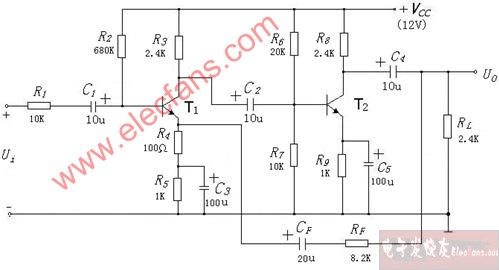
圖8:圖7積分器的頻率特性曲線,跡線#1是開回路增益,跡線#2是理想的積分傳遞函數H ideal,跡線#3是實際傳遞函數H(jf)。圖8顯示實際回應H僅在100H<f<1MHz的范圍內接近H ideal。低于100Hz時,C表現為開路,使運算放大器工作在開回路模式。在1MHz時,差異函數D(jf)出現,導入了新的極點頻率;這使得下降速率加倍,到3MHz左右,饋通出現。如果想讓H更接近H ideal,請使用具有更高GBP的運算放大器。如果饋通在你的應用中是一個問題,可以透過使用具有較低r o的運算放大器或提高R的值來降低a ft(∞)的值(同時降低C的值以保持相同的積分器單位增益頻率)。從圖9a可以看出,串聯輸入運算放大器配置中的饋通往往不那么嚴重,因為輸入電壓V i必須透過運算放大器輸入阻抗z i傳輸,這個阻抗通常很大。需要注意的是,在高頻時z i往往是電容性(capacitive)的,因此會增加饋通量。并聯輸入配置中的饋通更嚴重,因為輸入電流I I直接饋入回饋網路。但要注意,z o可能會在高頻下表現出電感性(inductive behavior),因此其分流減少將允許更多的饋通。對于電流回饋運算放大器(見圖9b),輸入側的情況相反。輸入接腳上緩沖器的輸出阻抗z n通常較小,因此V i透過z n直接饋入回饋網路,而I I則被z n分流到輸入緩沖器。
圖9:(a)電壓回饋;(b)電流回饋運算放大器中的饋通。附錄:電流放大器的直接分析我們看一下如何得到圖2中電流放大器閉回路電流增益A和輸入/輸出電阻R i和R o的運算式。該電路非常簡單,我們可以直接對其進行分析,忽視回饋分析的必要步驟。要得到A,使用圖10a的電路,得到:
其中:
消除v O,整理得到:
圖10:此電路可以得到(a)電流增益A=i O /i I;(b)輸入;(c)圖2中電流放大器的輸出電阻R i和R o。我們也一并找出閉回路終端電阻R i和R o。為了找到輸入源i I所見的電阻R i,利用如圖10b中的測試電流i,得到v:
求解比值R i =v/i,得到:
為了找到負載LD所見的輸出電阻R o,施加一個測試電壓v,如圖10c所示,可以得到i:
其中:
求解比值R o =v/i,得到:
小測驗有四個學生(A、B、C和X)正在討論圖11的VI轉換器,該轉換器使用的運算放大器具有無限大輸入電阻、零輸出電阻,以及很大的開回路增益a v。具體而言,他們試圖找出負載LD所見的輸出電阻R o。
圖11:(a)VI轉換器的理想值i O =(1/R)V i;以及(b)負載所見的電阻R o。A:很明顯,LD往上看到運算放大器的輸出電阻,假設為零;向下只看到R,因為沒有電流流入反相輸入端。因此,R o =0+R=R。X:沒錯!B:錯!透過回饋作用,運算放大器在R和源V i之間建立虛擬短路,這被認為是理想的,因此R o=0+0=0。X:正確!C:我聽說R o應該比較大...X:這就是我一直說的:R o →∞,至少理想情況下是這樣。問題:你覺得上面哪一個學生是對的?
其中A ideal是理想極限a ε →∞時的閉回路增益,a ε是開回路增益,T=a ε /A ideal是回路增益。盡管運算放大器是電壓輸入/電壓輸出(VV)元件,但它可以配置為四種拓撲結構中的任何一種。現在我們來討論II拓撲結構,并由此引出負回饋的其他細節。電流放大器圖2的回饋拓撲結構通常稱為并聯-串聯型,其中具有開回路電壓增益a v的運算放大器被配置為電流放大,其增益可表示為A=i O /i I (除了a v<∞的情況,該運算放大器假定是理想的。另外,為簡單起見,我們假設負載短路,這是電流輸出元件最簡單的負載類型,就像開路是電壓輸出元件最簡單的負載一樣)。
圖2:使用運算放大器作為電流放大器,或II轉換器。要得到A ideal,參考圖3a,我們有:
消除v O,整理得到:
參考圖3b,可以看到沿回路傳輸的訊號v D首先被a v放大,然后通過LD和R 2完整地返回到運算放大器的反相輸入端,因此回路增益僅為T=a v。我們是否可以應用公式(1)得到下面的公式?
讓我們透過PSpice軟體工具來看一些特殊情況,例如R 1 =R 2 =10kΩ和a v =10V/V。然后,公式(3)得出A=2/(1+1/10)=1.818A/A。然而,PSpice卻得出1.909A/A,雖然差別不大,但對于這樣簡單的電路來說絕對是不能接受的。在圖3c中a v →0的情況下甚至出現更大的差異。藉由檢查發現,i O =i I,因此A=i O /i I =1A/A,而公式(3)預測A=2a v /(a v +1)=2x0/(0+1)= 0A/A!
圖3:獲得(a)A ideal;(b)回路增益T; (c)饋通增益a ft的電路。有什么問題?公式(3)的問題在于它試圖使II轉換器符合圖1的電路圖,它假設訊號單向傳輸,即透過放大器正向傳輸,以及透過回饋網路反向傳輸,如圖中的箭頭圖形所示。然而,仔細審視II轉換器就會發現,回饋網路是雙向的,如圖3c所示,在將v N =v O /(1+R 2 /R 1 )回饋回運算放大器的反相輸入時,網路也將i I前饋到負載,繞開了運算放大器。這時,饋通增益為a ft =1A/A。我們該如何考慮這種雙向性?電路很簡單,我們可以直接分析它(參考文后的附錄)。確切的結果是:
這與公式(3)不完全相同。但是,我們可以輕松地將公式(4)重新表達為:
其中最后一項確實考慮了訊號饋通。在我們的范例中(R 1 =R 2 =10kΩ及a v =10V/V),公式(5)得出A=1.818+1/11=1.909A/A,本來就應該這樣。透過PSpice查看各種增益還是很直觀的。圖4a的電路采用了一個直流增益為10V/V、增益頻寬積GBP為10MHz的運算放大器(沒錯,這里特意采用低于標準的運算放大器,以更充分顯示由饋通產生的影響)。從圖4b的跡線(trace)可以看出,只要a v (跡線#1)足夠高,饋通分量(跡線#3)可以忽略不計。然而,a v隨著頻率滾降,饋通變得越來越相關,最終占據主導地位。因此在高頻下,跡線#4與跡線#3匯合,使得A→a ft。
圖4:(a)用于模擬圖2電流放大器的PSpice電路圖;(b)相對應的跡線:#1是開回路增益a v,#2和#3是公式(5)右邊的第一和第二分量,#4是整體閉回路增益A。漸近增益模型討論了簡單的II轉換器,我們再用圖5的電路圖對圖1的簡單電路圖作一個概括,稱之為漸近增益模型(asymptotic gain model),該電路給出:
其中:
圖5:考慮誤差放大器的饋通并概括圖1的電路圖。我們應該擔心饋通嗎?將饋通項a ft s I視為一種雜訊形式是有益的,我們將之反映到誤差放大器的輸入,即(a ft s I )/a ε。圖6可以很容易證明這一點。
顯然只要|a ft |<<|a ε |,饋通可能就不會是問題;但是,a ε隨著頻率滾降(rolls off),a ft變得越來越相關,并最終占據主導。
圖6:將饋通建模為一種輸入雜訊形式。我們是否應關心饋通,取決于實際應用。
圖7:使用GBP=1MHz和r o =100Ω的運算放大器來實現積分器。在積分器(integrator)電路中,饋通可能是一個問題。圖7使用了一個1MHz運算放大器,其輸出阻抗r o=100Ω,以接近理想的傳遞函數:
其中f 0是積分器的單位增益頻率:
在f→∞時,傳遞函數應降至零。然而,r o ≠0的存在導致高頻饋通增益a ft (∞)≠0。因為在高頻時C表現為短路,我們有:
圖8:圖7積分器的頻率特性曲線,跡線#1是開回路增益,跡線#2是理想的積分傳遞函數H ideal,跡線#3是實際傳遞函數H(jf)。圖8顯示實際回應H僅在100H<f<1MHz的范圍內接近H ideal。低于100Hz時,C表現為開路,使運算放大器工作在開回路模式。在1MHz時,差異函數D(jf)出現,導入了新的極點頻率;這使得下降速率加倍,到3MHz左右,饋通出現。如果想讓H更接近H ideal,請使用具有更高GBP的運算放大器。如果饋通在你的應用中是一個問題,可以透過使用具有較低r o的運算放大器或提高R的值來降低a ft(∞)的值(同時降低C的值以保持相同的積分器單位增益頻率)。從圖9a可以看出,串聯輸入運算放大器配置中的饋通往往不那么嚴重,因為輸入電壓V i必須透過運算放大器輸入阻抗z i傳輸,這個阻抗通常很大。需要注意的是,在高頻時z i往往是電容性(capacitive)的,因此會增加饋通量。并聯輸入配置中的饋通更嚴重,因為輸入電流I I直接饋入回饋網路。但要注意,z o可能會在高頻下表現出電感性(inductive behavior),因此其分流減少將允許更多的饋通。對于電流回饋運算放大器(見圖9b),輸入側的情況相反。輸入接腳上緩沖器的輸出阻抗z n通常較小,因此V i透過z n直接饋入回饋網路,而I I則被z n分流到輸入緩沖器。
圖9:(a)電壓回饋;(b)電流回饋運算放大器中的饋通。附錄:電流放大器的直接分析我們看一下如何得到圖2中電流放大器閉回路電流增益A和輸入/輸出電阻R i和R o的運算式。該電路非常簡單,我們可以直接對其進行分析,忽視回饋分析的必要步驟。要得到A,使用圖10a的電路,得到:
其中:
消除v O,整理得到:
圖10:此電路可以得到(a)電流增益A=i O /i I;(b)輸入;(c)圖2中電流放大器的輸出電阻R i和R o。我們也一并找出閉回路終端電阻R i和R o。為了找到輸入源i I所見的電阻R i,利用如圖10b中的測試電流i,得到v:
求解比值R i =v/i,得到:
為了找到負載LD所見的輸出電阻R o,施加一個測試電壓v,如圖10c所示,可以得到i:
其中:
求解比值R o =v/i,得到:
小測驗有四個學生(A、B、C和X)正在討論圖11的VI轉換器,該轉換器使用的運算放大器具有無限大輸入電阻、零輸出電阻,以及很大的開回路增益a v。具體而言,他們試圖找出負載LD所見的輸出電阻R o。
圖11:(a)VI轉換器的理想值i O =(1/R)V i;以及(b)負載所見的電阻R o。A:很明顯,LD往上看到運算放大器的輸出電阻,假設為零;向下只看到R,因為沒有電流流入反相輸入端。因此,R o =0+R=R。X:沒錯!B:錯!透過回饋作用,運算放大器在R和源V i之間建立虛擬短路,這被認為是理想的,因此R o=0+0=0。X:正確!C:我聽說R o應該比較大...X:這就是我一直說的:R o →∞,至少理想情況下是這樣。問題:你覺得上面哪一個學生是對的?
 電子發燒友App
電子發燒友App










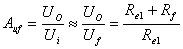



















評論