本文主要介紹小波分解與重構法、非線性小波變換閾值法、平移不變量小波法以及小波變換模極大值法這4種常用的小波去噪方法。將它們分別用于仿真算例的去噪處理，并對這幾種方法的應用場合、去噪性能、計算速度和影響因素等方面進行比較。

選擇了Matlab軟件中的仿真信號Blocks作為原始信號，信號長度（即采樣點數）N=2048，如圖1a所示。由于該信號中含有若干不連續點和奇異點，因此用以下幾種方法對圖1b中疊加了高斯白噪聲的Blocks信號（信噪比為7）進行去噪處理，能夠很清楚地比較出這幾種方法的去噪性能。

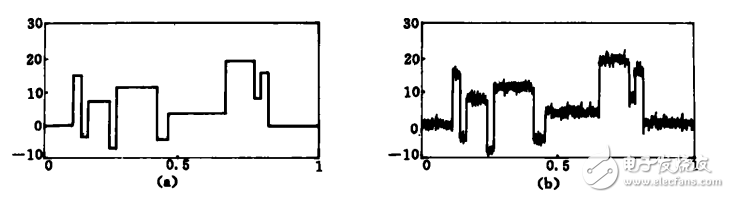
圖1 ?原始信號和含噪信號的時域波形

一、小波去噪方法

1、小波分解與重構法去噪

小波分解與重構的快速算法，即Mallet算法。據這一算法，若fk為信號f（t）的離散采樣數據，fk=c0，k，則信號f（t）的正交小波變換分解公式為：

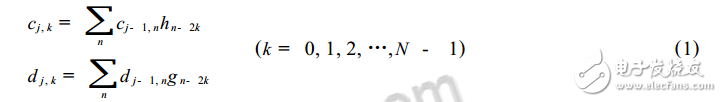
其中，cj，k為尺度系數;dj，k為小波系數;h、g為一對正交鏡像濾波器組（QMF）;j為分解層數;N為離散采樣點數。

小波重構過程是分解過程的逆運算，相應的重構公式為：

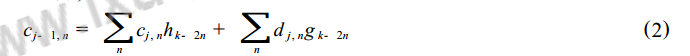
小波的多分辨分析特性能將信號在不同尺度下進行多分辨率的分解，并將交織在一起的各種不同頻率組成的混合信號分解成不同頻段的子信號，因而對信號具有按頻帶處理的能力。應用小波分解與重構的方法去噪具體步驟是：根據需要，將含有噪聲信號在某一尺度下分解到不同的頻帶內，然后再將噪聲所處的頻帶置零（或直接提取有用信號所在的頻帶），進行小波重構，從而達到去噪的目的。

圖2是用小波分解與重構法進行去噪的結果。采用的小波是近似對稱的Symmlet8小波，小波分解層數是4，其中圖2a是將圖1b中的含噪信號進行4層小波分解的結果。從中可以看出，信號的能量主要集中于低頻的少數小波系數上，而噪聲的能量則分散于整個小波變換域。圖2b是提取圖2a中的前256個小波系數進行重構，也就是提取尺度4上的低頻系數和高頻系數進行重構的結果。

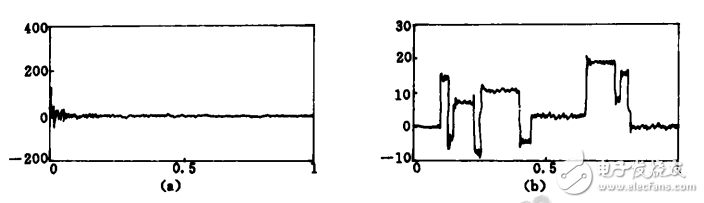
圖2 ?小波分解與重構法去噪

2、非線性小波變換閾值法去噪

非線性小波變換閾值法也稱為“小波收縮”（waveletshrinkage），其去噪方法如下：

假設一個疊加了高斯白噪聲的有限長信號可以表示為

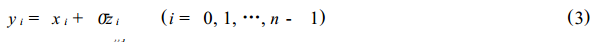
其中，zi是一個標準的高斯白噪聲，即z～N（0，1），R是噪聲級。若要從被噪聲污染的信號yi中恢復出原始信號xi，則Donoho的去噪方法分為以下3個步驟：

（1）計算含噪聲信號的正交小波變換。選擇合適的小波和小波分解層數j，將含噪信號運用（1）式進行小波分解至j層，得到相應的小波分解系數。

（2）對分解得到的小波系數進行閾值處理，其閾值的處理方法有2種：

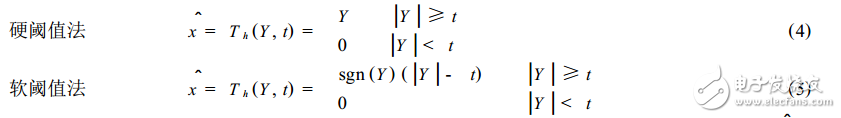
（3）進行小波逆變換。將經閾值處理過的小波系數用（2）式重構，得到恢復的原始信號估計值xd。

小波變換具有一種“集中”的能力，它能將信號的能量集中到少數小波系數上;而白噪聲在任何正交

基上的變換仍然是白噪聲，并且有著相同的幅度。相對來說，信號的小波系數值必然大于那些能量分散且幅值較小的噪聲的小波系數值。選擇一個合適的閾值，對小波系數進行閾值處理，就可以達到去除噪聲而保留有用信號的目的。該方法能得到原始信號的近似最優估計，并且具有非常廣泛的適應性。

圖3和圖4分別是采用Donoho的非線性小波變換閾值法以及平移不變量小波法去噪得到的結果。這2種方法均選用Haar小波，小波分解層數是5。二者均采用軟閾值，閾值大小t=2log（N），其中N為信號長度。

圖3 ?軟閾值法去噪

圖4 ?平移不變量小波法去噪

3、平移不變量小波去噪

平移不變量小波去噪法是在閾值法基礎上的改進。雖然用閾值法能取得很好的去噪效果，但在有些情況下，如在信號的不連續鄰域，閾值法去噪會表現出視覺上的非自然信號，如偽吉布斯現象，即不連續點附近的信號會在一個特定的目標水平上下跳變。利用平移不變量法去噪，則可有效地抑制這種現象。其方法是：對含噪聲信號進行n次循環平移，對平移后的信號進行的閾值法去噪處理，然后再對去噪的結果進行平均，這就是所謂的“平移-去噪-平均”的平移不變量小波去噪法。

對于一個信號xt（0≤t≤n），Hn={h∶0≤h《n}，用Sh表示對信號xt進行h的時域平移，h是正整數，T表示對信號用Donoho的閾值法進行去噪處理，Ave表示“平均”，S-h=（Sh）-1，則n次循環平移的平移不變量小波去噪方法可以表示為：

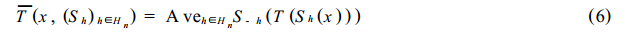
該方法在去除偽吉布斯現象，表現出更好的視覺效果的同時，還能夠得到比閾值法去噪更小的均方根誤差（RMSE），并且提高了信噪比（SRN）。

4、小波變換模極大值法去噪

信號的奇異點就是指信號中的突變點，Lip指數是表征信號局部奇異點特征的一種量度，它的定義如下：設有正整數n，n≤A≤n+1，如果存在正整數A》0及n次多項式pn（x），使得：

由（8）式可知，對于一般信號，由于A≥0，小波變換的模極大值將隨著j的增大而增大;而對于白噪聲，由于A《0，其模極大值隨著j的增大而減小。因此，觀察不同尺度間小波變換模極大值變化的規律，去除幅度隨尺度的增加而減小的點（對應噪聲的極值點），保留幅度隨尺度增加而增大的點（對應于有用信號的極值點），然后再由保留的模極大值點用交替投影法進行重建，即可以達到去噪的目的。

圖5是用小波變換模極大值法去噪的結果。所采用的是雙正交樣條小波，小波分解層數是2。

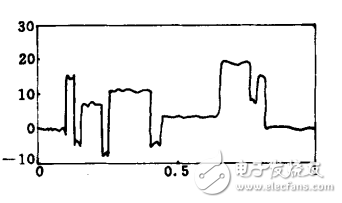
圖5 ?小波變換模極大值法去噪

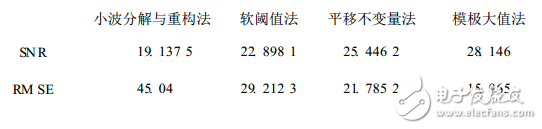
表1中列出了用這4種方法去噪，信號的信噪比（SNR）和均方根誤差（RMSE）的比較。從信噪比和均方根誤差的角度看，模極大值法的去噪性能最好，小波分解與重構法最差，閾值法和平移不變量法居中。

表1 ?幾種方法去噪后SNR和RMSE的比較

二、小波去噪方法的比較

1、小波分解與重構法去噪

本質上相當于一個具有多個通道的帶通濾波器，主要適用于有用信號和噪聲的頻帶相互分離時的確定性噪聲的情況。在這種情況下，該方法能基本去除噪聲，去噪效果很好。但對于有用信號和噪聲的頻帶相互重疊的情況（如信號混有白噪聲），效果就不甚理想。這種方法的優點是算法簡單明了，計算速度快。若N為信號的長度，則它的計算速度是O（N）。其缺點是適用范圍不是很廣泛。它對于特定情況下已知道噪聲的頻率范圍且信號和噪聲的頻帶相互分離時非常有效。對實際應用中廣泛存在的白噪聲，其去噪效果則較差。

2、非線性小波變換閾值法去噪

主要適用于信號中混有白噪聲的情況。用閾值法去噪的優點是噪聲幾乎完全得到抑制，且反映原始信號的特征尖峰點得到很好的保留。用軟閾值的方法去噪能夠使估計信號實現最大均方誤差最小化，即去噪后的估計信號是原始信號的近似最優估計;且估計信號至少和原始信號同樣光滑而不會產生附加振蕩。該方法還具有廣泛的適應性，因而是眾多小波去噪方法中應用最為廣泛的一種。閾值法的計算速度很快，為O（N），其中N為信號長度。其缺點是在有些情況下，如在信號的不連續點處，去噪后會出現偽吉布斯現象。且用該方法去噪時，閾值的選擇對去噪效果有著很重要的影響。閾值的選擇方法有多種，實際應用時應根據具體的情況來選擇合適的閾值。

3、平移不變量小波法去噪

主要適用于信號中混有白噪聲且含有若干不連續點的情況，是在閾值法基礎上的改進。其優點可以有效地去除閾值法去噪中，在信號的不連續點處所產生的偽吉布斯現象，表現出比閾值法更好的視覺效果。從L2范數誤差的觀點看，經該方法去噪能夠得到比閾值法更小的均方根誤差，信噪比也得到一定地提高;缺點是計算速度沒有閾值法快。當信號長度是N時，計算速度是O（NlogN）。

4、模極大值法去噪

主要適用于信號中混有白噪聲，且信號中含有較多奇異點的情況。該方法在去噪的同時，有效地保留信號的奇異點信息，去噪后的信號沒有多余振蕩，是原始信號的一個非常好的估計，具有較好的圖面質量。用模極大值進行重構時采用的是交替投影法，為保證重構信號的精度，提高信噪比，通常要進行幾十次的迭代，每迭代一次的速度是O（NlogN）。因此，計算速度非常慢，通常要比前幾種方法慢數十倍。