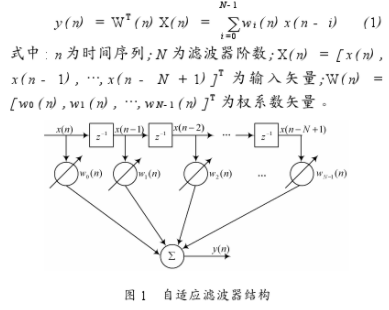
MATLAB語言簡介

　　MATLAB是美國MathWorks公司開發的大型數學計算應用軟件系統，它提供了強大的矩陣處理和繪圖功能，簡單易用，可信度高，靈活性好，因而在世界范圍內被科學工作者、工程師以及大學生和研究生廣泛使用，目前已經成為國際市場上科學研究和工程應用方面的主導軟件。掌握MATLAB并借助它解決理論與應用問題已經成為每一個從事科學研究和工程技術人員應該具備的技能。

　　MATLAB是Matrix Laboratory（矩陣實驗室）的縮寫，是當前最流行、功能強大的科技應用軟件和編程語言之一。MATLAB語言有以下特點：

　　1、功能強大：數值計算和符號計算，計算和編程可視化，數字和文字的統一處理，離線和在線計算；

　　2、界面友好，語言簡明：以復數矩陣為計算單元，指令表達與數學表達式相近，是一種演算式語言；

　　3、開放性強：具有70余個功能強大的工具箱，覆蓋面極廣，可以完成數字圖像處理、系統仿真、系統辨識、模糊控制、神經網絡建模、信號處理、魯棒控制、非線性控制、優化理論、統計分析等。

　　MATLAB成為應用學科計算機輔助分析、設計、仿真、教學必不可少的基礎軟件。工具箱函數為各個領域的研究和工程應用提供了有力的手段。

　　MATLAB系統的基本函數庫具有初等函數、初等矩陣和矩陣變換、包括性代數方程組和矩陣特征值問題等數值線性代數、多項式運算和求根、數據析和傅立葉變換以及某些特殊的矩陣函數和數學函數等眾多內容。

　　MATLAB還包括一系列被稱作工具箱（TOOLBOX）的專業求解工具。工具箱實際上是MATLAB針對不同學科、不同專業所開發的專用函數庫，用來求解各個領域的數值計算問題，包括數據采集工具箱、信號處理工具箱、圖像處理工具箱、小波分析工具箱、控制工具箱等。隨著MATLAB的不斷升級，所含工具箱的功能越來越豐富，規模越來越龐大，因此，應用也越來越廣泛，成為各種專業科研人員和工程技術人員的得力工具。

　　一個圖形界面的完成，最終是通過圖形界面的各種控件對象的操作來完成，而這些操作必定是通過Matlab 中函數代碼的執行來完成的。函數代碼的編制可以通過編寫回調函數完成，而編寫時當所要求執行的指令比較簡單時，可以把該控件的代碼直接寫在“CallBack“屬性中；當所要求執行的指令比較長時可以把函數代碼放在一個自定義的M 文件中，在“CallBack”中直接將其文件名寫上，也可以在主控文件中直接編寫，當操作該控件時系統會自動執行“CallBack”中所要求執行的內容。

　　在本設計中，采用的是在主控文件中直接編寫的方法，在GUI 界面單擊當前需要編寫程序的控件，然后右擊將出現一個右鍵菜單，然后選擇Callback 選項，即可直接進入主控M 文件，并且系統會自動生成語句。

　　目前的MATLAB已經成為國際上最為流行的軟件之一，它除了傳統的交互式編程之外，還提供了豐富可靠的矩陣運算、圖形繪制、數據處理、圖形處理，方便的windows編程等便利工具，出現了各種以MATLAB為基礎的實用工具箱，廣泛地應用于自動控制、圖像信號處理、生物醫學工程、語言處理、雷達工程、信號分析、振動理論、時序分析于建模、優化設計等領域。

　　算法實現設計

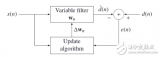
　　本課題的主要內容是在MATLAB上實現自適應濾波器的設計。課題的具體內容

　　為利用GUI界面設計出濾波器的選擇界面、參數的輸入界面、結果分析圖等。其中濾波器的設計將會用兩種算法實現既LMS算法和RLS算法，算法實現的基本設計框圖如圖4所示。

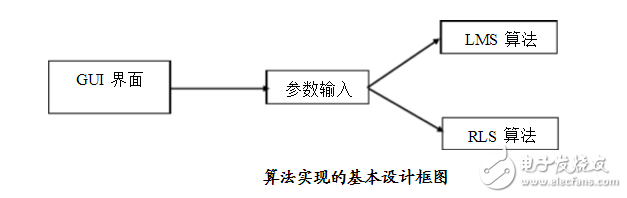
　　GUI界面的設計

　　由于本論文要實現兩種不同的算法，通過GUI界面設計能給人一個比較好直觀的效果。同時兩種算法在參數取值方面會有不同之處，因此在軟件設計中，我通過文本編輯框控件來接收用戶輸入的濾波器設計指標值，這讓我們能更方便的通過調整不同的參數值觀測實驗結果，從而來保證濾波器的最佳狀態。此外，Matlab 通過創建應用程序M 文件為GUI控制程序提供一個框架。所有代碼都包含在應用程序M 文件中，即完成了圖形界面的設計后，應用程序設計的主要工作是控件回調函數的設計。自適應濾波算法的主界面如圖5。

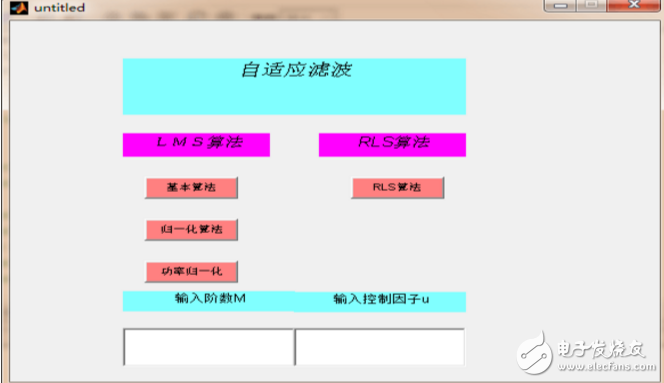
　　LMS算法的實現

　　LMS算法實現流程圖如圖6。

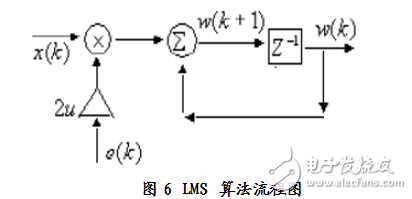
　　在圖中，w（k）為濾波器濾波系數矢量估值，w（k+1）=w（k）-u，u是一個控制因子，用它來控制收斂速度與穩定性，u太大不穩定，u太小收斂速度很慢。通常0《u《1/max，max是R中的最大的特征值。（k）是誤差梯度，直接計算（k）=J（w）/w很復雜，一般直接用誤差的平方作為均方誤差E|e（k）2估計值（k）。因為E{（k）}=k表明（k）是無偏估計。

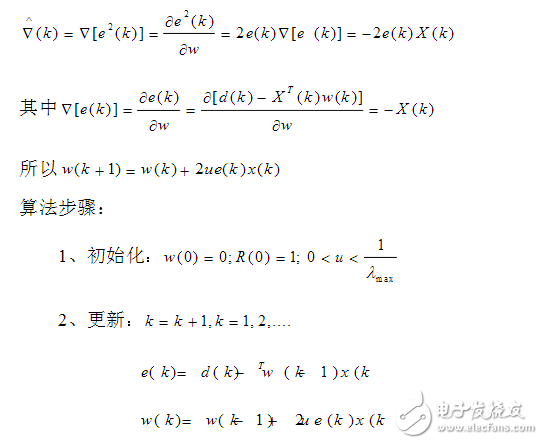
　　直到計算到達到（e）k預期小的值為止，或（w）k達到穩定為止。

　　根據u的取值不同LMS算法可分為以下三種類型：

　　方案1——基本的LMS算法的實現

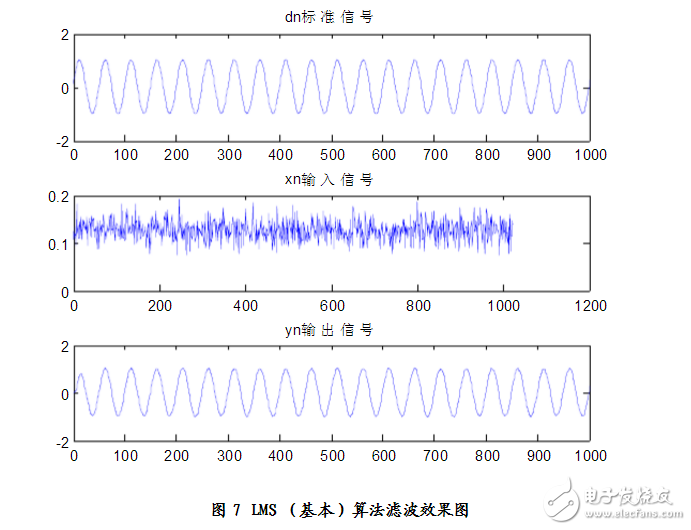
　　原信號與噪聲信號相互獨立，我們采用高斯白噪聲作為噪聲信號代替，并且定義噪聲信號的功率為0.02，E（（r（n））^2）=0.02，則v（n）=0.02*randn（1，1024）。基本的LMS算法要求控制因子u（k）為常數，所以在設計時我們得根據仿真結果來選擇合適的u（k），以達到濾波器的最優濾波性能。為了完成輸出信號與標準信號的對比，還必須定義一個標準信號，我們定義標準信號為正弦信號，這樣方便我們更好的觀測仿真數據。此外，定義w（n）為濾波器濾波系數矢量估值。最后，到了濾波器設計的關鍵階段—算法的編程，我采用了for語句來實現算法的循環，直到計算到e（n）預期小的值為止或w（n）達到穩定為止。

　　算法編程如下：

　　for n=2:M

　　xn=sin（4*pi*n/100）+vn;

　　yn（n）=w1（n）*xn（n）+w2（n）*xn（n-1）;

　　e（n）=xn（n）-yn（n）;

　　w1（n+1）=w1（n）+2*u*e（n）*xn（n）;

　　w2（n+1）=w2（n）+2*u*e（n）*xn（n-1）;

　　end

　　仿真結果：

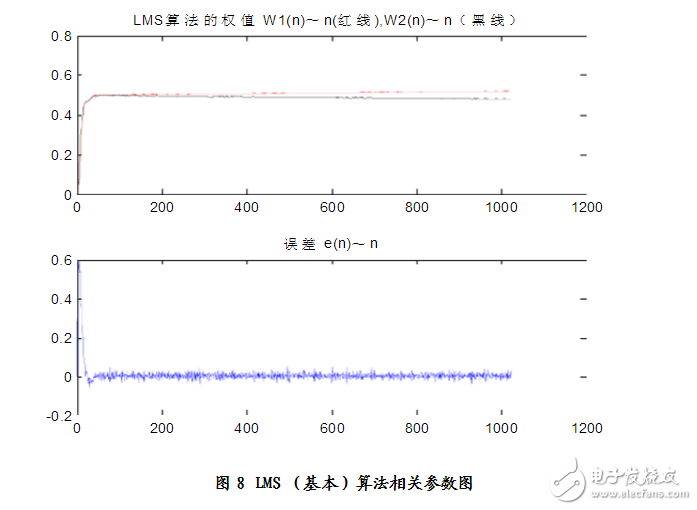
　　見圖7、圖8 分析可得：n=20

　　Elapsed time is 0.094000 seconds.

　　方案2——歸一化LMS算法的實現

　　歸一化算法與基本的LMS算法在思路上沒有多大差別，就只是在對u（k）的選取方面有一定的差別，歸一化中定義a（0，2），p》0因此，在for語句中需要對u（k）的取值加額外的要求。為了方便起見，我們暫且定義a=o，p=o

　　歸一化LMS算法編程為：

　　for n=2:M

　　xn=sin（4*pi*n/100）+vn;

　　yn（n）=w1（n）*xn（n）+w2（n）*xn（n-1）;

　　e（n）=xn（n）-yn（n）; u（n）=1/（xn*xn‘）;

　　w1（n+1）=w1（n）+2*u（n）*e（n）*xn（n）;

　　w2（n+1）=w2（n）+2*u（n）*e（n）*xn（n-1）;

　　end

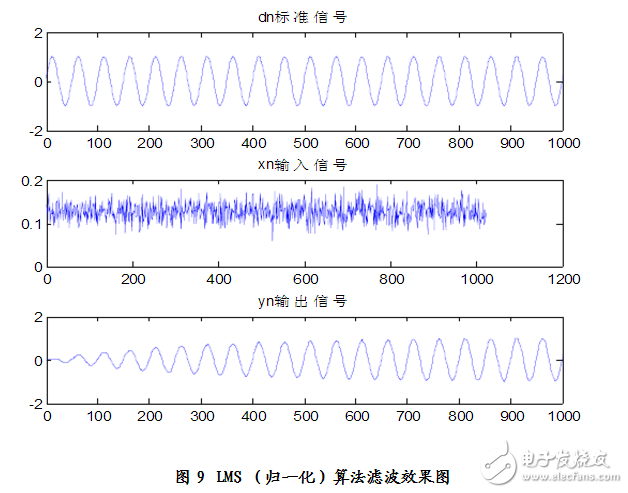
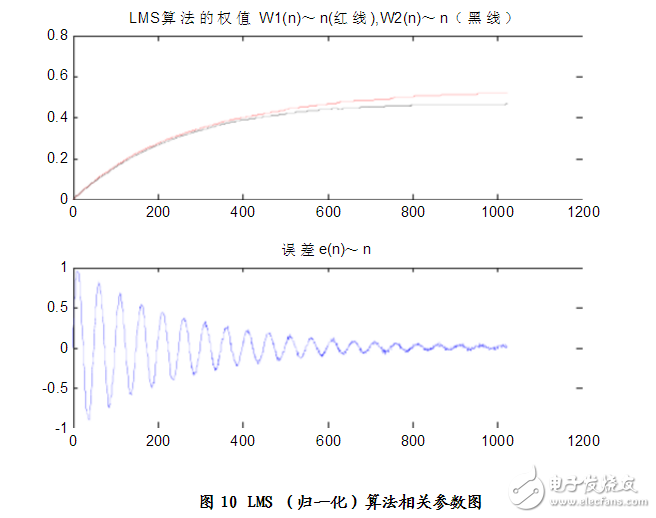
　　仿真結果：見圖9、圖10

　　分析可得：n=600

　　Elapsed time is 0.094000 seconds.

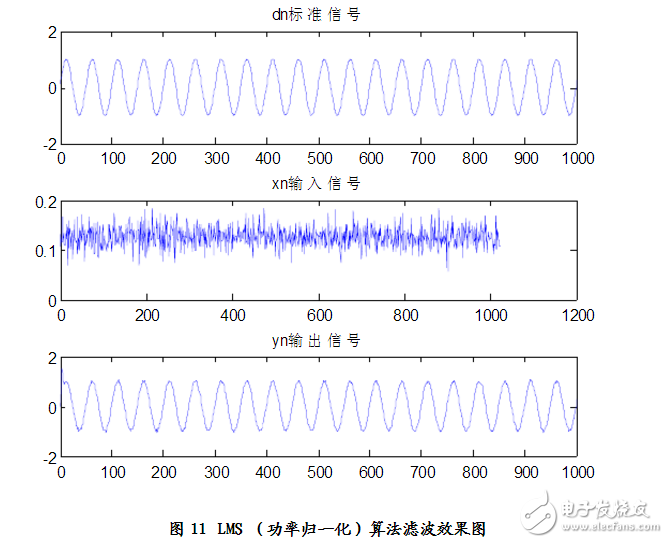
　　方案3——功率歸一化LMS算法的實現

　　功率歸一化，與歸一化算法一樣，也只是在對u（k）的取值方面有一定的差別。功率歸一化中定義u（k）=a/g2x（k），其中g2x表示x（k）的方差。由a/g2x（k）=dg2x（k-1）+e2（k）可知，d《（0，1），0《a《2/m，其中M為濾波器的階數。同時也為了方便起見，我們暫且定義a=1/M，d=0.5。

　　功率歸一化LMS算法編程為：

　　for n=2:M

　　xn=sin（4*pi*n/100）+vn;

　　yn（n）=w1（n）*xn（n）+w2（n）*xn（n-1）;

　　e（n）=xn（n）-yn（n）;

　　gx2（n）=d*gx2（n-1）+e（n）*e（n）; u（n）=a/（gx2（n））;

　　w1（n+1）=w1（n）+2*u（n）*e（n）*xn（n）;

　　w2（n+1）=w2（n）+2*u（n）*e（n）*xn（n-1）;

　　end

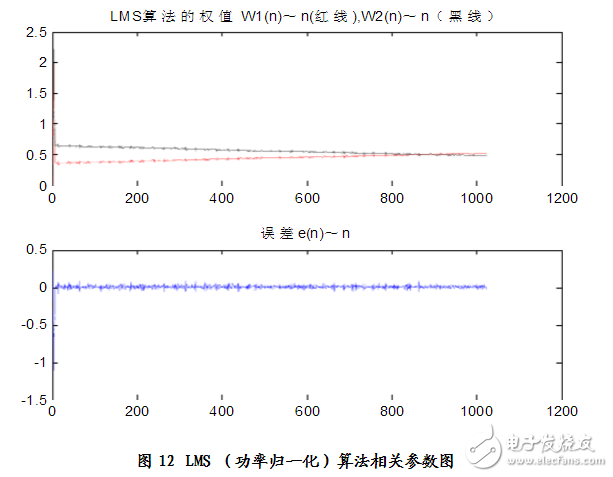
　　仿真結果：見圖11、圖12

　　分析得：n=8

　　Elapsed time is 0.078000 seconds.

　　LMS（least mean square）自適應濾波算法matlab實現

　　以下是matlab幫助文檔中lms示例程序，應用在一個系統辨識的例子上。整個濾波的過程就兩行，用紅色標識。

　　x = randn（1，500）; % Input to the filter

　　b = fir1（31，0.5）; % FIR system to be identified

　　n = 0.1*randn（1，500）; % Observation noise signal

　　d = filter（b，1，x）+n; % Desired signal

　　mu = 0.008; % LMS step size.

　　ha = adaptfilt.lms（32，mu）;

　　［y，e］ = filter（ha，x，d）;

　　subplot（2，1，1）; plot（1:500，［d;y;e］）;

　　title（‘System Identification of an FIR Filter’）;

　　legend（‘Desired’，‘Output’，‘Error’）;

　　xlabel（‘Time Index’）; ylabel（‘Signal Value’）;

　　subplot（2，1，2）; stem（［b.‘，ha.coefficients.’］）;

　　legend（‘Actual’，‘Estimated’）;

　　xlabel（‘Coefficient #’）; ylabel（‘Coefficient Value’）;

　　grid on;

　　這實在看不出什么名堂，就學習目的而言，遠不如自己寫一個出來。整個濾波的過程用紅色標識。

　　%% System Identification （SID）

　　% This demonstration illustrates the application of LMS adaptive filters to

　　% system identification （SID）。

　　%

　　% Author（s）： X. Gumdy

　　% Copyright 2008 The Funtech， Inc.

　　%% 信號產生

　　clear all;

　　N = 1000 ;

　　x = 10 * randn（N，1）; % 輸入信號

　　b = fir1（31，0.5）; % 待辨識系d

　　n = randn（N，1）;

　　d = filter（b，1，x）+n; % 待辨識系統的加噪聲輸出

　　%% LMS 算法手工實現

　　sysorder = 32;

　　maxmu = 1 / （x‘*x / N * sysorder）;% 通過估計tr（R）來計算mu的最大值

　　mu = maxmu / 10;

　　w = zeros （ sysorder ， 1 ） ;

　　for n = sysorder ： N

　　u = x（n-sysorder+1:n） ;

　　y（n）= w’ * u;

　　e（n） = d（n） - y（n） ;

　　w = w + mu * u * e（n） ;

　　end

　　y = y‘;

　　e = e’;

　　%% 畫圖

　　figure（1）;

　　subplot（2，1，1）; plot（（1:N）‘，［d，y，e］）;

　　title（’System Identification of an FIR Filter‘）;

　　legend（’Desired‘，’Output‘，’Error‘）;

　　xlabel（’Time Index‘）; ylabel（’Signal Value‘）;

　　subplot（2，1，2）; stem（［b’， w］）;

　　legend（‘Actual’，‘Estimated’）;

　　xlabel（‘Coefficient #’）; ylabel（‘Coefficient Value’）;

　　grid on;