一、最小均方算法(LMS)概述
1959年,Widrow和Hoff在對(duì)自適應(yīng)線性元素的方案一模式識(shí)別進(jìn)行研究時(shí),提出了最小均方算法(簡(jiǎn)稱LMS算法)。LMS算法是基于維納濾波,然后借助于最速下降算法發(fā)展起來(lái)的。通過(guò)維納濾波所求解的維納解,必須在已知輸入信號(hào)與期望信號(hào)的先驗(yàn)統(tǒng)計(jì)信息,以及再對(duì)輸入信號(hào)的自相關(guān)矩陣進(jìn)行求逆運(yùn)算的情況下才能得以確定。因此,這個(gè)維納解僅僅是理論上的一種最優(yōu)解。所以,又借助于最速下降算法,以遞歸的方式來(lái)逼近這個(gè)維納解,從而避免了矩陣求逆運(yùn)算,但仍然需要信號(hào)的先驗(yàn)信息,故而再使用瞬時(shí)誤差的平方來(lái)代替均方誤差,從而最終得出了LMS算法。
因LMS算法具有計(jì)算復(fù)雜程度低、在信號(hào)為平穩(wěn)信號(hào)的環(huán)境中的收斂性好、其期望值無(wú)偏地收斂到維納解和利用有限精度實(shí)現(xiàn)算法時(shí)的穩(wěn)定性等特性,使LMS算法成為自適應(yīng)算法中穩(wěn)定性最好、應(yīng)用最廣泛的算法。
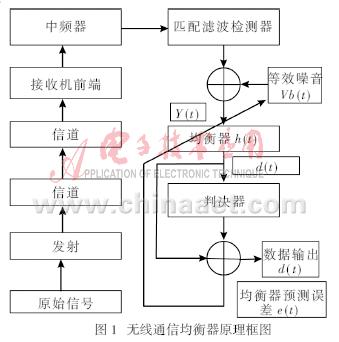
下圖是實(shí)現(xiàn)算法的一個(gè)矢量信號(hào)流程圖:
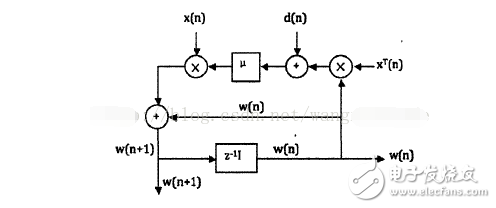
圖1 LMS算法矢量信號(hào)流程圖
由圖1我們可以知道,LMS算法主要包含兩個(gè)過(guò)程:濾波處理和自適應(yīng)調(diào)整。
一般情況下,LMS算法的具體流程為:
(1)確定參數(shù):全局步長(zhǎng)參數(shù)β以及濾波器的抽頭數(shù)(也可以稱為濾波器階數(shù))
(2)對(duì)濾波器初始值的初始化
(3)算法運(yùn)算過(guò)程:
濾波輸出:y(n)=wT(n)x(n)
誤差信號(hào):e(n)=d(n)-y(n)
權(quán)系數(shù)更新:w(n+1)=w(n)+βe(n)x(n)
二、性能分析
在很大程度上,選取怎樣的自適應(yīng)算法決定著自適應(yīng)濾波器是否具有好的性能。因此,對(duì)應(yīng)用最為廣泛的算法算法進(jìn)行性能分析則顯得尤為重要。平穩(wěn)環(huán)境下算法的主要性能指標(biāo)有收斂性、收斂速度、穩(wěn)態(tài)誤差和計(jì)算復(fù)雜度等。
1、收斂性
收斂性就是指,當(dāng)?shù)螖?shù)趨向于無(wú)窮時(shí),濾波器權(quán)矢量將達(dá)到最優(yōu)值或處于其附近很小的鄰域內(nèi),或者可以說(shuō)在滿足一定的收斂條件下,濾波器權(quán)矢量最終趨近于最優(yōu)值。
2、收斂速度
收斂速度是指濾波器權(quán)矢量從最初的初始值向其最優(yōu)解收斂的快慢程度,它是判斷LMS算法性能好壞的一個(gè)重要指標(biāo)。
3、穩(wěn)態(tài)誤差
穩(wěn)態(tài)誤差,是指當(dāng)算法進(jìn)入穩(wěn)態(tài)后濾波器系數(shù)與最優(yōu)解之間距離的遠(yuǎn)近情況。它也是一個(gè)衡量LMS算法性能好壞的重要指標(biāo)。
4、計(jì)算復(fù)雜度
計(jì)算復(fù)雜度,是指在更新一次濾波器權(quán)系數(shù)時(shí)所需的計(jì)算量。LMS算法的計(jì)算復(fù)雜度還是很低的,這也是它的一大特點(diǎn)。
三、LMS算法分類
1、量化誤差LMS算法
在回聲消除和信道均衡等需要自適應(yīng)濾波器高速工作的應(yīng)用中,降低計(jì)算復(fù)雜度是很重要的。LMS算法的計(jì)算復(fù)雜度主要來(lái)自在進(jìn)行數(shù)據(jù)更新時(shí)的乘法運(yùn)算以及對(duì)自適應(yīng)濾波器輸出的計(jì)算,量化誤差算法就是一種降低計(jì)算復(fù)雜度的方法。其基本思想是對(duì)誤差信號(hào)進(jìn)行量化。常見(jiàn)的有符號(hào)誤差LMS算法和符號(hào)數(shù)據(jù)LMS算法。
2、解相關(guān)LMS算法
在LMS算法中,有一個(gè)獨(dú)立性假設(shè)橫向?yàn)V波器的輸入u(1),u(2),…, u(n-1)是彼此統(tǒng)計(jì)獨(dú)立的向量序列。當(dāng)它們之間不滿足統(tǒng)計(jì)獨(dú)立的條件時(shí),基本LMS算法的性能將下降,尤其是收斂速度會(huì)比較慢。為解決此問(wèn)題,提出了解相關(guān)算法。研究表明,解相關(guān)能夠有效加快LMS算法的收斂速度。解相關(guān)LMS算法又分為時(shí)域解相關(guān)LMS算法和變換域解相關(guān)LMS算法。
3、并行延時(shí)LMS算法
在自適應(yīng)算法的實(shí)現(xiàn)結(jié)構(gòu)中,有一類面向VLSI的脈動(dòng)結(jié)構(gòu),由于其具有的高度并行性和流水線特性而備受關(guān)注。將算法直接映射到脈動(dòng)結(jié)構(gòu)時(shí),在權(quán)值更新和誤差計(jì)算中存在著嚴(yán)重的計(jì)算瓶頸。該算法解決了算法到結(jié)構(gòu)的計(jì)算瓶頸問(wèn)題,但當(dāng)濾波器階數(shù)較長(zhǎng)時(shí),算法的收斂性能會(huì)變差,這是由于其本身所具有的延時(shí)影響了它的收斂性能。可以說(shuō),延時(shí)算法是以犧牲算法的收斂性能為代價(jià)的。
4、自適應(yīng)格型LMS算法
LMS濾波器屬于橫向自適應(yīng)濾波器且假定階數(shù)固定,然而在實(shí)際應(yīng)用中,橫向?yàn)V波器的最優(yōu)階數(shù)往往是未知的,需要通過(guò)比較不同階數(shù)的濾波器來(lái)確定最優(yōu)的階數(shù)。當(dāng)改變橫向?yàn)V波器的階數(shù)時(shí),LMS算法必須重新運(yùn)行,這顯然不方便而且費(fèi)時(shí)。格型濾波器解決了這一問(wèn)題。
格型濾波器具有共軛對(duì)稱的結(jié)構(gòu),前向反射系數(shù)是后向反射系數(shù)的共軛,其設(shè)計(jì)準(zhǔn)則和LMS算法一樣是使均方誤差最小。
5、Newton-LMS算法
Newton-LMS算法是對(duì)環(huán)境信號(hào)二階統(tǒng)計(jì)量進(jìn)行估計(jì)的算法。其目的是為了解決輸入信號(hào)相關(guān)性很高時(shí)算法收斂速度慢的問(wèn)題。一般情況下,牛頓算法能夠快速收斂,但對(duì)R-1的估計(jì)所需計(jì)算量很大,而且存在數(shù)值不穩(wěn)定的問(wèn)題。
四、LMS算法基本原理
根據(jù)小均方誤差準(zhǔn)則以及均方誤差曲面,自然的我們會(huì)想到沿每一時(shí)刻均方誤差 的陡下降在權(quán)向量面上的投影方向更新,也就是通過(guò)目標(biāo)函數(shù)k反梯度向量來(lái)反 復(fù)迭代更新。由于均方誤差性能曲面只有一個(gè)唯一的極小值,只要收斂步長(zhǎng)選擇恰當(dāng), 不管初始權(quán)向量在哪,后都可以收斂到誤差曲面的小點(diǎn),或者是在它的一個(gè)鄰域內(nèi)。 這種沿目標(biāo)函數(shù)梯度反方向來(lái)解決小化問(wèn)題的方法,我們一般稱為速下降法,表達(dá)式如下:
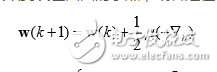
基于隨機(jī)梯度算法的小均方 自適應(yīng)濾波算法的完整表達(dá)式如下:
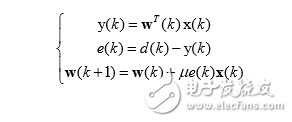
LMS 自適應(yīng)算法是一種特殊的梯度估計(jì),不必重復(fù)使用數(shù)據(jù),也不必對(duì)相關(guān)矩陣 和互相關(guān)矩陣 進(jìn)行運(yùn)算,只需要在每次迭代時(shí)利用輸入向量和期望響應(yīng),結(jié)構(gòu)簡(jiǎn)單, 易于實(shí)現(xiàn)。雖然 LMS 收斂速度較慢,但在解決許多實(shí)際中的信號(hào)處理問(wèn)題,LMS 算法 是仍然是好的選擇。
3 LMS算法性能分析
隨機(jī)梯度 LMS 算法的性能前人有過(guò)大量研究,按照前一章所提到的自適應(yīng)濾波性能 指標(biāo),假設(shè)輸入信號(hào)和期望信號(hào)具有聯(lián)合平穩(wěn)性,詳細(xì)討論基于橫向 FIR 結(jié)構(gòu)的濾波器 的標(biāo)準(zhǔn) LMS 算法的四個(gè)性能:一、收斂性;二、收斂速度;三、穩(wěn)態(tài)誤差;四、計(jì)算復(fù) 雜度。 只有在輸入信號(hào)具有嚴(yán)格穩(wěn)定的統(tǒng)計(jì)特性時(shí),權(quán)向量的優(yōu)解是不變的。否則, 將會(huì)隨著統(tǒng)計(jì)特性的變化而變化。自適應(yīng)算法則能夠通過(guò)不斷的調(diào)整濾波器權(quán)向量,使權(quán)向量接近優(yōu)解 。因此,自適應(yīng)算法在平穩(wěn)條件下的性能表現(xiàn)可以認(rèn)為是非平穩(wěn)條件下的一種特殊情況。如果在平穩(wěn)條件下,自適應(yīng)算法能夠快 速,平穩(wěn)的逼近權(quán)向量的優(yōu)值,那么在非平穩(wěn)條件下,該算法也能很好的逼近時(shí)變的 權(quán)向量?jī)?yōu)解。
五、算法流程
下面介紹一下LMS算法的基本流程。
1. 初始化工作,為各個(gè)輸入端的權(quán)值覆上隨機(jī)初始值;
2. 隨機(jī)挑選一組訓(xùn)練數(shù)據(jù),進(jìn)行計(jì)算得出計(jì)算結(jié)構(gòu)C;
3. 利用公式3對(duì)每一個(gè)輸入端的權(quán)值進(jìn)行調(diào)整;
4. 利用公式1計(jì)算出均方差MSE;
5. 對(duì)均方差進(jìn)行判斷,如果大于某一個(gè)給定值,回到步驟2,繼續(xù)算法;如果小于給定值,就輸出正確權(quán)值,并結(jié)束算法。
六、算法實(shí)現(xiàn)
以下就給出一段LMS算法的代碼。
[cpp] view plain copyconst unsigned int nTests =4;
const unsigned int nInputs =2;
const double rho =0.005;
struct lms_testdata
{
doubleinputs[nInputs];
doubleoutput;
};
double compute_output(constdouble * inputs,double* weights)
{
double sum =0.0;
for (int i = 0 ; i 《 nInputs; ++i)
{
sum += weights[i]*inputs[i];
}
//bias
sum += weights[nInputs]*1.0;
return sum;
}
//計(jì)算均方差
double caculate_mse(constlms_testdata * testdata,double * weights)
{
double sum =0.0;
for (int i = 0 ; i 《 nTests ; ++i)
{
sum += pow(testdata[i].output -compute_output(testdata[i].inputs,weights),2);
}
return sum/(double)nTests;
}
//對(duì)計(jì)算所得值,進(jìn)行分類
int classify_output(doubleoutput)
{
if(output》 0.0)
return1;
else
return-1;
}
int _tmain(int argc,_TCHAR* argv[])
{
lms_testdata testdata[nTests] = {
{-1.0,-1.0, -1.0},
{-1.0, 1.0, -1.0},
{ 1.0,-1.0, -1.0},
{ 1.0, 1.0, 1.0}
};
doubleweights[nInputs + 1] = {0.0};
while(caculate_mse(testdata,weights)》 0.26)//計(jì)算均方差,如果大于給定值,算法繼續(xù)
{
intiTest = rand()%nTests;//隨機(jī)選擇一組數(shù)據(jù)
doubleoutput = compute_output(testdata[iTest].inputs,weights);
doubleerr = testdata[iTest].output - output;
//調(diào)整輸入端的權(quán)值
for (int i = 0 ; i 《 nInputs ; ++i)
{
weights[i] = weights[i] + rho * err* testdata[iTest].inputs[i];
}
weights[nInputs] = weights[nInputs] +rho * err;
cout《《“mse:”《《caculate_mse(testdata,weights)《《endl;
}
for(int w = 0 ; w 《 nInputs + 1 ; ++w)
{
cout《《“weight”《《w《《“:”《《weights[w]《《endl;
}
cout《《“\n”;
for (int i = 0 ;i 《 nTests ; ++i)
{
cout《《“rightresult:êo”《《testdata[i].output《《“\t”;
cout《《“caculateresult:” 《《 classify_output(compute_output(testdata[i].inputs,weights))《《endl;
}
//
char temp ;
cin》》temp;
return 0;
}
 電子發(fā)燒友App
電子發(fā)燒友App










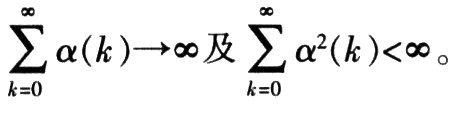
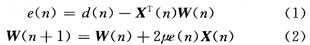
















評(píng)論