哈夫曼樹中的名詞意思

　　樹的權(quán)值：每個(gè)樹節(jié)點(diǎn)所在的那個(gè)數(shù)字。

　　路徑：兩個(gè)節(jié)點(diǎn)之間所經(jīng)過的分支。

　　路徑長度： 某一路徑上的分支條數(shù)。

　　節(jié)點(diǎn)帶權(quán)路徑長度： 節(jié)點(diǎn)的權(quán)值*該節(jié)點(diǎn)的路徑長度。

　　樹帶權(quán)路徑長度：所有葉子節(jié)點(diǎn)的帶全路徑長度之和。

　　樹帶權(quán)路徑長度：所有葉子節(jié)點(diǎn)的帶全路徑長度之和。

　　1、基本概念

　　a、路徑和路徑長度

　　若在一棵樹中存在著一個(gè)結(jié)點(diǎn)序列 k1，k2，……，kj， 使得 ki是ki+1 的雙親（1《=i《j），則稱此結(jié)點(diǎn)序列是從 k1 到 kj 的路徑。

　　從 k1 到 kj 所經(jīng)過的分支數(shù)稱為這兩點(diǎn)之間的路徑長度，它等于路徑上的結(jié)點(diǎn)數(shù)減1.

　　b、結(jié)點(diǎn)的權(quán)和帶權(quán)路徑長度

　　在許多應(yīng)用中，常常將樹中的結(jié)點(diǎn)賦予一個(gè)有著某種意義的實(shí)數(shù)，我們稱此實(shí)數(shù)為該結(jié)點(diǎn)的權(quán)，（如下面一個(gè)樹中的藍(lán)色數(shù)字表示結(jié)點(diǎn)的權(quán)）

　　結(jié)點(diǎn)的帶權(quán)路徑長度規(guī)定為從樹根結(jié)點(diǎn)到該結(jié)點(diǎn)之間的路徑長度與該結(jié)點(diǎn)上權(quán)的乘積。

　　c、樹的帶權(quán)路徑長度

　　樹的帶權(quán)路徑長度定義為樹中所有葉子結(jié)點(diǎn)的帶權(quán)路徑長度之和，公式為：

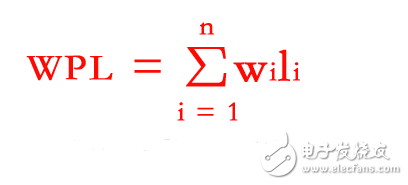
　　其中，n表示葉子結(jié)點(diǎn)的數(shù)目，wi 和 li 分別表示葉子結(jié)點(diǎn) ki 的權(quán)值和樹根結(jié)點(diǎn)到 ki 之間的路徑長度。

　　如下圖中樹的帶權(quán)路徑長度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4 = 122

　　d、哈夫曼樹

　　哈夫曼樹又稱最優(yōu)二叉樹。它是 n 個(gè)帶權(quán)葉子結(jié)點(diǎn)構(gòu)成的所有二叉樹中，帶權(quán)路徑長度 WPL 最小的二叉樹。

　　如下圖為一哈夫曼樹示意圖。

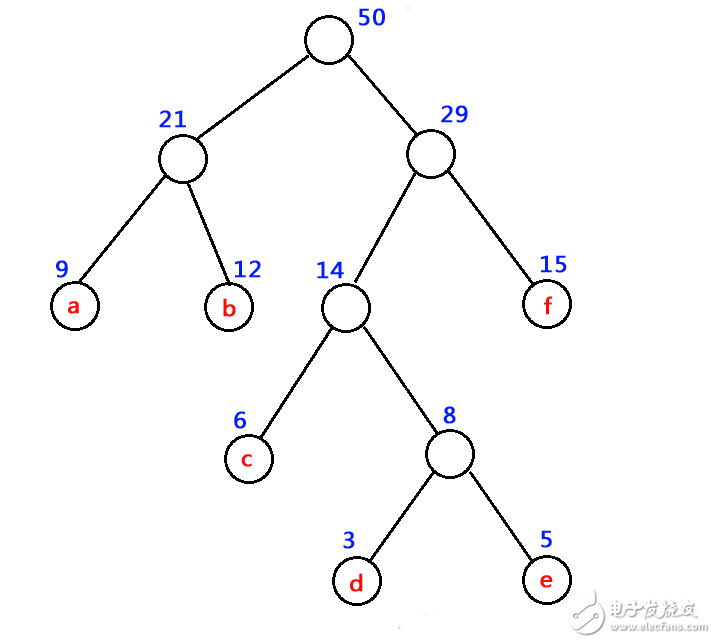
　　哈夫曼樹的構(gòu)造

　　根據(jù)哈弗曼樹的定義，一棵二叉樹要使其WPL值最小，必須使權(quán)值越大的葉子結(jié)點(diǎn)越靠近根結(jié)點(diǎn)，而權(quán)值越小的葉子結(jié)點(diǎn)越遠(yuǎn)離根結(jié)點(diǎn)。

　　哈弗曼依據(jù)這一特點(diǎn)提出了一種構(gòu)造最優(yōu)二叉樹的方法，其基本思想如下：

　　下面演示了用Huffman算法構(gòu)造一棵Huffman樹的過程：

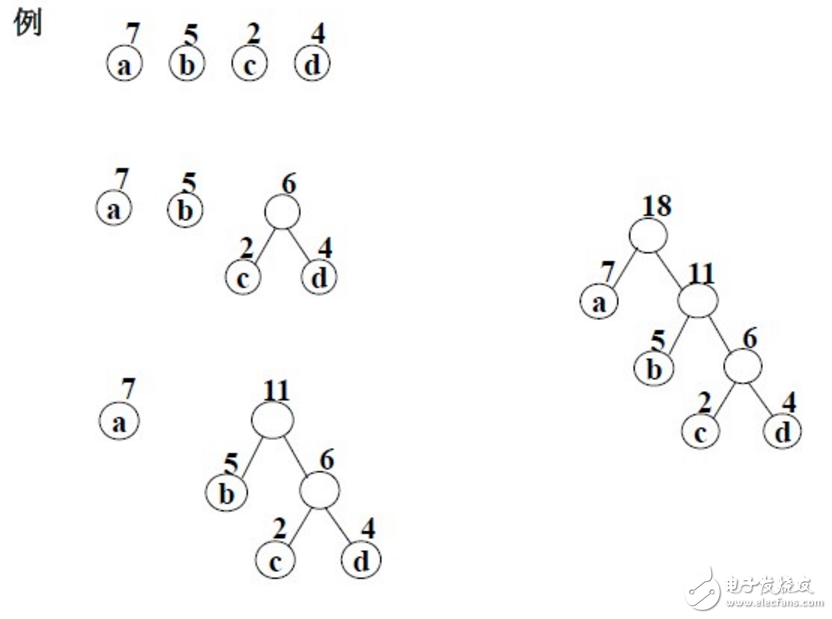
　　假設(shè)有n個(gè)權(quán)值，則構(gòu)造出的哈夫曼樹有n個(gè)葉子結(jié)點(diǎn)。 n個(gè)權(quán)值分別設(shè)為 w1、w2、…、wn，則哈夫曼樹的構(gòu)造規(guī)則為：

　　（1） 將w1、w2、…，wn看成是有n 棵樹的森林（每棵樹僅有一個(gè)結(jié)點(diǎn)）；

　　（2） 在森林中選出兩個(gè)根結(jié)點(diǎn)的權(quán)值最小的樹合并，作為一棵新樹的左、右子樹，且新樹的根結(jié)點(diǎn)權(quán)值為其左、右子樹根結(jié)點(diǎn)權(quán)值之和；

　　（3）從森林中刪除選取的兩棵樹，并將新樹加入森林；

　　（4）重復(fù)（2）、（3）步，直到森林中只剩一棵樹為止，該樹即為所求得的哈夫曼樹。

　　如：對 下圖中的六個(gè)帶權(quán)葉子結(jié)點(diǎn)來構(gòu)造一棵哈夫曼樹，步驟如下：

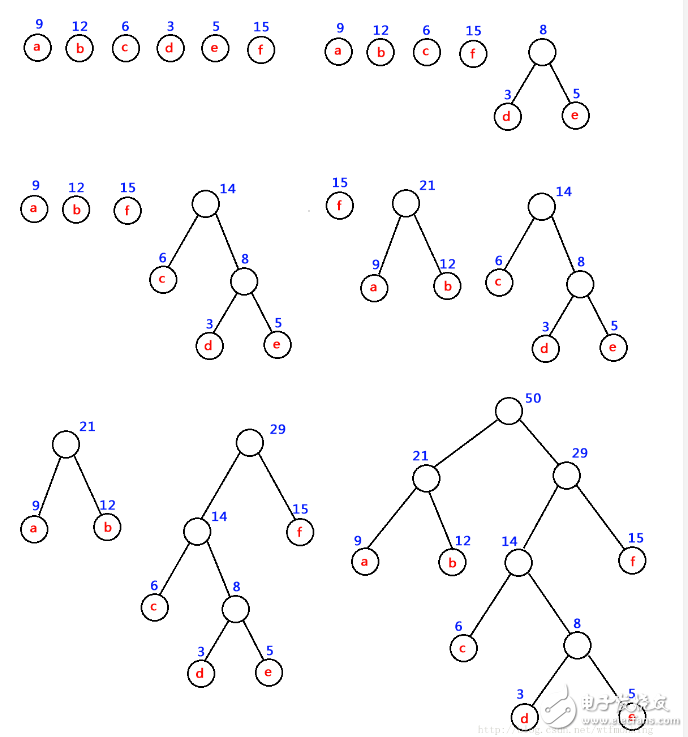
　　注意：為了使得到的哈夫曼樹的結(jié)構(gòu)盡量唯一，通常規(guī)定生成的哈夫曼樹中每個(gè)結(jié)點(diǎn)的左子樹根結(jié)點(diǎn)的權(quán)小于等于右子樹根結(jié)點(diǎn)的權(quán)。

　　具體算法如下：

　　//2、根據(jù)數(shù)組 a 中 n 個(gè)權(quán)值建立一棵哈夫曼樹，返回樹根指針

　　struct BTreeNode* CreateHuffman（ElemType a［］， int n）

　　{

　　int i， j;

　　struct BTreeNode **b， *q;

　　b = malloc（n*sizeof（struct BTreeNode））;

　　for （i = 0; i 《 n; i++） //初始化b指針數(shù)組，使每個(gè)指針元素指向a數(shù)組中對應(yīng)的元素結(jié)點(diǎn)

　　{

　　b［i］ = malloc（sizeof（struct BTreeNode））;

　　b［i］-》data = a［i］;

　　b［i］-》left = b［i］-》right = NULL;

　　}

　　for （i = 1; i 《 n; i++）//進(jìn)行 n-1 次循環(huán)建立哈夫曼樹

　　{

　　//k1表示森林中具有最小權(quán)值的樹根結(jié)點(diǎn)的下標(biāo)，k2為次最小的下標(biāo)

　　int k1 = -1， k2;

　　for （j = 0; j 《 n; j++）//讓k1初始指向森林中第一棵樹，k2指向第二棵

　　{

　　if （b［j］ ！= NULL && k1 == -1）

　　{

　　k1 = j;

　　continue;

　　}

　　if （b［j］ ！= NULL）

　　{

　　k2 = j;

　　break;

　　}

　　}

　　for （j = k2; j 《 n; j++）//從當(dāng)前森林中求出最小權(quán)值樹和次最小

　　{

　　if （b［j］ ！= NULL）

　　{

　　if （b［j］-》data 《 b［k1］-》data）

　　{

　　k2 = k1;

　　k1 = j;

　　}

　　else if （b［j］-》data 《 b［k2］-》data）

　　k2 = j;

　　}

　　}

　　//由最小權(quán)值樹和次最小權(quán)值樹建立一棵新樹，q指向樹根結(jié)點(diǎn)

　　q = malloc（sizeof（struct BTreeNode））;

　　q-》data = b［k1］-》data + b［k2］-》data;

　　q-》left = b［k1］;

　　q-》right = b［k2］;

　　b［k1］ = q;//將指向新樹的指針賦給b指針數(shù)組中k1位置

　　b［k2］ = NULL;//k2位置為空

　　}

　　free（b）; //刪除動(dòng)態(tài)建立的數(shù)組b

　　return q; //返回整個(gè)哈夫曼樹的樹根指針

　　}

　　哈夫曼樹的在編碼中的應(yīng)用

　　在電文傳輸中，需要將電文中出現(xiàn)的每個(gè)字符進(jìn)行二進(jìn)制編碼。在設(shè)計(jì)編碼時(shí)需要遵守兩個(gè)原則：

　　（1）發(fā)送方傳輸?shù)亩M(jìn)制編碼，到接收方解碼后必須具有唯一性，即解碼結(jié)果與發(fā)送方發(fā)送的電文完全一樣；

　　（2）發(fā)送的二進(jìn)制編碼盡可能地短。下面我們介紹兩種編碼的方式。

　　1. 等長編碼

　　這種編碼方式的特點(diǎn)是每個(gè)字符的編碼長度相同（編碼長度就是每個(gè)編碼所含的二進(jìn)制位數(shù)）。假設(shè)字符集只含有4個(gè)字符A，B，C，D，用二進(jìn)制兩位表示的編碼分別為00，01，10，11。若現(xiàn)在有一段電文為：ABACCDA，則應(yīng)發(fā)送二進(jìn)制序列：00010010101100，總長度為14位。當(dāng)接收方接收到這段電文后，將按兩位一段進(jìn)行譯碼。這種編碼的特點(diǎn)是譯碼簡單且具有唯一性，但編碼長度并不是最短的。

　　2. 不等長編碼

　　在傳送電文時(shí)，為了使其二進(jìn)制位數(shù)盡可能地少，可以將每個(gè)字符的編碼設(shè)計(jì)為不等長的，使用頻度較高的字符分配一個(gè)相對比較短的編碼，使用頻度較低的字符分配一個(gè)比較長的編碼。例如，可以為A，B，C，D四個(gè)字符分別分配0，00，1，01，并可將上述電文用二進(jìn)制序列：000011010發(fā)送，其長度只有9個(gè)二進(jìn)制位，但隨之帶來了一個(gè)問題，接收方接到這段電文后無法進(jìn)行譯碼，因?yàn)闊o法斷定前面4個(gè)0是4個(gè)A，1個(gè)B、2個(gè)A，還是2個(gè)B，即譯碼不唯一，因此這種編碼方法不可使用。

　　因此，為了設(shè)計(jì)長短不等的編碼，以便減少電文的總長，還必須考慮編碼的唯一性，即在建立不等長編碼時(shí)必須使任何一個(gè)字符的編碼都不是另一個(gè)字符的前綴，這宗編碼稱為前綴編碼（prefix code）

　　（1）利用字符集中每個(gè)字符的使用頻率作為權(quán)值構(gòu)造一個(gè)哈夫曼樹；

　　（2）從根結(jié)點(diǎn)開始，為到每個(gè)葉子結(jié)點(diǎn)路徑上的左分支賦予0，右分支賦予1，并從根到葉子方向形成該葉子結(jié)點(diǎn)的編碼

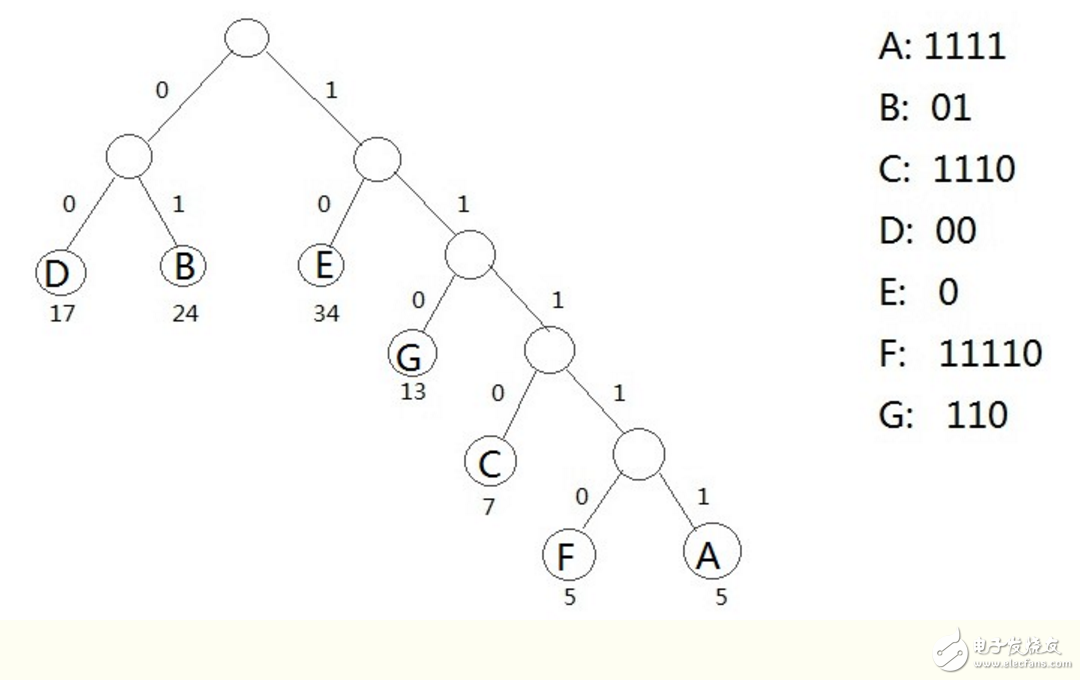
　　例題：

　　假設(shè)一個(gè)文本文件TFile中只包含7個(gè)字符{A，B，C，D，E，F(xiàn)，G}，這7個(gè)字符在文本中出現(xiàn)的次數(shù)為{5，24，7，17，34，5，13}

　　利用哈夫曼樹可以為文件TFile構(gòu)造出符合前綴編碼要求的不等長編碼

　　具體做法：

　　1. 將TFile中7個(gè)字符都作為葉子結(jié)點(diǎn)，每個(gè)字符出現(xiàn)次數(shù)作為該葉子結(jié)點(diǎn)的權(quán)值

　　2. 規(guī)定哈夫曼樹中所有左分支表示字符0，所有右分支表示字符1，將依次從根結(jié)點(diǎn)到每個(gè)葉子結(jié)點(diǎn)所經(jīng)過的分支的二進(jìn)制位的序列作為該

　　結(jié)點(diǎn)對應(yīng)的字符編碼

　　3. 由于從根結(jié)點(diǎn)到任何一個(gè)葉子結(jié)點(diǎn)都不可能經(jīng)過其他葉子，這種編碼一定是前綴編碼，哈夫曼樹的帶權(quán)路徑長度正好是文件TFile編碼的總長度

　　通過哈夫曼樹來構(gòu)造的編碼稱為哈弗曼編碼（huffman code）