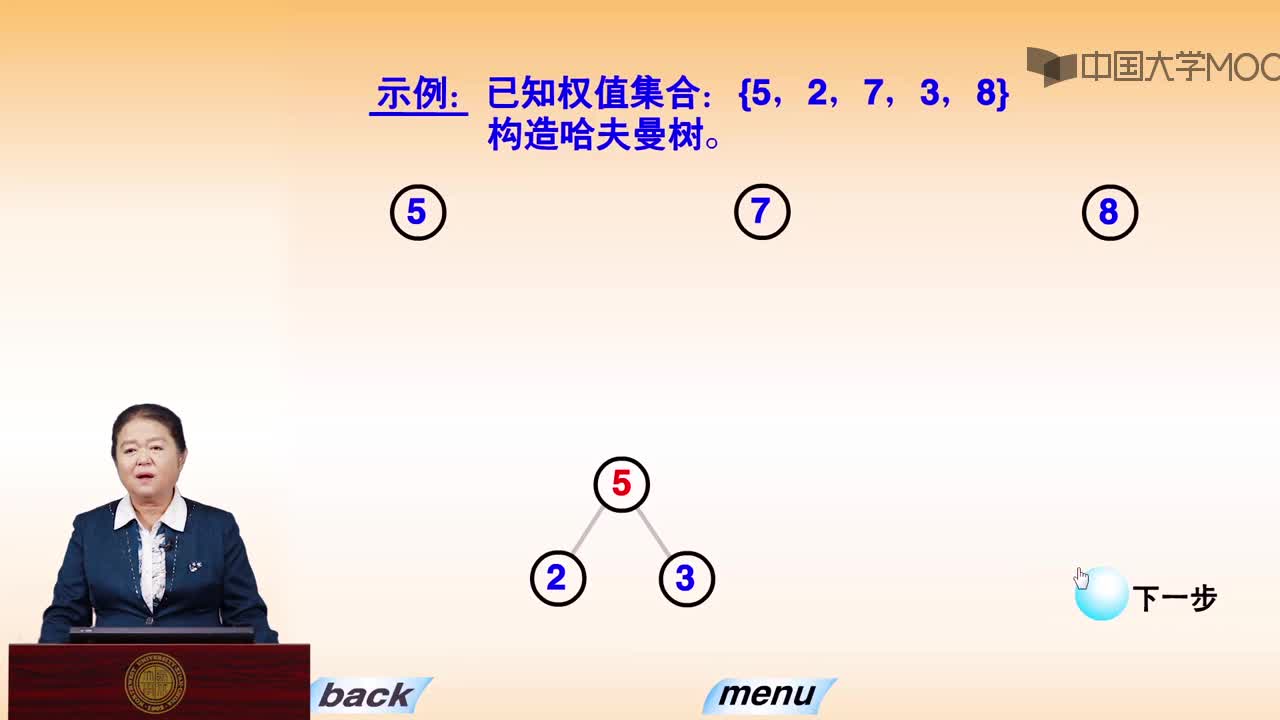
哈夫曼樹的帶權路徑長度是什么？

　　1．樹的路徑長度

　　樹的路徑長度是從樹根到樹中每一結點的路徑長度之和。在結點數目相同的二叉樹中，完全二叉樹的路徑長度最短。

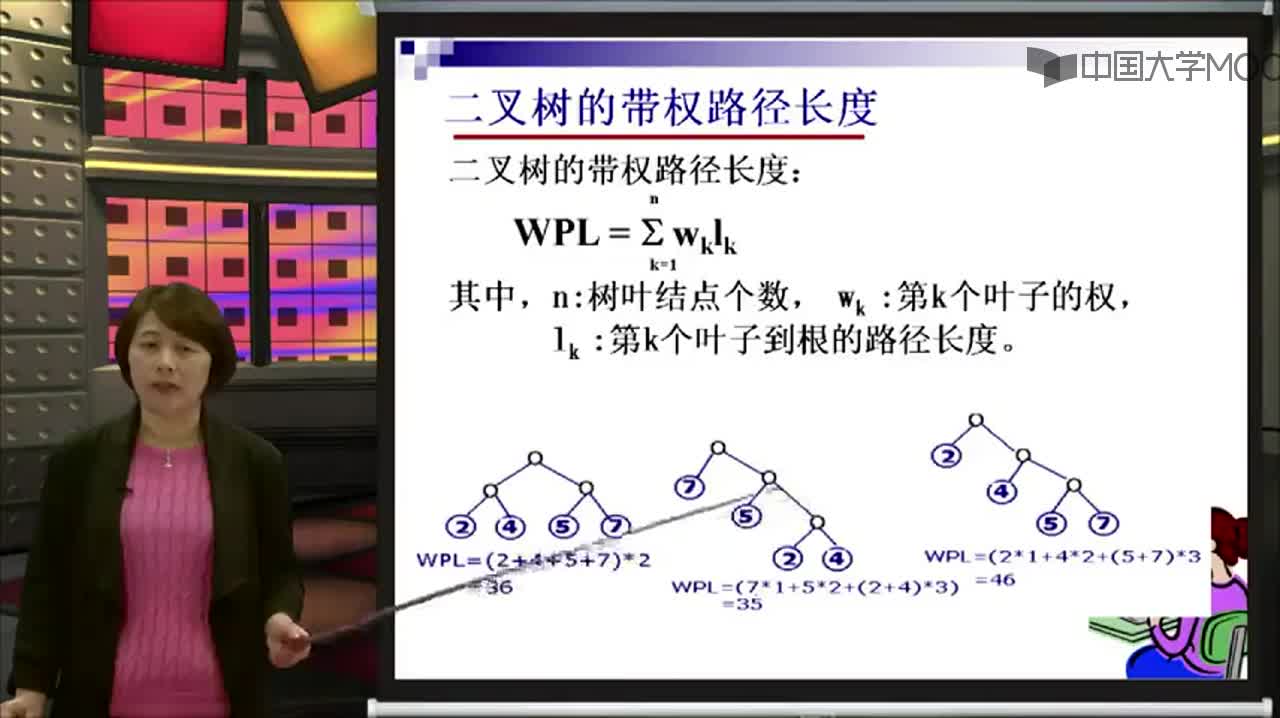
　　2．樹的帶權路徑長度（Weighted Path Length of Tree，簡記為WPL）

　　結點的權：在一些應用中，賦予樹中結點的一個有某種意義的實數。

　　結點的帶權路徑長度：結點到樹根之間的路徑長度與該結點上權的乘積。

　　樹的帶權路徑長度（Weighted Path Length of Tree）：定義為樹中所有葉結點的帶權路徑長度之和，通常記為：

　　其中：

　　n表示葉子結點的數目

　　wi和li分別表示葉結點ki的權值和根到結點ki之間的路徑長度。

　　樹的帶權路徑長度亦稱為樹的代價。

　　3．最優二叉樹或哈夫曼樹

　　在權為wl，w2，…，wn的n個葉子所構成的所有二叉樹中，帶權路徑長度最小（即代價最小）的二叉樹稱為最優二叉樹或哈夫曼樹。

　　【例】給定4個葉子結點a，b，c和d，分別帶權7，5，2和4.構造如下圖所示的三棵二叉樹（還有許多棵），它們的帶權路徑長度分別為：

　　（a）WPL=7*2+5*2+2*2+4*2=36

　　（b）WPL=7*3+5*3+2*1+4*2=46

　　（c）WPL=7*1+5*2+2*3+4*3=35

　　其中（c）樹的WPL最小，可以驗證，它就是哈夫曼樹。

　　注意：

　　① 葉子上的權值均相同時，完全二叉樹一定是最優二叉樹，否則完全二叉樹不一定是最優二叉樹。

　　② 最優二叉樹中，權越大的葉子離根越近。

　　③ 最優二叉樹的形態不唯一，WPL最小

　　怎么求哈夫曼的帶權路徑長度

　　【問題描述】

　　已知輸入兩行正整數，第二行正整數之間用空格鍵分開，請建立一個哈夫曼樹，以輸入的數字為葉節點，求這棵哈夫曼樹的帶權路徑長度。

　　【輸入形式】

　　首先第一行為輸入正整數的個數，然后接下來的一行正整數，代表葉結點，正整數個數不超過1000個

　　【輸出形式】

　　輸出相應的權值

　　【樣例輸入】

　　5

　　4 5 6 7 8

　　【樣例輸出】

　　69

　　關于哈夫曼樹——

　　1、 路徑長度

　　從樹中一個結點到另一個結點之間的分支構成兩個結點之間的路徑，路徑上的分支數目稱做路徑長度。

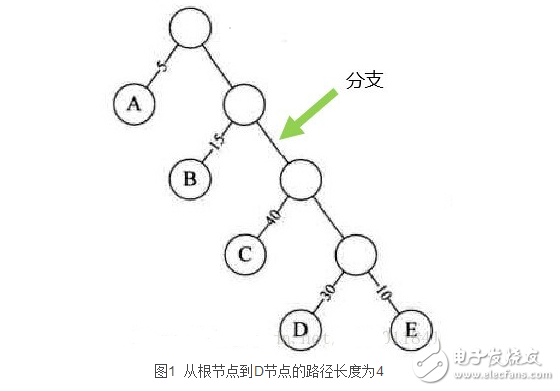
　　1、 樹的路徑長度

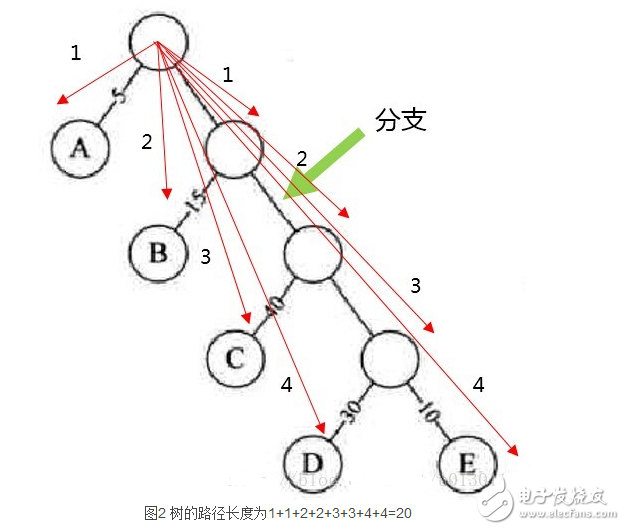
　　路徑長度就是從樹根到每一結點的路徑長度之和。

　　1、 哈夫曼樹：

　　帶權路徑長度WPL（Weighted Path Length）最小的二叉樹，也稱為最優二又樹。

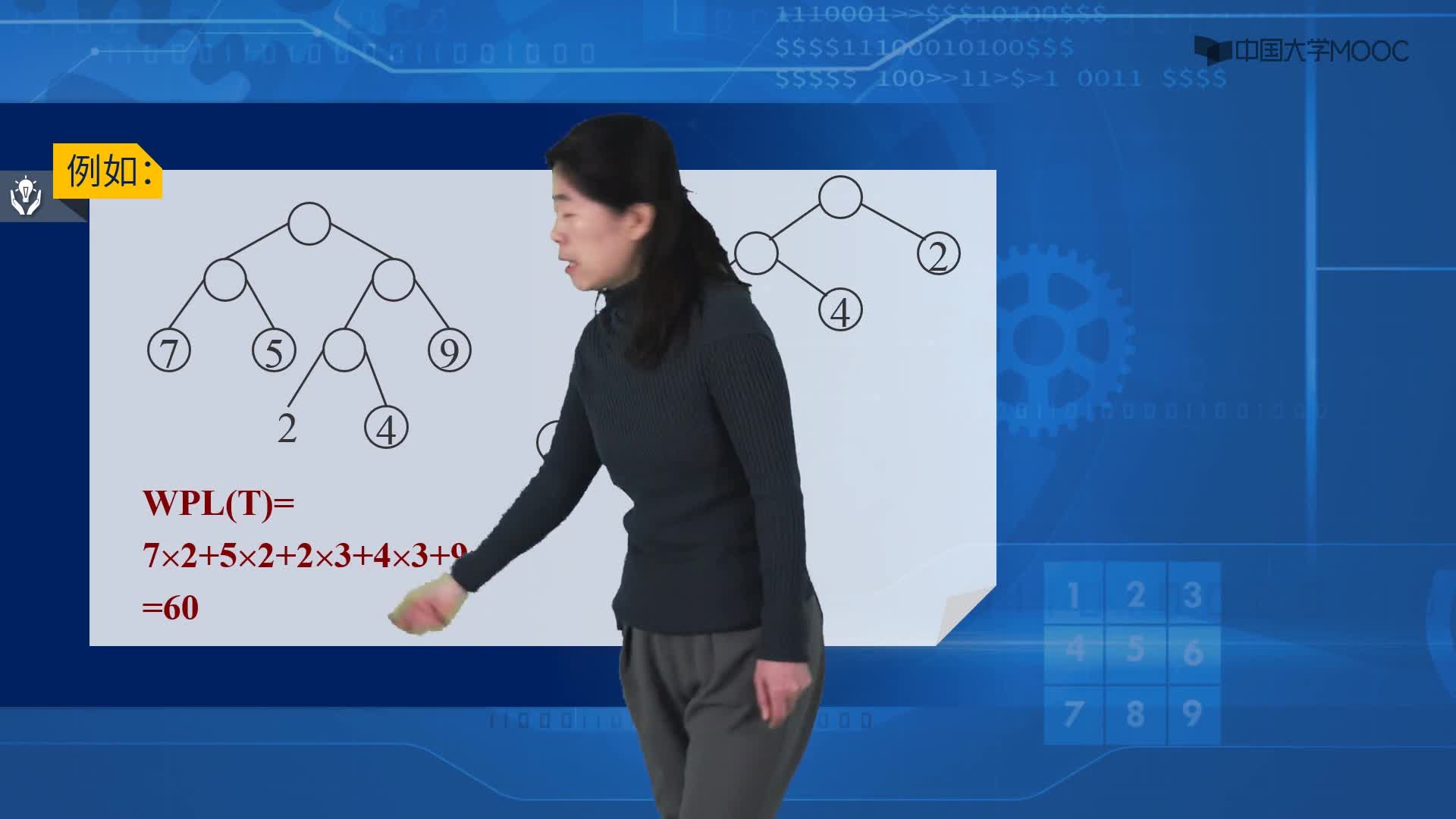
　　例： 上圖的WPL=1*5 + 2*15 + 3*40 + 4*30 + 4*10= 315

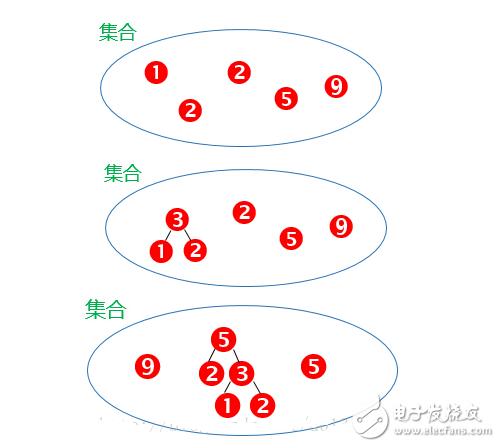
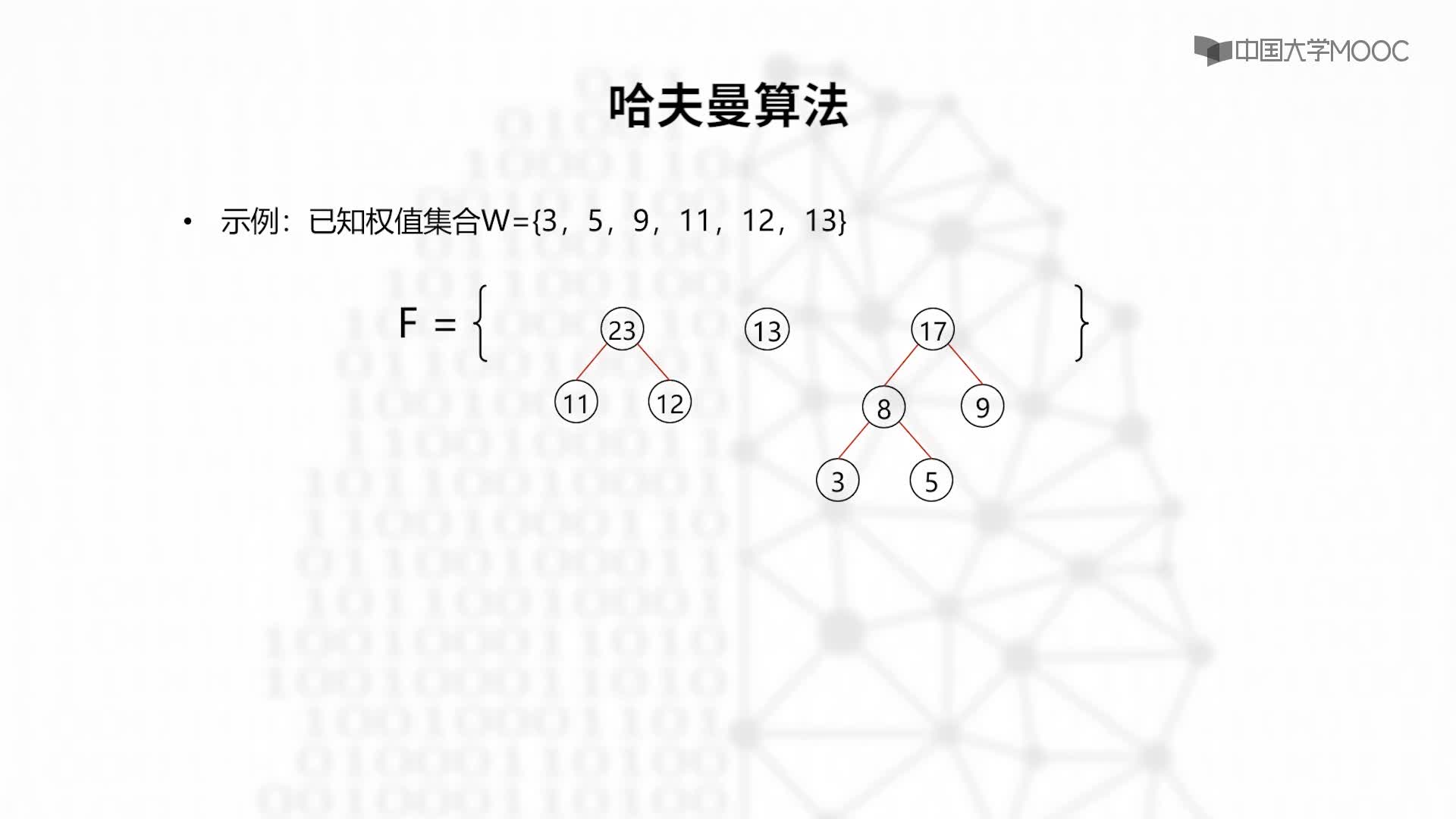
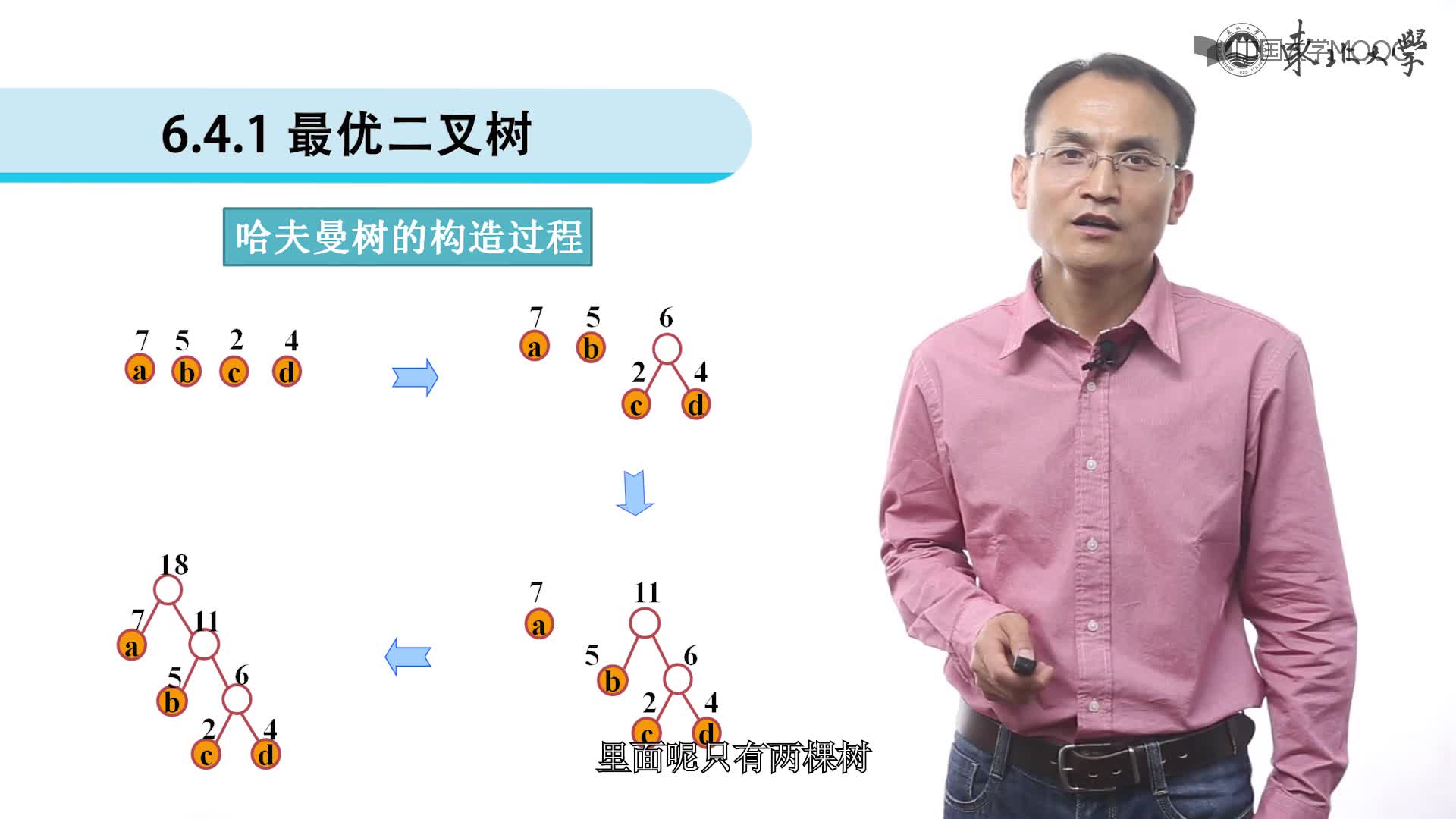
　　先了解通過剛才的步驟，我們可以得出構造哈夫曼樹的算法描述。

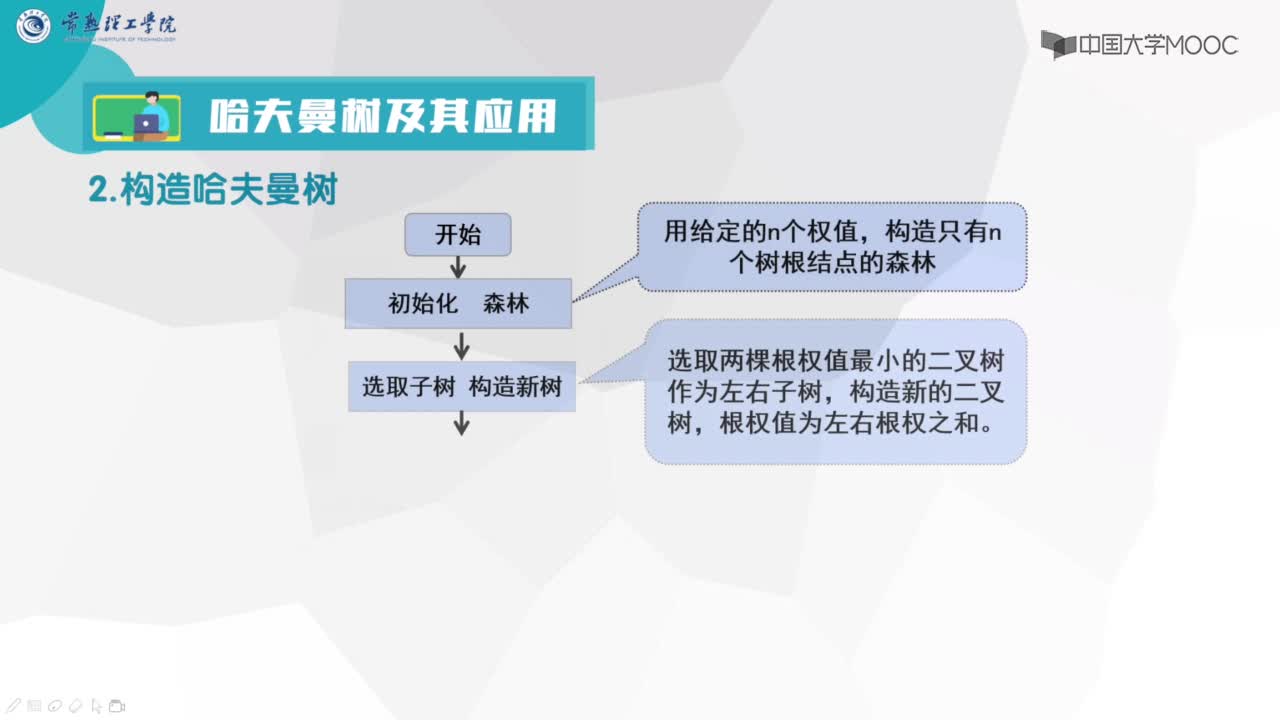
　　1、根據給定的n個權值{w［1］，w［2］，…，w［n］}構成n棵二叉樹的集合F={T［1］，T［2］，…T［n］}， 其中每棵二叉樹T［i］;中只有一個帶權為w［i］的根結點，其左右子樹均為空。

　　2、在F中選取兩棵根結點的權值最小的樹作為左右子樹構造一棵新的。二叉樹，且置新的二叉樹的根結點的權值為其左右子樹上根結點的權值之和，

　　3、在F中刪除這兩棵樹，同時將新得到的二義樹加入F中。

　　4重復2和3步驟，直到F只含一棵樹為止。這棵樹便是哈夫曼樹。

　　結合例題說明一下這個算法

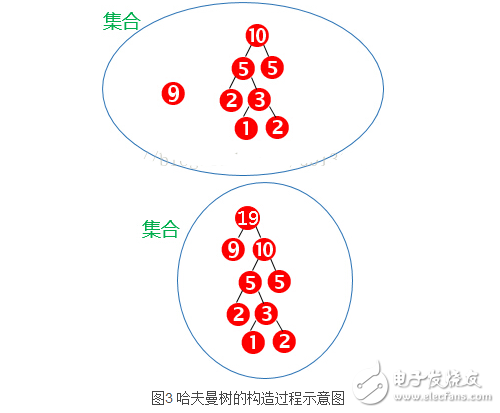
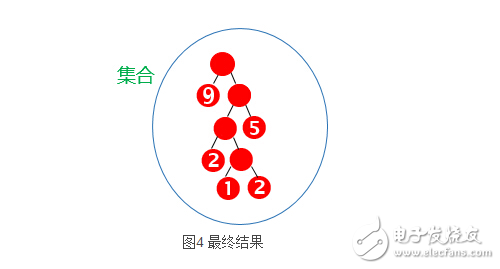
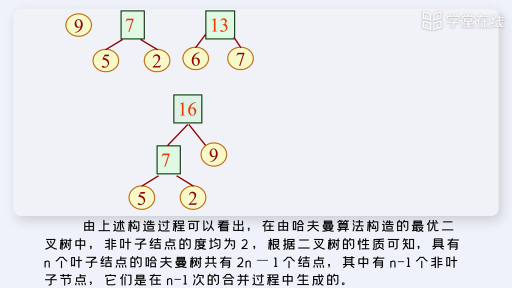
　　那么可以由上面的哈夫曼樹計算出最小帶權路徑長度

　　WPL = 1*9 + 2*5 + 3*2 + 4*1 + 4*2 =37

　　另外還可以有另外一個方法，結合算法描述仔細觀察發現最小帶權路徑長度為非葉子結點的和 ，即

　　WPL= 19 + 10 +5 +3=37

　　至于算法的正確性，一下子也想不到什么好的辦法來證明，不過應該是可以邏輯推導過來的。

　　那么要實現這段程序，由上面的算法描述圖我們已經知道差不多了，主要分為三步：

　　一、排序，直到數組中只有一個數則退出

　　二、最小兩個數加起來，即為非葉子節點，累加到累加器中

　　三、把最小兩個數加起來作為一個新的值保存在數組中，去掉最小兩個值，跳回第一步

　　#include《stdio.h》

　　#include《stdlib.h》 //qsort（）;

　　#define N 1010

　　int rising（const void *a， const void *b）

　　{

　　return *（int*）a - *（int*）b;

　　}

　　int main（）

　　{

　　int leaf［N］ = {0}， n， i， sum = 0;

　　scanf（“%d”， &n）;

　　for（i=0; i《n; i++）

　　scanf（“%d”， leaf+i）;

　　for（i=0; i《n-1; i++）

　　{

　　qsort（leaf+i， n-i， sizeof（leaf［0］）， rising）; //排序并剔除已使用的葉結點

　　leaf［i+1］ += leaf［i］; //合并兩個最小的葉結點成一新的節點（放在leaf［i+1］中）

　　sum += leaf［i+1］; //總路徑長 = 所有非葉結點之和

　　}

　　printf（“%d\n”， sum）;

　　return 0;

　　}