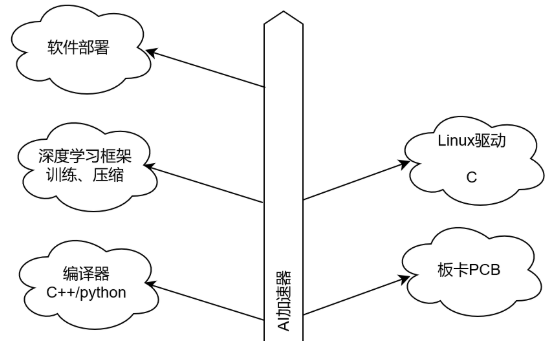
作者注記
我是2017年11月開始接觸深度學習,至今剛好五年。2019年10月入職上海交大,至今三年,剛好第一階段考核。2022年8月19號,我在第一屆中國機器學習與科學應用大會做大會報告,總結這五年的研究以及展望未來的方向。本文是該報告里關于理論方面的研究總結(做了一點擴展)。
我理解的深度學習
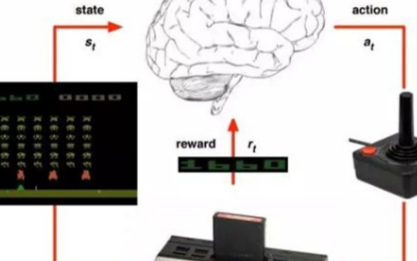
我原本是研究計算神經科學的,研究的內容,宏觀來講是從數學的角度理解大腦工作的原理,具體來說,我的研究是處理高維的神經元網絡產生的脈沖數據,嘗試去理解這些信號是如何處理輸入的信號。但大腦過于復雜,維度也過于高,我們普通大腦有一千億左右個神經元,每個神經元還和成千上萬個其它神經元有信號傳遞,我對處理這類數據并沒有太多信心,那階段也剛好讀到一篇文章,大意是把現階段計算神經科學的研究方法用來研究計算機的芯片,結論是這些方法并不能幫助我們理解芯片的工作原理。另一個讓我覺得非常難受的地方是我們不僅對大腦了解很少,還非常難以獲得大腦的數據。于是,我們當時思考,能否尋找一個簡單的網絡模型,能夠實現復雜的功能,同時我們對它的理解也很少的例子,我們通過研究它來啟發我們對大腦的研究。
當時是2017年底,深度學習已經非常流行,特別是我的同學已經接觸深度學習一段時間,所以我們迅速了解到深度學習。其結構和訓練看起來足夠簡單,但能力不凡,而且與其相關的理論正處在萌芽階段。因此,我進入深度學習的第一個想法是把它當作研究大腦的簡單模型。?顯然,在這種“類腦研究”的定位下,我們關心的是深度學習的基礎研究。這里,我想區分深度學習的“理論”和“基礎研究”。我認為“理論”給人一種全是公式和證明的感覺。而“基礎研究”的范圍聽起來會更廣闊一些,它不僅可以包括“理論”,還可以是一些重要的現象,直觀的解釋,定律,經驗原則等等。這種區分只是一種感性的區分,實際上,我們在談論它們的時候,并不真正做這么細致的區分。盡管是以深度學習為模型,來研究大腦為何會有如此復雜的學習能力,但大腦和深度學習還是有明顯的差異。而我從知識儲備、能力和時間上來看,都很難同時在這兩個目前看起來距離仍然很大的領域同時深入。
于是我選擇全面轉向深度學習,研究的問題是,深度學習作為一個算法,它有什么樣的特征。“沒有免費的午餐”的定理告訴我們,當考慮所有可能的數據集的平均性能時,所有算法都是等價的,也就是沒有哪一種算法是萬能的。我們需要厘清深度學習這類算法適用于什么數據,以及不適用于什么數據。?事實上,深度學習理論并不是處于萌芽階段,從上世紀中葉,它剛開始發展的時候,相關的理論就已經開始了,也有過一些重要的結果,但整體上來說,它仍然處于初級階段。對我而言,這更是一個非常困難的問題。于是,我轉而把深度學習當作一種“玩具”,通過調整各類超參數和不同的任務,觀察它會產生哪些“自然現象”。設定的目標也不再高大上,而是有趣即可,發現有趣的現象,然后解釋它,也許還可以用它來指導實際應用。在上面這些認識下,我們從深度神經網絡訓練中的一些有趣的現象開始。于我個人,我是從頭開始學習寫python和tensorflow,更具體是,從網上找了幾份代碼,邊抄邊理解。
神經網絡真的很復雜嗎?
在傳統的學習理論中,模型的參數量是指示模型復雜程度很重要的一個指標。當模型的復雜度增加時,模型擬合訓練數據的能力會增強,但也會帶來在測試集上過擬合的問題。馮·諾依曼曾經說過一句著名的話,給我四個參數,我能擬合一頭大象,五個參數可以讓大象的鼻子動起來。
因此,傳統建模相關的研究人員在使用神經網絡時,經常會計算模型參數量,以及為了避免過擬合,刻意用參數少的網絡。然而,今天神經網絡能夠大獲成功,一個重要的原因正是使用了超大規模的網絡。網絡的參數數量往往遠大于樣本的數量,但卻不像傳統學習理論所預言的那樣過擬合。這便是這些年受到極大關注的泛化迷團。實際上,在1995年,Leo Breiman在一篇文章中就已經指出了這個問題。在神經網絡非常流行和重要的今天,這個迷團愈加重要。我們可以問:帶有大量參數的神經網絡真的很復雜嗎?
答案是肯定的!上世紀八十年代末的理論工作證明當兩層神經網絡(激活函數非多項式函數)足夠寬時,它可以以任意精度逼近任意連續函數,這也就是著名的“萬有逼近”定理。實際上,我們應該問一個更加有意義的問題:在實際訓練中,神經網絡真的很復雜嗎??逼近論證明的解在實際訓練中幾乎不可能遇到。實際的訓練,需要設定初始值、優化算法、網絡結構等超參數。對我們實際要有指導作用,我們就不能脫離這些因素來考慮泛化的問題,因為泛化本身就是依賴實際數據的問題。

兩種簡單偏好的現象
在學習與訓練神經網絡的過程中,我們很容易發現,神經網絡的訓練有一定的規律。在我們的研究中,有兩種現象很有趣,在研究和解釋它們的過程中,我們發現它們同樣是很有意義的。我先簡單介紹,然后再詳細分別介紹。第一,我們發現神經網絡在擬合數據的過程中經常會先學習低頻,而后慢慢學習高頻。我們把這個現象命名為頻率原則(Frequency Principle, F-Principle)[1, 2],也有其它工作把它稱為Spectral bias。第二,我們發現在訓練過程,有很多神經元的輸入權重(向量)的方向會保持一致。我們稱之為凝聚現象。這些輸入權重一樣的神經元對輸入的處理是一樣的,那它們就可以簡化成一個神經元,也就是一個大網絡可以簡化成小網絡[3, 4]。這兩種現象都體現神經網絡在訓練過程中有一種隱式的簡單偏好,低頻偏好或者有效小網絡偏好。低頻偏好是非常普遍的,但小網絡偏好是要在非線性的訓練過程中才會出現的特征。
頻率原則
我早期在匯報頻率原則相關的工作的時候,做計算數學的老師同學非常有興趣,因為在傳統的迭代格式中,例如Jacobi迭代,低頻是收斂得非常慢的。多重網格方法非常有效地解決了這個問題。我們在實驗中,也驗證了神經網絡和Jacobi迭代在解PDE時完全不一樣的頻率收斂順序(如下圖)[2, 5]。
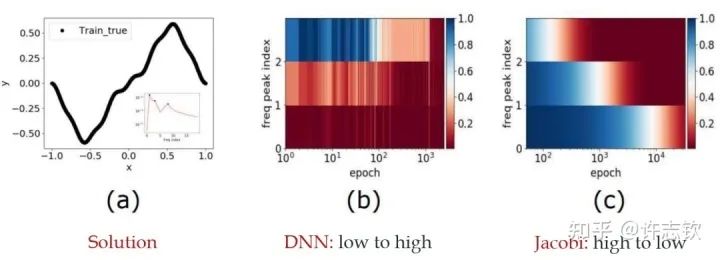
頻率原則有多廣泛呢??頻率原則最開始是在一維函數的擬合中發現的。我在調參的過程中發現神經網絡似乎總是先抓住目標函數的輪廓信息,然后再是細節。頻率是一種非常適合用來刻畫輪廓和細節的量。于是,我們在頻率空間看神經網絡的學習過程,發現非常明顯地從低頻到高頻的順序。
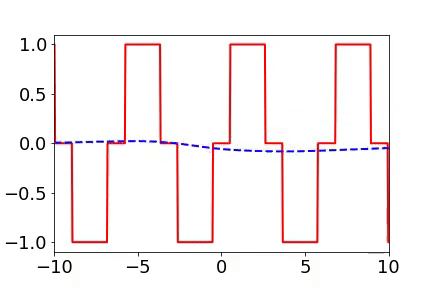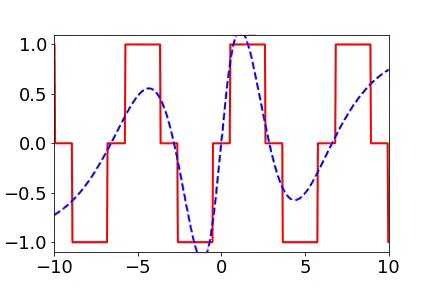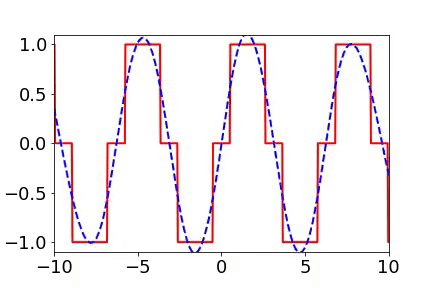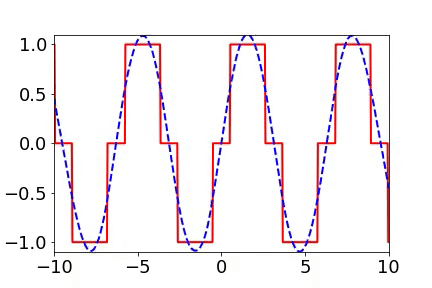 實域空間擬合(紅色為目標函數,藍色為DNN)
實域空間擬合(紅色為目標函數,藍色為DNN) 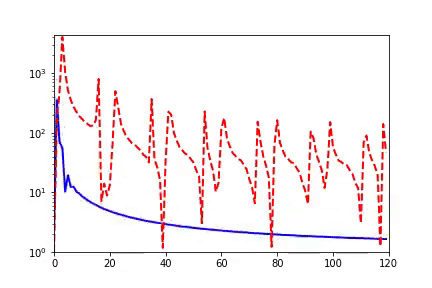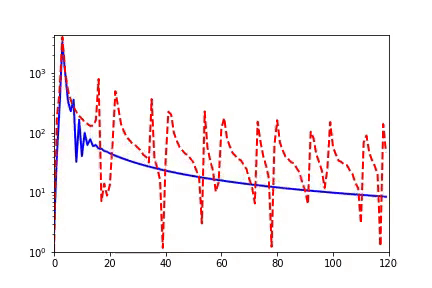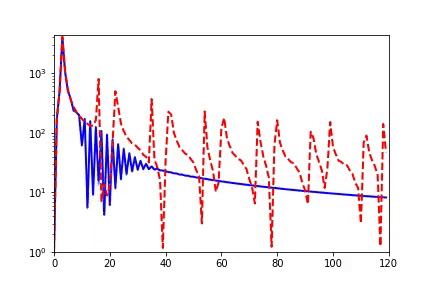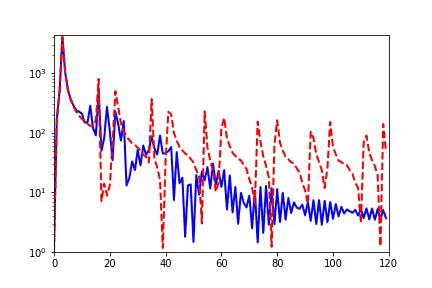 頻域空間擬合(紅色為目標函數,藍色為DNN)
頻域空間擬合(紅色為目標函數,藍色為DNN)
對于兩維的函數,以圖像為例,用神經網絡學習從兩維位置到灰度值的映射。神經網絡在訓練過程會慢慢記住更多細節。

對于更高維的例子,傅里葉變換是困難的,這也是不容易在高維的圖像分類任務中發現頻率原則的一個原因。我們的貢獻還有一點就是用一個例子論證針對簡單的低維問題的研究可以啟發深度學習的基礎研究。高維問題的頻率需要多說兩句。本質上,高頻指的是輸出對輸入的變化非常敏感。比如在圖片分類任務中,當一張圖片被修改一點點,輸出就發生變化。顯然,這說的正是對抗樣本。關于高維中驗證頻率原則,我們采用了降維和濾波的辦法。一系列的實驗都驗證了頻率原則是一個廣泛存在的現象。
為什么會有頻率原則呢??事實上,在自然界中大部分信號都有一個特征,強度隨頻率增加而衰減。一般我們見到的函數在頻率空間也都有衰減的特征,特別是函數越光滑,衰減越快,連常見的ReLU函數在頻率空間也是關于頻率二次方衰減。在梯度下降的計算中,很容易得到低頻信號對梯度的貢獻要大于高頻,所以梯度下降自然就以消除低頻誤差為主要目標[2]。對于一般的網絡,我們有定性的理論證明[6],而對于線性NTK區域的網絡,我們有嚴格的線性頻率原則模型揭示頻率衰減的機制[7, 8, 9]。有了這個理解,我們也可以構造一些例子來加速高頻的收斂,比如在損失函數中增加輸出關于輸入的導數項,因為求導在頻率空間看,相當于在強度上乘以了一個其對應的頻率,可以緩解高頻的困難。這在求解PDE中很常見。
了解頻率原則對我們理解神經網絡有什么幫助嗎??我們舉兩個例子。第一個是理解提前停止這個技巧。實際的訓練中,一般都能發現泛化最好的點并不是訓練誤差最低的,通常需要在訓練誤差還沒降得很低的時候,提前停止訓練。實際數據大部分都是低頻占優,而且基本都有噪音。噪音對低頻的影響相對比較小,而對高頻影響相對比較大,而神經網絡在學習過程先學習低頻,所以通過提前停止可以避免學習到過多被污染的高頻而帶來更好的泛化性能。另一個例子是,我們發現圖像分類問題中,從圖像到類別的映射通常也是低頻占優,所以可以理解其良好的泛化。但對于定義在d維空間中的奇偶函數,其每一維的值只能取1或者-1。顯然任何一維被擾動后,輸出都會發生大的變化。這個函數可以被證明是高頻占優的,而實際訓練中,神經網絡在這個問題中完全沒有預測能力。我們還利用頻率原則解釋了為什么在實驗中會觀察到深度可以加快訓練,核心的原因是越深的網絡把目標函數變成一個越低頻的函數,使學習變得容易 [10]。
除了理解,頻率原則能對我們實際設計和使用神經網絡產生什么指導嗎?頻率原則揭示了神經網絡中存在高頻災難,這也引起了很多研究人員的注意,包括求解PDE、生成圖像、擬合函數等。高頻災難帶來的訓練和泛化困難很難通過簡單的調參來緩解。我們組提出了多尺度神經網絡的方法來加速高頻的收斂[11]。基本的想法是把目標函數在徑向進行不同尺度的拉伸,嘗試將不同頻率的成分都拉伸成一致的低頻,達到一致的快速收斂。實現也是非常之容易,僅需在第一隱藏層的神經元的輸入乘以一些固定的系數即可。我們的一些工作發現調整激活函數對網絡的性能影響很大[12],用正弦余弦函數做第一個隱藏層的基可以有比較好的效果[13]。這個算法被華為的MindSpore所采用。徑向拉伸的想法在很多其它的算法中也被采用,包括在圖片渲染中非常出名的NerF(神經輻射場)。
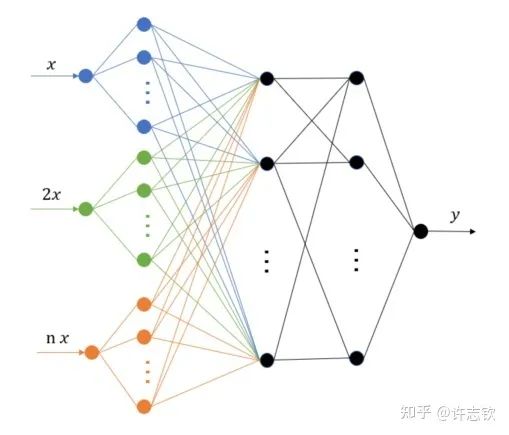 多尺度網絡結構
多尺度網絡結構
頻率原則還有很多未解的問題需要被探索。?在非梯度下降訓練的過程,比如粒子群算法怎么證明頻率下降[14]?如何在理論上論證多尺度神經網絡對高頻的加速效果?是否有更穩定更快的高頻加速算法?小波可以更細致的描述不同局部的頻率特征,能否用小波更細節地理解神經網絡的訓練行為?數據量、網絡深度、損失函數怎么影響頻率原則?頻率原則可以指導算法設計的理論,為訓練規律提供一種“宏觀”描述。對于“微觀”機制,我們需要進一步研究。同樣是低頻到高頻的學習過程,參數的演化可以非常不一樣,比如一個函數可以用一個神經元表示,也可以用10個神經元(每個神經元的輸出權重為原輸出權重的1/10)一起表示,從輸入輸出函數的頻率來看,這兩種表示完全沒有差別,那神經網絡會選擇哪一種表示,以及這些表示有什么差別?下面我們就要更細致地看參數演化中的現象。
參數凝聚現象
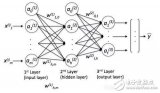
為了介紹參數凝聚現象我們有必要介紹一下兩層神經元網絡的表達
W是輸入權重,它以內積的方式提取輸入在權重所在的方向上的成分,可以理解為一種特征提取的方式,加上偏置項,然后再經過非線性函數(也稱為激活函數),完成單個神經元的計算,然后再把所有神經元的輸出加權求和。為了方便,我們記
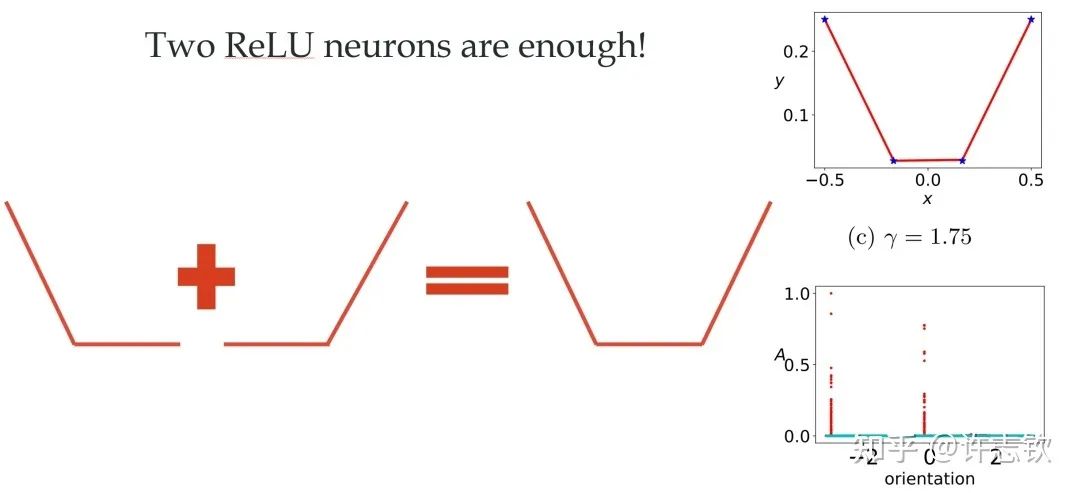
對于ReLU激活函數,我們可以通過考慮輸入權重的角度和神經元的幅度來理解每個神經元的特征:, 其中?。考慮用上面的兩層神經網絡來擬合四個一維的數據點。結合輸入權重和偏置項,我們所關心的方向就是兩維的方向,因此可以用角度來表示其方向。下圖展示了,不同初始化下,神經網絡的擬合結果(第一行),以及在訓練前(青色)和訓練后(紅色)特征分布的圖(第二行)
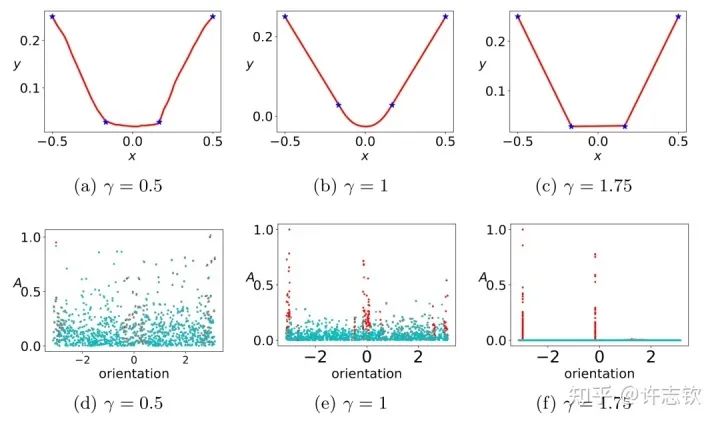 不同初始化的擬合結果
不同初始化的擬合結果
顯然,隨初始化尺度變小(從左到右,初始化尺度不斷變小),神經網絡的擬合結果差異很大,在特征分布上,當尺度很大(這里使用NTK的初始化),神經網絡特征幾乎不變,和random feature這類線性模型差不多,而隨初始化變小,訓練過程出現明顯的特征變化的過程。最有意思的是,這些特征的方向聚集在兩個主要的方向。我們把這種現象稱為參數凝聚。?大量的實際問題告訴我們神經網絡比線性的方法要好很多,那非線性過程所呈現的參數凝聚有什么好處嗎??如下圖展示的一個極端凝聚的例子,對于一個隨機初始化的網絡,經過短暫的訓練后,每個隱藏層神經元的輸入權重是完全一致的,因此這個網絡可以等效成僅有一個隱藏層神經元的小網絡。一般情況下,神經元會凝聚到多個方向。
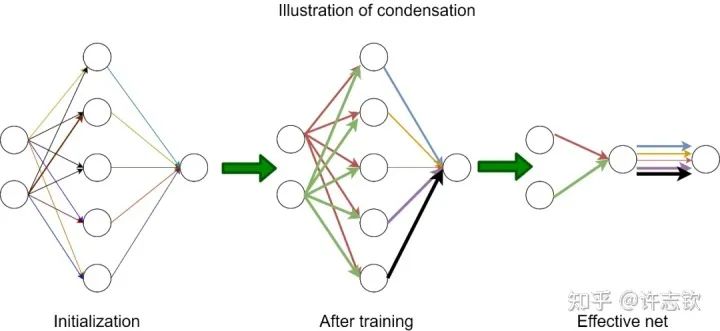 凝聚現象的例子
凝聚現象的例子
回顧在我們前面最開始提到的泛化迷團,以及我們最開始提出的問題“在實際訓練中,神經網絡真的很復雜嗎?”,在參數凝聚的情況下,對于一個表面看起來很多參數的網絡,我們自然要問:神經網絡實際的有效參數有多少??比如我們前面看到的兩層神經網絡凝聚在兩個方向的例子,實際上,這個網絡的有效神經元只有兩個。因此凝聚可以根據實際數據擬合的需求來有效地控制模型的復雜度。
前面,我們只是通過一個簡單的例子來呈現凝聚現象,接下來重要的問題是:參數凝聚是非線性過程中普遍的現象嗎??在統計力學相圖的啟發下,我們在實驗發現并理論推導出了兩層無限寬ReLU神經網絡的相圖。基于不同的初始化尺度,以參數在訓練前后的相對距離在無限寬極限下趨于零、常數、無窮作為判據,相圖劃分了線性、臨界、凝聚三種動力學態(dynamical regime)。領域內的一系列理論研究(包括NTK,mean-field等)都可以在我們的相圖中找到對應的位置[3]。
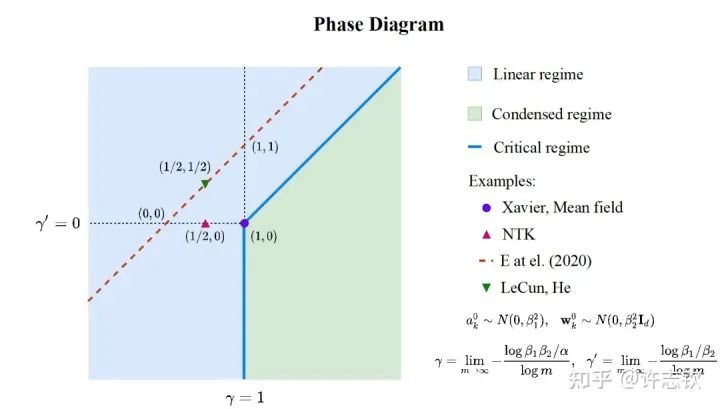 兩層ReLU網絡的相圖
兩層ReLU網絡的相圖
在三層無窮寬[15]的全連接網絡中,我們實驗證明在所有非線性的區域,參數凝聚都是一種普遍的現象。理論上,我們證明當初始化尺度足夠小的時候,在訓練初始階段就會產生凝聚[4] 。有趣的是,我們在研究Dropout算法的隱式正則化的時候,發現Dropout算法會明顯地促進參數凝聚地形成。?Dropout算法的想法是Hinton提出的,在神經網絡的訓練中,以一定概率p保留神經元,是一種常用的技巧,對泛化能力的提升有明顯的幫助。我們首先來看一下擬合結果。下面左圖是沒有用Dropout的例子,放大擬合的函數,可以看到明顯的小尺度的波動,右圖是用了Dropout的結果,擬合的函數要光滑很多。
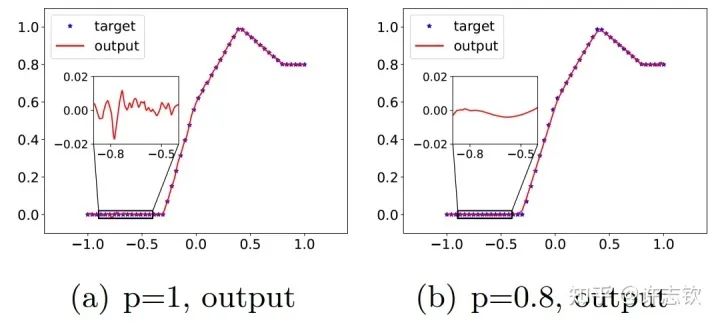 Dropout(右)使輸出更光滑
Dropout(右)使輸出更光滑
仔細看他們的特征分布時,可以看到訓練前(藍色)和訓練后(橙色)的分布在有Dropout的情況下會明顯不同,且呈現出明顯地凝聚效應,有效參數變得更少,函數復雜度也相應變得簡單光滑。
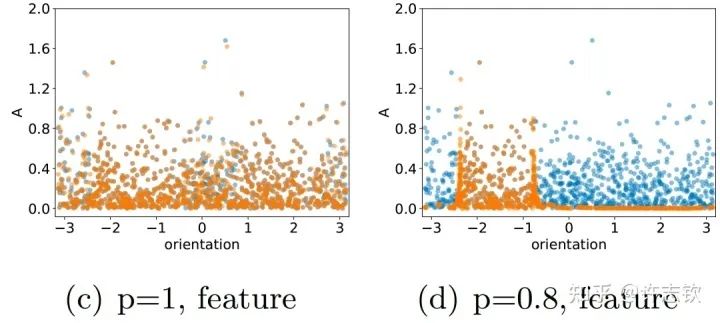 Dropout(右)使參數凝聚
Dropout(右)使參數凝聚
進一步,我們分析為什么Dropout會帶來凝聚效應。我們發現Dropout的訓練會帶來一項特殊的隱式正則效應。我們通過下面的例子來理解這個效應。下面黃色和紅色兩種情況都能合成一個相同的向量,Dropout要求兩個分向量的模長平方和要最小,那顯然只有當兩個向量的方向一致的時候,并且完全相等的時候,它們的模長平方和才能最小,對于w來說,這就是凝聚。

到目前,我們談了參數凝聚使得神經網絡的有效規模變得很小,那為什么我們不直接訓練一個小規模的網絡?大網絡和小網絡有什么差異??首先,我們用不同寬度的兩層網絡來擬合同一批數據,下圖展示了它們的損失下降的過程。
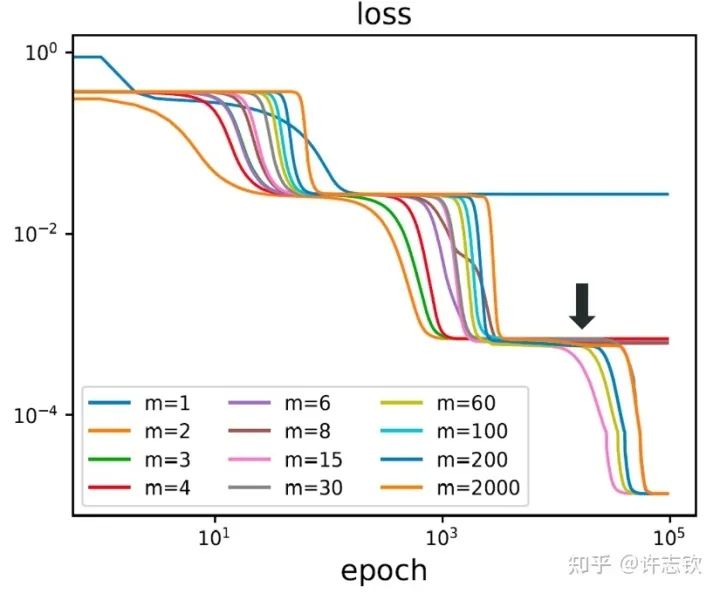
不同寬度的網絡的損失函數表現出了高度的相似性,它們會在共同的位置發生停留。那在共同的臺階處有什么相似性呢?下面左圖可以看到,對于上述箭頭指示的臺階,不同寬度網絡的輸出函數非常靠近。更進一步看它們的特征圖(下右圖),它們都發生了強烈的凝聚現象。這些體現了它們的相似性。
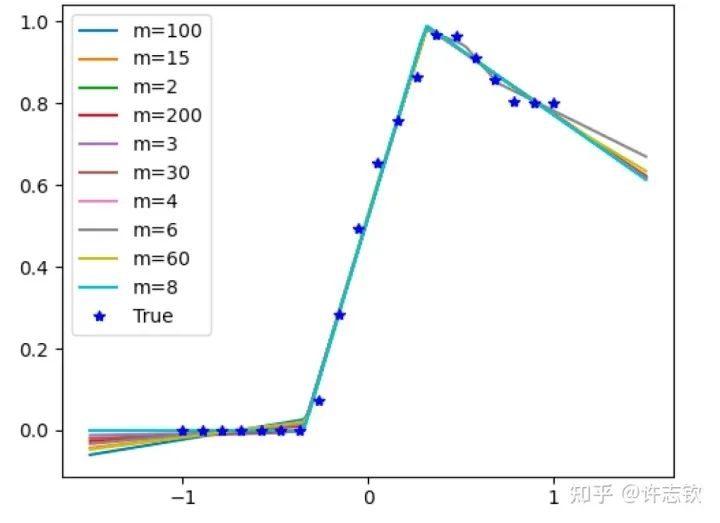
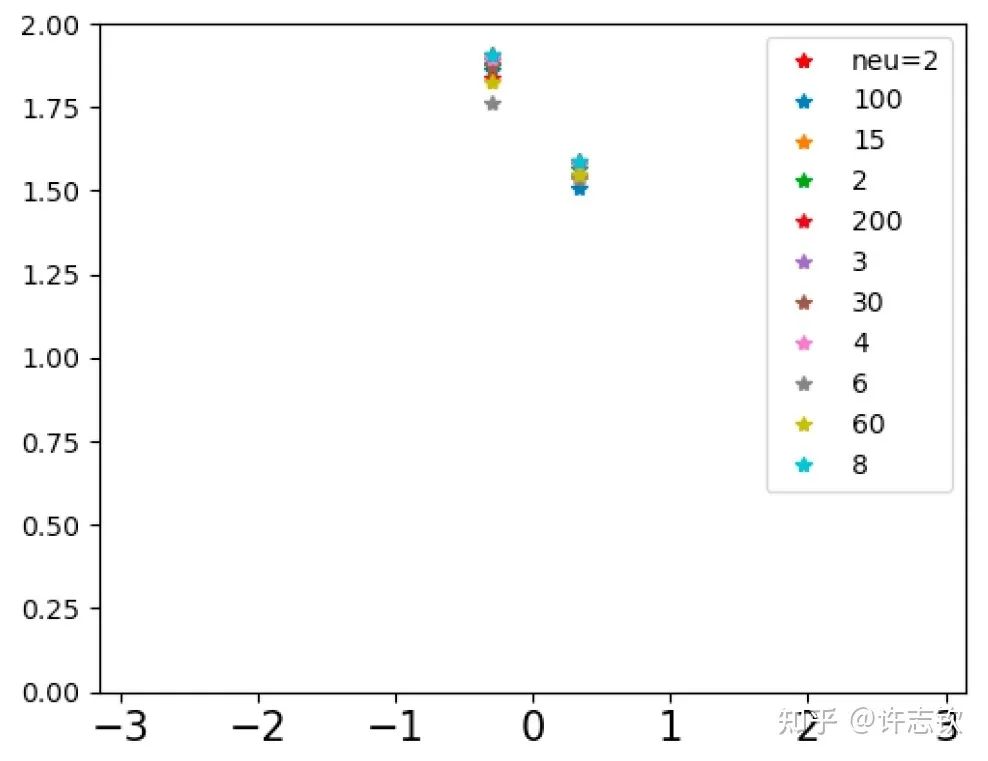
如果再仔細觀察他們的損失圖,可以發現當寬度增加的時候,網絡的損失函數更容易下降,比如前面箭頭指的地方,相對小的網絡就停留在臺階上,大的網絡的損失才繼續下降。從實驗上可以看出,大網絡凝聚時雖然和小網絡在表達能力類似,但看起來大網絡更容易訓練。怎么解釋不同寬度的網絡的相似性以及大網絡的優勢??在一個梯度下降的訓練過程,出現平臺的原因很可能是因為訓練路徑經歷某個鞍點(附近有上升方向也有下降方向的極值點)附近。不同寬度的網絡似乎會經歷相同的鞍點。但參數量不同的網絡,它們各自的鞍點生活在不同維度的空間,怎么會是同一點呢?
我們證明了不同寬度的網絡的損失景觀的極值點存在一個嵌入原則(Embedding Principle)[16], 即一個神經網絡的損失景觀中 “包含”所有更窄神經網絡損失景觀的所有臨界點(包括鞍點、局部最優點和全局最優點等)。簡單地說,就是一個網絡處理臨界點時,通過一些特定的嵌入方式,可以把這個網絡嵌入到一個更寬的網絡中,嵌入過程能夠保持網絡輸出不變以及寬網絡仍然處于臨界點。最簡單的嵌入方式正是凝聚的逆過程,比如下圖是一種一步嵌入方式。更一般的嵌入方式我們在Journal of Machine Learning第一期的文章里[17]有詳細討論。
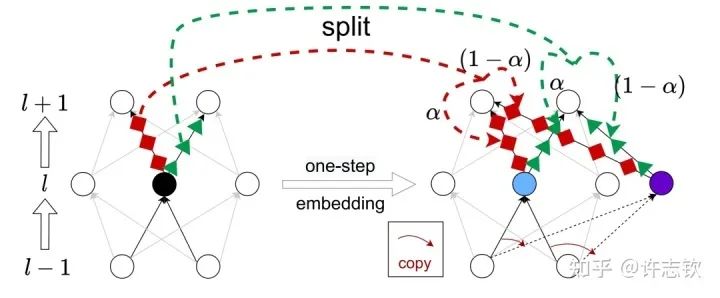
嵌入原則揭示了不同寬度網絡的相似性,當然也提供了研究它們差異性的手段。由于在嵌入的過程中有自由參數,因此在更大網絡的臨界點的退化程度越大。同樣的,一個大網絡的損失景觀里的臨界點,如果它來源于更簡單的網絡的臨界點的嵌入,那么它的退化程度也越大(直觀可以理解它占的空間越大)。我們就可以猜測這些越簡單的臨界點越有可能被學習到。
另外,我們在理論上證明,在嵌入的過程中,臨界點附近的下降方向、上升方向都不會變少。這告訴我們,一個鞍點被嵌入到一個更大的網絡以后,它不可能變成一個極小值點,但一個極小值點被嵌入到大網絡以后,它很有可能會變成鞍點,產生更多的下降方向。我們在實驗上也證明了嵌入過程會產生更多下降方向。
因此,我們有理由相信,大網絡盡管凝聚成有效的小網絡,但它會比小網絡更容易訓練。也就是大網絡既可以控制模型的復雜度(可能帶來更好的泛化),又可以使訓練更容易。?我們的工作還發現了在深度上神經網絡損失景觀的嵌入原則[18]。關于凝聚現象,同樣還有很多問題值得繼續深入。下面是一些例子。除了初始訓練外,訓練過程中的凝聚現象產生的機制是什么?不同的網絡結構是否有凝聚現象?凝聚的過程和頻率原則有什么聯系?凝聚怎么定量地和泛化建立聯系?
總結
過去五年,在深度學習的基礎研究方面,我們主要圍繞頻率原則和參數凝聚兩類現象展開工作。從發現它們,意識到他們很有趣,再到解釋它們,并在一定程度上基于這些工作去理解深度學習的其它方面和設計更好的算法。未來五年,我們將在深度學習的基礎研究和AI for Science方面深入鉆研。
參考文獻
[1] Zhi-Qin John Xu*, Yaoyu Zhang, and Yanyang Xiao, Training behavior of deep neural network in frequency domain, arXiv preprint: 1807.01251, (2018), ICONIP 2019.
[2] Zhi-Qin John Xu* , Yaoyu Zhang, Tao Luo, Yanyang Xiao, Zheng Ma, Frequency Principle: Fourier Analysis Sheds Light on Deep Neural Networks, arXiv preprint: 1901.06523, Communications in Computational Physics (CiCP).
[3]Tao Luo#,Zhi-Qin John Xu #, Zheng Ma, Yaoyu Zhang*, Phase diagram for two-layer ReLU neural networks at infinite-width limit, arxiv 2007.07497 (2020), Journal of Machine Learning Research (2021)
[4]Hanxu Zhou, Qixuan Zhou, Tao Luo, Yaoyu Zhang*, Zhi-Qin John Xu*, Towards Understanding the Condensation of Neural Networks at Initial Training. arxiv 2105.11686 (2021), NeurIPS2022.
[5] Jihong Wang,Zhi-Qin John Xu*, Jiwei Zhang*, Yaoyu Zhang, Implicit bias in understanding deep learning for solving PDEs beyond Ritz-Galerkin method, CSIAM Trans. Appl. Math.
[6] Tao Luo, Zheng Ma,Zhi-Qin John Xu, Yaoyu Zhang, Theory of the frequency principle for general deep neural networks, CSIAM Trans. Appl. Math., arXiv preprint, 1906.09235 (2019).
[7] Yaoyu Zhang, Tao Luo, Zheng Ma,Zhi-Qin John Xu*, Linear Frequency Principle Model to Understand the Absence of Overfitting in Neural Networks. Chinese Physics Letters, 2021.
[8] Tao Luo*, Zheng Ma,Zhi-Qin John Xu, Yaoyu Zhang, On the exact computation of linear frequency principle dynamics and its generalization, SIAM Journal on Mathematics of Data Science (SIMODS) to appear, arxiv 2010.08153 (2020).
[9]Tao Luo*, Zheng Ma, Zhiwei Wang, Zhi-Qin John Xu, Yaoyu Zhang, An Upper Limit of Decaying Rate with Respect to Frequency in Deep Neural Network, To appear in Mathematical and Scientific Machine Learning 2022 (MSML22),
[10] Zhi-Qin John Xu* , Hanxu Zhou, Deep frequency principle towards understanding why deeper learning is faster, AAAI 2021, arxiv 2007.14313 (2020)
[11] Ziqi Liu, Wei Cai,Zhi-Qin John Xu* , Multi-scale Deep Neural Network (MscaleDNN) for Solving Poisson-Boltzmann Equation in Complex Domains, arxiv 2007.11207 (2020) Communications in Computational Physics (CiCP).
[12] Xi-An Li,Zhi-Qin John Xu* , Lei Zhang, A multi-scale DNN algorithm for nonlinear elliptic equations with multiple scales, arxiv 2009.14597, (2020) Communications in Computational Physics (CiCP).
[13] Xi-An Li,Zhi-Qin John Xu, Lei Zhang*, Subspace Decomposition based DNN algorithm for elliptic type multi-scale PDEs. arxiv 2112.06660 (2021)
[14]Yuheng Ma,Zhi-Qin John Xu*, Jiwei Zhang*, Frequency Principle in Deep Learning Beyond Gradient-descent-based Training, arxiv 2101.00747 (2021).
[15]Hanxu Zhou, Qixuan Zhou, Zhenyuan Jin, Tao Luo, Yaoyu Zhang,Zhi-Qin John Xu*, Empirical Phase Diagram for Three-layer Neural Networks with Infinite Width. arxiv 2205.12101 (2022), NeurIPS2022.
[16]Yaoyu Zhang*, Zhongwang Zhang, Tao Luo,Zhi-Qin John Xu*, Embedding Principle of Loss Landscape of Deep Neural Networks. NeurIPS 2021 spotlight, arxiv 2105.14573 (2021)
[17] Zhongwang Zhang,Zhi-Qin John Xu*, Implicit regularization of dropout. arxiv 2207.05952 (2022)
[18]Zhiwei Bai, Tao Luo,Zhi-Qin John Xu*, Yaoyu Zhang*, Embedding Principle in Depth for the Loss Landscape Analysis of Deep Neural Networks. arxiv 2205.13283 (2022)
編輯:黃飛
?
 電子發燒友App
電子發燒友App












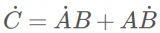





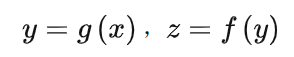












評論