數字濾波器原理
數字濾波器主要由數字乘法器、加法器、延時電路等部分構成,其實就是一個數字信號處理器,主要使用數字計算機對數字信號按照預先編制的程序進行相應的計算。若采用通用的計算機,隨時編寫程序就可以完成對信號的處理,但速度較慢;若采用專用的計算機,其芯片是根據固定的計算方法制成的一種集成電路,連接信號后就可以完成對信號的處理,速度較快,但處理方式無法更改;若采用可編程的計算機芯片,則既可以編寫不同程序以達到處理方式的多樣化,又具有較快的處理速度,因此是目前市場內應用最為廣泛的。
數字濾波器對模擬信號進行濾波時的步驟如下圖所示,首先經過模數轉換器將待處理的模擬信號轉換為數字信號,再經數字信號處理器對待處理的數字信號進行處理,最后經數模轉換器將處理過的數字信號轉換為模擬信號,至此,完成了對模擬信號的處理。我們可以這樣來理解數字濾波器,它是一種通過對數字信號進行處理來完成對數字信號或者模擬信號進行濾波的儀器。

數字濾波器分類
濾波器根據功能的不同可分為低通濾波器、高通濾波器、帶通濾波器和帶阻濾波器四種;根據實現方法的不同可分為FIR濾波器和IIR濾波器兩種;根據設計方法的不同可分為切比雪夫濾波器和巴特沃斯濾波器;根據處理信號的不同可分為經典濾波器和現代濾波器兩種;根據處理信號的不同可以分為數字濾波器和模擬濾波器。數字濾波器是濾波器的一種,但以上分類都是獨立的,因此數字濾波器也具有以上幾種分類形式。
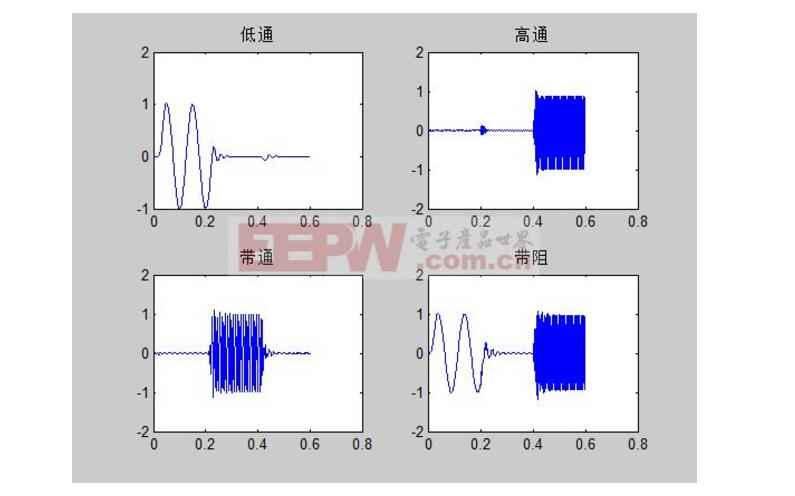
數字濾波器的設計方法及步驟
一、模擬低通濾波器的設計方法
⑴確定階次N
①已知Ωc、Ωs和As求ButterworthDF階數N
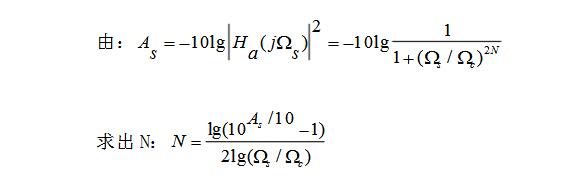
②已知Ωc、Ωs和Ω=Ωp的衰減Ap求ButterworthDF階數N
得到N: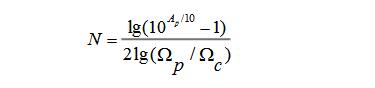
③已知Ωp、Ωs和Ω=Ωp的衰減Ap和As求ButterworthDF階數N
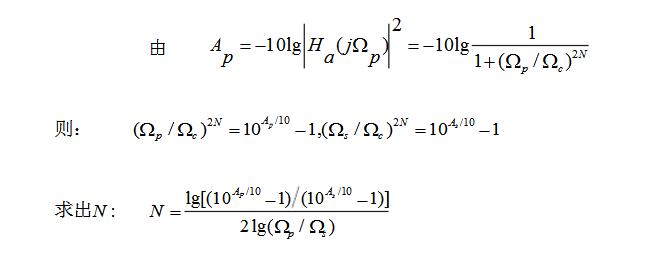
⑵用階次N確定Ha(s)
根據公式:
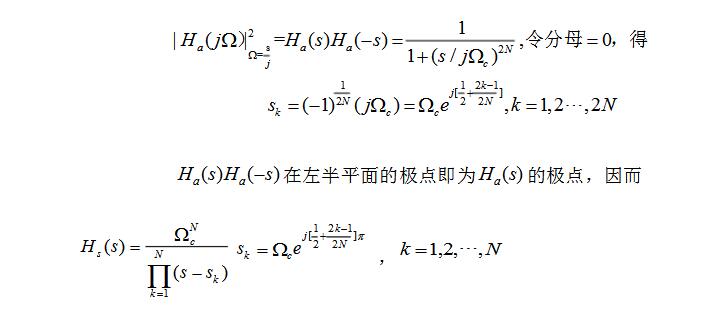
2、切比雪夫低通濾波器設計步驟:
⑴確定技術指標Ωp,ap,Ωs,as
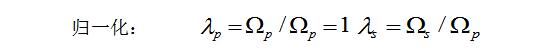
⑵根據技術指標求出濾波器階數N及
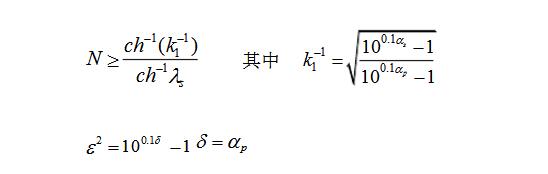
⑶求出歸一化系統函數其中極點由下式求出:
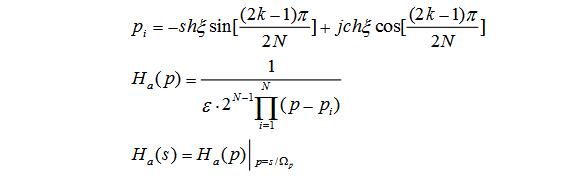
或者由N和S直接查表得Ha(p)
⑷去歸一化: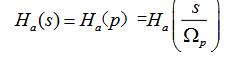
二、數字低通濾波器的設計步驟:
1、確定數字低通濾波器的技術指標:通帶截止頻率、通帶最大衰減系數
阻帶截止頻率、阻帶最小衰減系數。
2、將數字低通濾波器的技術指標轉換成模擬低通濾波器的技術指標。巴特沃斯

3、把模擬濾波器變換成數字濾波器,即把模擬濾波器的系數映射成數字濾波器的系統函數。
實現系統傳遞函數s域至z域映射有脈沖響應不變法和雙線性映射兩種方法。
(1)脈沖響應不變法。
按照技術要求設計一個模擬低通濾波器,得到模擬低通濾波器的傳輸函數轉換成數字低通濾波器的系統函數H(z)。

對上式進行Z變換,得到數字濾波器的系統函數H(z)
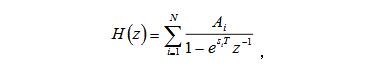
經過一系列變換得到:
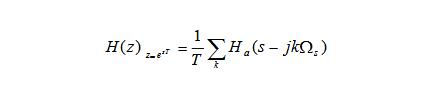
(2)雙線性變換法
這種變換方法,采用非線性頻率壓縮方法,將整個頻率軸上的頻率范圍壓縮到±π/T之間,再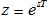 轉換到z平面上。設Ha(s),s=jΩ,經過非線性頻率壓縮后用Ha(s1),表示,這里用正切變換實現頻率壓縮:
轉換到z平面上。設Ha(s),s=jΩ,經過非線性頻率壓縮后用Ha(s1),表示,這里用正切變換實現頻率壓縮:
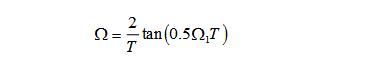
式中T仍是采樣間隔,當Ω1從-π/T經過0變化到π/T時,Ω則由-∞經過0變化到+∞,實現了s平面上整個虛軸完全壓縮到s1平面上虛軸的±π/T之間的轉換。這樣便有

兩種方法比較:
脈沖響應不變法的優點:
1,模擬頻率到數字頻率的轉換時線性的;
2,數字濾波器單位脈沖響應的數字表示近似原型的模擬濾波器單位脈沖響應,因此時域特性逼近好。
缺點:
會產生頻譜混疊現象,只適合帶限濾波器雙線性變換法優點:
克服多值映射得關系,可以消除頻率的混疊
缺點:
時域到頻域的變換是非線性的,在高頻處有較大的失真。
三、數字高通濾波器的設計步驟:
①數字高通濾波器的技術指標為:通帶截止頻率ωp阻帶截止頻率ωs通帶衰減頻率αP阻帶衰減頻率αs
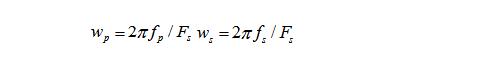
②預畸變處理,將數字高通指標轉換為模擬低通指標
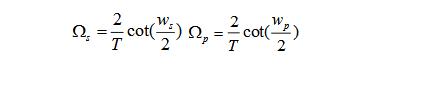
③確定階數N由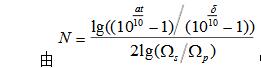 (可由模擬低通濾波器設計方法可得
(可由模擬低通濾波器設計方法可得
④歸一化及去歸一化查表令s=s/Ω歸一化模擬低通圓型系統函數
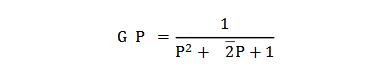
⑤低通向高通轉化令s1=1/s由頻率變換公式

⑥濾波器數字化令利用雙線性變換化
數字高通不能采用脈沖響應不變法原因是:脈沖響應不變法有頻譜周期延拓效應,因此只能用于帶限的頻響特性,如衰減特性很好的低通或帶通。而高頻衰減越大,頻響的混淆效應越小,至于高通濾波器,由于它們在高頻部分不衰減,因此將完全混淆在低頻響應中。
四、數字帶通濾波器的設計:
步驟:
(1)確定性能指標:在設計帶通濾波器之前,首先根據工程實際的需要確定濾
波器的技術指標:通帶截止頻率wc1,wc2、阻帶截止頻率wr1,wr2、阻帶最小衰減αs通帶最大衰減αp
(2)對帶通數字濾波器H(z)的數字邊界頻率預畸變
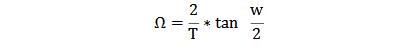
得到帶通模擬濾波器H(s)的邊界頻率
主要是通帶截止頻率ωp1,ωp2;阻帶截止頻率ωs1,ωs2的轉換。
對雙線性變換法一般T=2s
通帶截止頻率wc1=(2/T)*tan(wp1/2)、wc2=(2/T)*tan(wp2/2)
阻帶截止頻率wr1=(2/T)*tan(ws1/2)、wr2=(2/T)*tan(ws2/2)
阻帶最小衰減αs通帶最大衰減αp
(3)低通到帶通頻率變換
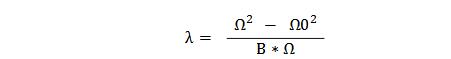
將模擬帶通濾波器指標轉換為模擬低通濾波器指標。
B=wc2-wc1
normwr1=(((wr1^2)-(w0^2))/(B*wr1))
normwr2=(((wr2^2)-(w0^2))/(B*wr2))
normwc1=(((wc1^2)-(w0^2))/(B*wc1))
normwc2=(((wc2^2)-(w0^2))/(B*wc2))
模擬低通濾波器指標:
normwc,normwr,αp,αs
(4)設計模擬低通原型濾波器。查表得到歸一化低通傳輸函數G(p):
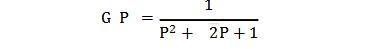
用模擬低通濾波器設計方法(由巴特沃斯設計步驟或切比雪夫設計步驟)得到模擬低通濾波器的傳輸函數Ha(s)
(5)模擬低通濾波器轉化為模擬帶通濾波器。
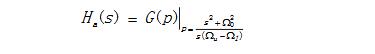
(6)利用雙線性變換法將模擬帶通濾波器Ha(s)轉換成數字帶通濾波器H(z)
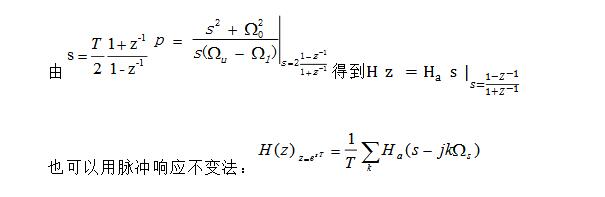
兩種方法比較比較:
脈沖響應不變法數字濾波器單位脈沖響應的數字表示近似原型的模擬濾波器單位脈沖響應,因此時域特性逼近好。但會產生頻譜混疊現象,只適合帶限濾波器雙線性變換法可以克服多值映射得關系,可以消除頻率的混疊但時域到頻域的變換是非線性的,在高頻處有較大的失真。
五、數字帶阻濾波器的設計:
步驟:
(1)確定性能指標:
通帶截止頻率wc1,wc2、阻帶截止頻率wr1,wr2、阻帶最小衰減αs通帶最大衰減αp
(2)對帶通數字濾波器H(z)的數字邊界頻率預畸變
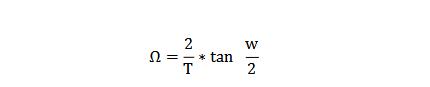
主要是通帶截止頻率ωp1,ωp2;阻帶截止頻率ωs1,ωs2的轉換。
對雙線性變換法一般T=2s
通帶截止頻率wc1=(2/T)*tan(wp1/2)、wc2=(2/T)*tan(wp2/2)
阻帶截止頻率wr1=(2/T)*tan(ws1/2)、wr2=(2/T)*tan(ws2/2)
阻帶最小衰減αs通帶最大衰減αp
(由模擬低通濾波器設計方法可得
模擬低通濾波器確定模擬帶阻濾波器
由模擬低通到模擬帶阻的變換這一模擬低通到帶阻的變換關系為


數字帶阻濾波器不能用脈沖響應不變法:原因是脈沖響應不變法有頻譜周期延拓效應,因此只能用于帶限的頻響特性,如衰減特性很好的低通或帶通。而高頻衰減越大,頻響的混淆效應越小,至于帶阻濾波器,由于它們在高頻部分不衰減,因此將完全混淆在低頻響應中。
 電子發燒友App
電子發燒友App










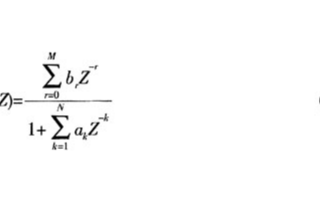

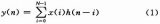












評論