自1971年以來,兩位數(shù)學科學家猜測,超級大整數(shù)相乘極限速度將是N log (N),且無法被超越。近日,該猜測終于被實現(xiàn):2個10億位超級大整數(shù)相乘,僅需30秒!
超級大整數(shù)相乘極限速度實現(xiàn)了!
整數(shù)相乘是每個人必學的一個運算,我們通常采用的思路是:第一個數(shù)字的n位乘以第二個數(shù)字的n位,這就意味著要進行n2次的乘法運算。但當這兩個整數(shù)大到一定程度時,這個過程的計算量是相當龐大且驚人的。
當然,前人們已經(jīng)找到了一些解決方法來改善這一問題。早在1971年,兩位德國數(shù)學家就猜測,兩個大數(shù)相乘的可以達到一種令人難以置信的速度,即N log (N)。然而,這個聰明的想法幾十年來一直只是假設。
直到現(xiàn)在,這個假設終于被證明了!
澳大利亞新南威爾士大學(UNSW)的數(shù)學家、副教授David Harvey近日聲稱,他和他的合著者首次破解了這個由Arnold Sch?nhage 和 Volker Strassen提出,存在近半個世紀之久的數(shù)學難題。
論文地址:
https://hal.archives-ouvertes.fr/hal-02070778/document
簡單來說,這項研究采用了1,729維快速傅里葉變換(FFT),使得計算速度達到了N log (N)——目前理論上的極限值。
以前,兩個十億位的整數(shù)相乘,若是采用常規(guī)算法,大約需要幾個月才能算出它們的結果。但是應用該新算法,僅需30秒!
數(shù)學處處充滿驚喜,大數(shù)乘法速度屢破記錄,或已至極限
兩個整數(shù)相乘很簡單對吧?
小學的時候我們就學過如何做整數(shù)的乘法運算,例如:
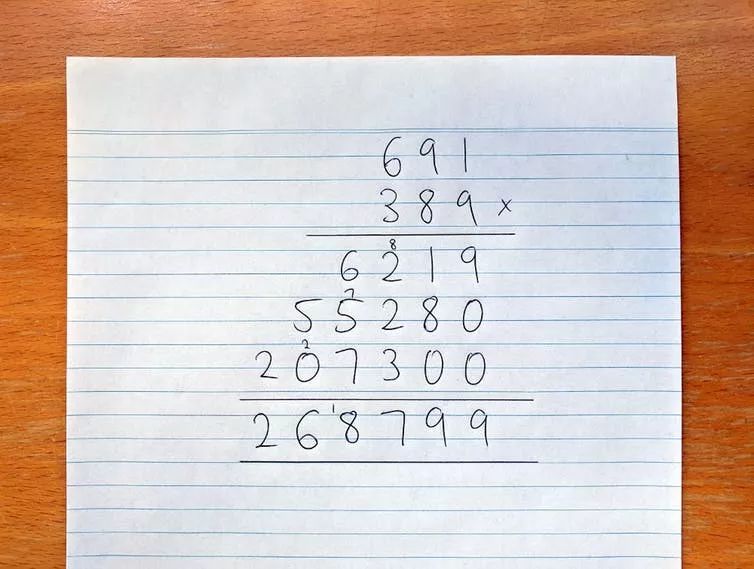
但是,若是整數(shù)長度大到了一定程度,這種方法真的是最好的嗎?
在一般的乘法運算過程中,我們需要把第一個整數(shù)的每一位和第二個整數(shù)的每一位做乘法。如果這兩個數(shù)都有N位,那就是N2(或N x N)相乘。在上面的例子中,N是3,所以我們要做32 = 9次乘法。
1956年前后,著名的蘇聯(lián)數(shù)學家安德烈·科爾莫戈羅夫(Andrey Kolmogorov)推測,這就是兩個整數(shù)相乘的最好方法。
換句話說,不管你怎么安排計算,你要做的功至少與N2成正比。兩倍的數(shù)字意味著四倍的工作量。
科爾莫戈羅夫認為,如果有更簡便的方法,那肯定已經(jīng)人們發(fā)現(xiàn)了,畢竟人類在“乘法”這件事兒上探索了千年之久。
被打臉,更快的方法誕生
然而,就在幾年后,科爾莫戈羅夫就被打臉了。
1960年,23歲的俄羅斯數(shù)學系學生阿納托利·卡拉蘇巴(Anatoly Karatsuba)發(fā)現(xiàn)了一種代數(shù)技巧,可以減少所需的乘法次數(shù)。
例如,要乘四位數(shù)的數(shù),不需要42 = 16的乘法,卡拉蘇巴的方法只需要9次。當使用他的方法時,兩倍的數(shù)字只意味著三倍的工作量。
而且隨著數(shù)字位數(shù)的增大,這種方法的有效性越發(fā)顯著,對于一千位數(shù)字的相乘,比之前的方法所需的乘法次數(shù)要少17倍。
大數(shù)字相乘在生活中的應用
有人會很好奇,誰會用到這么大的數(shù)字來做乘法呢?事實上,現(xiàn)實生活中由大量的應用是需要這么做的,最典型的就是密碼學。
每次我們在互聯(lián)網(wǎng)上進行加密通信時(例如,訪問銀行網(wǎng)站或執(zhí)行網(wǎng)絡搜索),我們的設備都會執(zhí)行的乘法次數(shù)是非常恐怖的,涉及數(shù)百甚至數(shù)千位的數(shù)字。
對于一些更深奧的應用程序,數(shù)學家必須處理更大的數(shù)字,數(shù)百萬、數(shù)十億甚至數(shù)萬億的數(shù)字。對于如此龐大的數(shù)字,即使是卡拉蘇巴的算法也是太慢了。
1971年,德國數(shù)學家阿諾德·紹哈格(Arnold Schonhage)和沃爾克·斯特拉森(Volker Strassen)的工作取得了真正的突破。他們解釋了如何使用快速傅里葉變換(FFT)來有效地對“大數(shù)字”做乘法。今天的數(shù)學家經(jīng)常使用他們的方法來處理數(shù)十億位數(shù)的數(shù)字。
極限速度猜測
在他們1971年發(fā)表的論文中,他們也提到了一個驚人的猜測。
他們猜測的前半部分是,應該有可能使用最多與N log (N) (N乘以N的自然對數(shù))成比例的一些基本運算來乘N位數(shù)字。但他們的算法并沒有達到這個理想的結果,速度慢了一個log因子(log N)。
而后的研究者們對此進行了不懈的深入挖掘,但直到2007年,Martin Furer的工作也只是接近N log (N)。
猜測的后半部分是,N log (N)應該就是速度的極限——沒有任何可能的乘法算法能做得比這個更好。
乘法運算速度極限已經(jīng)實現(xiàn)?
就在前幾周,Joris van der Hoeven和David Harvey共同發(fā)表的一篇論文《Integer multiplication in time O(n log n)》描述了一種新的乘法算法,最終達到了N log(N)這一“圣杯”。
該算法突破性重點在于使用多維FFT,而不是僅僅使用一維FFT。自1971年以來,在很多領域都會涉及多維FFT的應用,例如JPEG格式圖像依賴于二維FFT,而三維FFT在物理和工程中有很多應用。
而在這篇論文中,所用到的FFT維度高達1,729。
但是,以目前的形式來看,新算法實際上并不實用,因為論文中給出的證明只適用于非常大的數(shù)字。即使每個數(shù)字都寫在氫原子上,在可觀測的宇宙中也幾乎沒有足夠的空間把它們寫下來。
另一方面,作者還希望通過進一步的改進,使得該算法可以應用于只有數(shù)十億或數(shù)萬億位數(shù)的數(shù)字。如果是這樣,它很可能成為計算數(shù)學家“軍火庫”中不可或缺的工具。
若Schonhage-Strassen猜想是正確的,那么從理論的角度來看,新算法就是這條路的終點——不可能做得更好。
但論文作者也表示:“若猜想被證明是錯誤的,我會感到非常驚訝。但我們不應該忘記科爾莫戈羅夫的遭遇。”
畢竟,數(shù)學處處充滿驚喜。
作者簡介
David Harvey
新南威爾士大學數(shù)學與統(tǒng)計學院副教授和ARC未來研究員。研究領域包括計算數(shù)論與算術幾何,多項式與整數(shù)算術。
所獲獎項:
2017–2021: Counting points on algebraic surfaces ($805,054)ARC Future Fellowship, FT160100219
2015–2017: Fast algorithms for zeta functions of algebraic varieties ($325,500)ARC Discovery Project, DP150101689
2012–2014: Counting solutions to equations over fields of large characteristic ($375,000)ARC Discovery Early Career Researcher Award, DE120101293
主頁地址:
https://web.maths.unsw.edu.au/~davidharvey/
Joris van der Hoeven
CNRS研究主任、MAX團隊組長。主要研究集中在漸近微積分和復分析的自動化,以及快速算法。
曾與Matthias Aschenbrenner合作共同出版了《漸近微分代數(shù)與變級數(shù)模型理論》一書,證明了漸近微分代數(shù)的量詞消去定理。另一個主要研究課題是具有特殊函數(shù)或更一般的微分方程解的復分析和計算的自動化。一方面,這導致了一些有趣的理論問題,如可計算性、零點測試、奇點等。另一方面,需要為多精度計算開發(fā)和實現(xiàn)快速、可靠和數(shù)值穩(wěn)定的算法。
-
算法
+關注
關注
23文章
4710瀏覽量
95405 -
傅里葉變換
+關注
關注
6文章
443瀏覽量
43151
原文標題:極限速度!10億位超級大整數(shù)相乘僅需30秒,半個世紀的猜測終被證明
文章出處:【微信號:AI_era,微信公眾號:新智元】歡迎添加關注!文章轉載請注明出處。
發(fā)布評論請先 登錄
GB10超級芯片開賣!正式殺入AI PC
Redis 8 向量搜索實測:輕松擴展至 10 億向量

請問一下是不是LMX2541只有輸入為整數(shù)時才能被鎖定
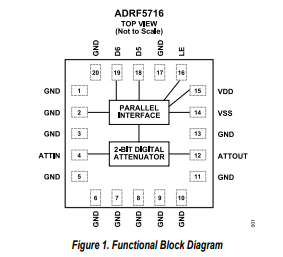
ADRF5716硅數(shù)字衰減器,2位,100MHz至30GHz技術手冊
AI 推理服務器都有什么?2025年服務器品牌排行TOP10與選購技巧

超級電容器均壓電路狀況與展望
TECS OpenStack資源池時間同步失敗的故障分析

2秒啟動!飛凌嵌入式RK3506開發(fā)板LVGL顯示方案,讓界面炫起來

億緯鋰能儲能超級工廠二期投產(chǎn),MB56電池引領大容量儲能新時代
一個DAC的最高采樣率是125MSPS,該DAC是14bit的,那么如果輸出2Mhz的正弦波信號,每個周期10個點,可以實現(xiàn)嗎?
DAC7750供電電源超過30V被燒毀,為什么?
RISC-V基本整數(shù)指令
鴻蒙原生應用元服務開發(fā)-倉頡基礎數(shù)據(jù)類型整數(shù)類型
RISC-V基礎整數(shù)指令集
ADS1204 4個1位、10MHz、2階、Δ-Σ調制器數(shù)據(jù)表






 該猜測終于被實現(xiàn):2個10億位超級大整數(shù)相乘,僅需30秒!
該猜測終于被實現(xiàn):2個10億位超級大整數(shù)相乘,僅需30秒!











評論